A Step Farther Out (26 page)
Presuming it won't, let's look at travel amongst the Jovian System. First, discard the outer satellites: they're retrograde, and take so much delta v to catch that if you can land on them, you can go nearly anywhere. The others are more reasonable, and the delta v's for travel among them are given in Figure 21. Except for Amalthea down there close to Jupiter, we can do it all with NERVA-style ships. Moreover, the travel times are very short, and you get favorable geometry for Hohmann transfer every couple of months or less. The four big Galilean Moons take about as much delta v to travel among as it took to get out there in the first place, but if they're hydrogen-rich, fueling your NERVA will be no problem.
The outer three rocks are very easy to travel among, and you could do it with a backyard rocket burning kerosene. Since those rocks are probably captured asteroids, they're as likely to be interesting as any of the others the Belters are concerned about.
So we can end on a cheerful note, saying Goodbye to the Belters, but also making ready to greet the Minister Plenipotentiary and Ambassador Extraordinary from the Jovian Moons.
__________
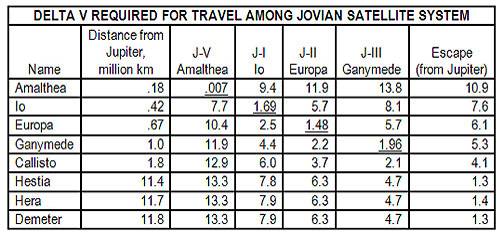
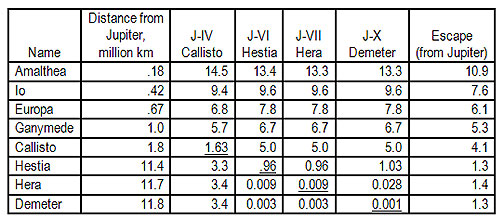
Ships for Manned SpaceflightAll values are in km/sec. Values below the
diagonal
are delta v's needed to go from orbit around one satellite to orbit around the other, landing on neither. Values above the diagonal are surface-to-surface velocity change requirements.
Diagonal
values are the circular orbital velocities of the moons.
Escape is velocity change required to leave the Jupiter system entirely.
I was recently caught in an argument between Rusty Schweikert, astronaut-scientist, and Gene Thorley, Chief of the NASA Earth Resources Survey. After a while I had a sense of
déjà vu:
the man-in-space people have been fighting with the black box boys at least since 1954 when I first got involved in the space business.
The arguments haven't changed, although you'd have thought Skylab might Have ended it; but no, the black box boys still say that anything a man can do in space, instrument probes can do better and cheaper—and two instrument missions cost less than one manned mission. Meanwhile, the astronauts say that you can't learn anything from a probe that you hadn't thought to ask it to tell you, and a trained astronaut-scientist will think of new experiments while he's in space and can do them.
I won't pretend neutrality, having started in the Human Factors laboratories and put several years into work on keeping men alive in the space environment; obviously I'm prejudiced in favor of the astronauts.
Unfortunately, the black box boys have a strong point. It's going to cost a
lot
to send manned missions to the planets, and with present spacecraft, manned interplanetary travel can
never
become routine. It's not just a question of refining what we've got, either; there's a definite theoretical limit to what we can do with chemical rockets, and manned interplanetary cruises—other than spectacular one-shots to say we've done it—are beyond those limits.
Let's see why and then look at ships that
can
take man to the planets.
First we'll need a couple of basic facts about propulsion. Jim Baen and I are agreed that this chapter won't become a substitute for a textbook, and I'll keep the lecture short.
Rockets are still the only means of interplanetary travel we have, and they work by throwing mass overboard. The more mass tossed, and the faster it goes, the more thrust:
Thrust (force) = (rate of mass loss) x (exhaust velocity)
or T = (M
0
-M
1
) x (V
e
) / t (Equation1)
What this says is you take the weight of the ship when you get through burning fuel, subtract that from the weight you started with, divide by time of burn and multiply by the velocity the burned fuel went aftwards from the ship; and you get thrust. Now in the foot/pound measurement system, thrust is expressed in
pounds
and sounds like a weight. It's not, it's a force, but it does have one convenient property.
One pound of thrust will just support one pound of weight in the gravity of the Earth's surface. It will accelerate that same mass at one gravity if you started in orbit. In metric systems, thrust is expressed in newtons or dynes, and if you don't understand the difference between
mass
and
weight,
they aren't easy to interpret However, equation one makes it easy to see that if you don't want to throw much mass overboard, you'd better get it going aft at a fast clip—that is, you need high V
e
.
Now V
e
happens to be related to the temperature of the burn in the rocket engine, so naturally there's a limit to how high that can get; if it's hot enough, the engine melts, and your rocket won't work so good. It should be clear, though, that the theoretical V
e
obtainable with any given combination of fuel and oxidizer is a good measure of how efficient that would be as a rocket fuel.
However, for reasons I won't go into, instead of V
e
most engineers use another measure of fuel efficiency known as Specific Impulse, abbreviated I
sp
; and this is given in units called "seconds." That's not really a unit of time. I
sp
is the "pounds of thrust obtained per pound of fuel expended per second," obviously a measure of efficiency; and
I
sp
=
V
e
/ g (Equation 2)
where g is the acceleration of gravity: 980 cm/sec/sec in the metric system and 32 ft./sec/sec in the English.
Now we have a measure of fuel efficiency, but we don't know
"what
we need for interplanetary travel. As I've shown before in these columns, one of the most convenient figures to look at is "delta vee," meaning the total change in velocity we can get from a ship if we burn all the fuel in it. Delta v is convenient because it doesn't matter if you burn all the fuel at once, or keep turning the motor on and off; and furthermore, we can calculate the delta v needed for various space missions without knowing anything about the ships at all. Big or little, it takes the same delta v to get into orbit, or to go from here to Mars.
We're almost done with the rocketry basics, but we need one more equation:
Delta v =V
e
log
e
(M
0
/M
1
) (Equation 3)
What this says is that the total velocity change you can get from a rocketship can be found by knowing the exhaust velocity of the fuel burned, and the ratio of the mass when you started to the mass when you finished the mission. Log-base-e is the "Natural log" of that ratio, and if you don't understand logs, don't worry about it. It's tabled in handbooks or given by scientific pocket computers.*
Early chemical rockets used fuel/oxidizer combinations with I
sp
of under 200 seconds. That means that at a mass flow rate of 1 pound a second, the rocket could lift about 200 pounds against gravity. Recall, though, that this is the total weight lifted, including the fuel to be burned in the next seconds, etc., and you'll see it's not so good after all.
Incidentally, if you'll look at the three equations you'll see why liquid-fuel rockets start lifting slowly and get faster and faster as they rise. The mass-flow stays the same, but they're burning fuel and getting lighter all the time. Since the thrust hasn't changed, but the mass it has to lift is decreasing, the acceleration the motor can impart to the rocket is increasing all the time.
Rocket chemists worked very hard to get higher I
sp
(and thus higher exhaust velocities), and now the best solid-fuel rockets have I
sp
in the order of 250 seconds. Meanwhile, liquid-fuel rocket motors were developed to give even higher specific impulses, and by using liquid oxygen (LOX) and routing that around the motor to cool it before it was burned, higher burning temperatures were achieved. Eventually, LOX made I
sp
of 300 nearly routine. More exotic fuels were employed, including liquid hydrogen with LOX, and finally hydrogen and fluorine.
___________
* An easier way to calculate delta v is to send $3.00 to RAND CORPORATION, 1700 Main St., Santa Monica, Calif. 90406 and ask for a "Rocket Performance Computer." It's a circular slide rule developed by Ed Sharkey, and it comes with a book of instructions. You enter with I
sp
and mass ratio and it gives delta v directly.
__________
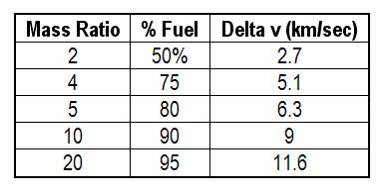
TABLE ONE
Best Delta v for chemical rockets.
I
sp
= 400 V
p
= 3.9 km/sec
__________
However, with the best chemical fuels, the theoretical maximum I
sp
is no more than 400. Actually, no one has got
that yet;
and it's certain that no chemical rocket will do better.
I
sp
of 400 is an exhaust velocity, at best, of 3.9 kilometers/second. Let's plug that into equation three for various mass ratios and see what happens. (Table One.)
It takes about 8 km/second to get into Earth orbit, which means the best chemical rockets have to be almost 90% fuel simply to get to orbit in a single stage; but let's assume we start in Earth orbit.
To get to Mars requires about 5.5 km/sec velocity if you
start
in Earth orbit—and it takes that much again to get back. Clearly, if we're to carry any payloads to Mars, we need refueling out there.
Equally clearly, we've got a problem, because how do we ferry enough equipment to set up a fueling station on Mars? About 80% of our payload put into Earth orbit gets burned before we reach Mars.
To make a round trip, which means carrying the fuel to come home with, we have to put 20 pounds into Earth orbit for each pound making the trip from Earth to Mars and back again. Even one way takes a factor of 4 to 1, not impossible, but expensive enough. Still, we could imagine commerce in which 4 tons of fuel were burned for each ton of payload delivered.
Unfortunately, minimum energy transfers (and those are the only kind possible with chemical rockets; anything else required delta v in the tens to hundreds of km/sec) takes
time:
260 days to Mars.
People eat, drink, and breathe. With the best recycling we're going to have consumables aboard the ships—and the recycling systems are massive, too. Let's be generous and say we hold things to 5 pounds a day per passenger, and start with people who weigh 200 pounds each. That's 1500 pounds of passenger and consumables—and 6000 pounds of fuel for his one-way trip.
If we can't refuel at Mars and have to carry our return LOX and hydrogen out with us, it's far worse. You need 150,000 pounds of fuel in Earth orbit for each round trip passenger. Clearly, that's not a commercial proposition. Chemical rockets can give us commerce with Mars only if we can build a Mars orbiter and fueling station, and even then it's marginal: and remember, we've given chemical rockets the best possible performance. It's not good enough.
What are the alternatives, then? We have several, one of which could have been developed by the end of this decade.