Coming of Age in the Milky Way (15 page)
Read Coming of Age in the Milky Way Online
Authors: Timothy Ferris
Tags: #Science, #Philosophy, #Space and time, #Cosmology, #Science - History, #Astronomy, #Metaphysics, #History
Yet the man whose explication of the cosmos lives on in a billion minds was himself one of the strangest and most remotely inaccessible individuals who ever lived. When John Maynard Keynes purchased a trunk full of Newton’s papers at auction, he was startled to find that it was full of notes on alchemy, biblical prophecy, and the reconstruction from Hebraic texts of the floor plan of the temple of Jerusalem, which Newton took to be “an emblem of the system of the world.” “Newton was not the first of the age of reason,” a shaken Keynes told a gathering at the Royal Society. “He was the last of the magicians, the last of the Babylonians and Sumerians.”
1
Newton was isolated, too, by the singular power of his intellect. Richard Westfall spent twenty years writing a highly perceptive scholarly biography of Newton, yet confessed, in the first paragraph of its preface, that
The more I have studied him, the more Newton has receded from me. It has been my privilege at various times to know a number of brilliant men, men whom I acknowledge without hesitation to be my intellectual superiors. I have never, however, met one against whom I was unwilling to measure myself, so that it seemed reasonable to say that I was half as able as the person in question, or a third or a fourth, but in every case a finite fraction. The end result of my study of Newton has served to convince me that with him there is no measure. He has become for me wholly other, one of the tiny handful of supreme geniuses who have shaped the categories of the human intellect, a man not finally reducible to the criteria by which we comprehend our fellow beings.
2
Newton was an only child, the posthumous son of an illiterate yeoman. Born prematurely—so small, his mother used to say, that he could have fit in a quart bottle—he was not expected to survive. His mother, a widow with a farm to manage, soon remarried, and her new husband, the Reverend Barnabus Smith, sent the child off to be raised by his maternal grandmother; there he grew up, only a mile and a half away, within sight of the house where dwelt his loving mother and usurping stepfather. The product of all this—
a fatherless birth on Christmas Day, survival against the odds, separation from his mother, and possession of a mind so powerful that he was as much its vassal as its master—was a brooding, simmering boy, sullen and bright and quick to anger. At age twenty Newton compiled a list of his youthful sins; among them were “threatening my father and mother Smith to burne them and the house over them,” “peevishness with my mother,” “striking many,” and “wishing death and hoping it to some.”
3
The young Newton was as sensitive to the rhythms of nature as he was indifferent to those of men. As a child he built clocks and sundials and was known for his ability to tell time by the sun, but he habitually forgot to show up for meals, a trait that persisted throughout his life, and he was far too fey to help out reliably on the farm. Sent to gather in livestock, he was found an hour later standing on the bridge leading to the pasture, gazing fixedly into a flowing stream. On another occasion he came home trailing a leader and bridle, not having noticed that the horse he had been leading had slipped away. A sometime practical joker, he alarmed the Lincolnshire populace one summer night by launching a hot-air flying saucer that he constructed by attaching candles to a wooden frame beneath a wax paper canopy.
*
He seldom studied and customarily fell behind at grammar school, but applied himself at the end of each term and surpassed his classmates on final examinations, a habit that did little to enhance his popularity. A contemporary of Newton’s reported that when the boy left for Cambridge, the servants at Woolsthorpe Manor “rejoiced at parting with him, declaring, he was fit for nothing but the ’Versity.”
4
At college he filled his lonely life with books.
“Amicus Plato amicus Aristoteles magis arnica Veritas,’”
he wrote in his student notebook—“Plato is my friend, Aristotle is my friend, but my greatest friend is truth.”
5
He seems to have made the acquaintance of only one of his fellow students, John Wickins, who found him walking in the gardens “solitary and dejected” and took pity on him. Newton’s studies, like those of many a clever undergraduate, were eclectic—he looked into everything from universal languages to perpetual motion machines—but he pursued them with a unique intensity. Nothing, least of all his personal comfort, could deter him when he was on to a question of interest: To investigate the
anatomy of the eye he stuck a bodkin “betwixt my eye and the bone as near to the backside of my eye as I could,” and he once stared at the sun for so long that it took days of recuperation in a dark room before his vision returned to normal.
For a time he drew inspiration from the books of Rene Descartes, a kindred spirit. Descartes like Newton had been a frail child, brought up by his grandmother, and both men were seized by an all-embracing vision while in their early twenties: Newton’s epiphany was universal gravitation; Descartes’s involved nothing less than a science of all human knowledge. Descartes died in 1650, more than a decade before Newton arrived at Cambridge, but his works were very much alive among the “brisk part” of the faculty—those whose intellectual horizons were not bounded by Aristotle’s.
*
But if Newton learned a great deal from Descartes’s
Principia Philosophiae
—which included, among many other things, an assertion that inertia involves resistance to changes in motion and not just to motion itself—he was always happiest in contention, and Descartes’s philosophy promoted in him an equal and opposite reaction. Descartes’s disapproval of atomism helped turn Newton into a confirmed atomist. Descartes’s vortex theory of the solar system became the foil for Newton’s demonstration that vortices could not account for Kepler’s laws of planetary motion. Descartes’s emphasis on depicting motion algebraically encouraged Newton to develop a dynamics written in terms of algebra’s alternative, geometry; as this was not yet mathematically feasible, Newton found it necessary to invent a new branch of mathematics, the calculus. Infinitesimal calculus set geometry in motion: The parabolas and hyperbolas Newton drew on the page could be analyzed as the product of a moving point, like the tip of the stick with which Archimedes drew figures in the sand. As Newton put it, “Lines are described, and thereby generated not by the opposition of parts, but by the continued motion of points.” Here the unbending Newton danced.
Newton had completed this work by the time he received his bachelor’s degree, in April 1665. It would have established him as the greatest mathematician in Europe (and as the most accomplished undergraduate in the history of education) but he published none of it. Publication, he feared, might bring fame, and fame abridge his privacy. As he remarked in a letter written in 1670, “I see not what there is desirable in public esteem, were I able to acquire and maintain it. It would perhaps increase my acquaintance, the thing which I chiefly study to decline.”
6
Soon after his graduation the university was closed owing to an epidemic of the plague, and Newton went home. There he had ample time to think. One day (and it seems quite plausibly to have dawned on him all at once) he hit upon the grand theory that had eluded Kepler and Galileo—a single, comprehensive account of how the force of gravitation dictates the motion of the moon and planets. As he recounted it:
In those days I was in the prime of my age for invention & minded Mathematics & Philosophy more than at any time since. … I began to think of gravity extending to the orb of the Moon & … from Kepler’s rule of the periodical times of the Planets being in sesquialterate proportion of their distances from the center of their Orbs, I deduced that the forces which keep the planets in their Orbs must [be] reciprocally as the squares of their distances from the centers about which they revolve: & thereby compared the force requisite to keep the Moon in her Orb with the force of gravity at the surface of the earth, & found them answer pretty nearly.
7
Newton is said to have recalled, near the end of his life, that this inspiration came to him when he saw an apple fall from the tree in front of his mother’s house. The story may be true—Newton’s desk in his bedroom looked out on an apple orchard, and even a Newton must occasionally have interrupted his work to gaze out the window—and it serves, in any event, to trace how he arrived at a quantitative description of gravitation that drew together the physics of the heavens and the earth.
Suppose, as Newton did that day, that the same gravitational force responsible for the apple’s fall extends “to the orb of the Moon,” and that its force decreases by the square of the distance
over which it propagates.
*
The radius of the earth is 4,000 miles, meaning that Newton and his apple tree were located 4,000 miles from a point at the center of the earth from which (and this was one of Newton’s key insights) the gravitational force of the earth emanates. The moon’s distance from the center of the earth is 240,000 miles—60 times farther than that of the apple tree. If the inverse-square law holds, the falling apple should therefore experience a gravitational force 60
2
, or 3,600, times stronger than does the moon. Newton assumed, from the principle of inertia, that the moon would fly away in a straight line, were it not constantly tugged from that path by the force of the earth’s gravity. He calculated how far the moon “falls” toward the earth—i.e., departs from a straight line in order to trace out its orbit—every second. The answer was 0.0044 feet per second. Multiplying 0.0044 by 3,600 to match the proposed strength of gravitation at the earth’s surface yielded 15.84 feet per second, or “pretty nearly” the 16 feet per second that an apple, or anything else, falls on Earth. This agreement confirmed Newton’s hypothesis that the same gravitational force that pulls the apple down pulls at the moon, too.
Having done the calculation, Newton silently set it aside. Various explanations can be offered for his quietude: The calculations fit “pretty nearly” but not perfectly, owing to inaccuracies in the estimated distance to the moon; Newton was interested in other matters, among them the binomial series and the nature of color; and, in any event, he seldom felt any impulse to call attention to himself: He didn’t publish the calculus, either, for twenty-seven years, and then anonymously.

The young Newton’s realization on universal gravitation went as follows: If the moon is 60 times as far from the center of the earth as is the apple (4,000 miles for the apple, 240,000 miles for the moon), and gravitation diminishes by the square of the distance, then the apple is subject to a gravitational force 60
2
, or 3,600, times that experienced by the moon. The moon, therefore, should “fall” along the curve of its orbit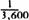 th each second as does the apple. And so it does (time AB = time CD).
th each second as does the apple. And so it does (time AB = time CD).
A few academic colleagues did become acquainted with elements of Newton’s research, however, and two years after returning to Trinity College, Cambridge, he was named Lucasian Professor of Mathematics. (The position had been vacated by his favorite teacher, the blustery and witty mathematician Isaac Barrow, who left to take up divinity studies and died seven years later of an opium overdose.) But Newton the teacher had little more in common with his colleagues than had Newton the student. Numerous among the professors were the so-called “wet epicures,” their lives spent, wrote the satirist Nicholas Amherst, “in a supine and regular course of eating, drinking, sleeping, and cheating the juniors.”
8
Others were known as much for their eccentricities as for their scholarship; the master of Trinity, for one, was an effeminate shut-in who kept enormous house spiders in his rooms as pets. Not that Newton had any difficulty holding his own when it came to idiosyncrasies. Gaunt and disheveled, his wig askew, he dressed in run-down shoes and soiled linen, seldom stopped working, and frequently forgot to sleep. Once, puzzling over why he seemed to be losing his mental agility while working on a problem, he reflected on the matter, realized that he had not slept for days, and reluctantly went to bed. He forgot to eat as well, often rising from his desk at dawn to breakfast on the congealed remains of the dinner that had been brought to him and left untouched the night before. His rare efforts at conviviality fared poorly; one night while entertaining a few acquaintances he went to his room to fetch a bottle of wine, failed to return, and was found at his desk, hunched over his papers, wine and guests forgotten.