Coming of Age in the Milky Way (29 page)
Read Coming of Age in the Milky Way Online
Authors: Timothy Ferris
Tags: #Science, #Philosophy, #Space and time, #Cosmology, #Science - History, #Astronomy, #Metaphysics, #History
The same ambiguity applies in the opposite situation: Suppose that when you awaken you find yourself standing in the elevator
car, at your normal weight. This time the instructions say that you are either (1) aboard a elevator stopped on the ground floor of an office building on Earth, or (2) adrift in zero-gravity space, in an elevator attached by a cable to a spaceship that is pulling it away at a steady acceleration, pressing you to the floor with a force equal to that of Earth’s gravitation—at one “G,” as the jet pilots say. Here again, you cannot prove which is the case.
Einstein reasoned that if the effects of gravitation are mimicked by acceleration, gravitation itself might be regarded as a kind of acceleration. But acceleration through what reference frame? It could not be ordinary three-dimensional space; the passengers in the elevator in the New York skyscraper, after all, are not flying through space relative to the earth.
The search for an answer required brought Einstein to consider the concept of a four-dimensional spacetime continuum. Within its framework, gravitation
ts
acceleration, the acceleration of objects as they glide along “world lines”—paths of least action traced over the slopes of a three-dimensional space that is curved in the fourth dimension.
A forerunner here was Hermann Minkowski, who had been Einstein’s mathematics professor at the Polytechnic Institute. Minkowski remembered Einstein as a “lazy dog” who seldom came to class, but he was quick to appreciate the importance of Einstein’s work, though initially he viewed it as but an improvement on Lorentz. In 1908 Minkowski published a paper on Lorentz’s theory that cleared away much of the mathematical deadwood that had cluttered Einstein’s original formulation of special relativity. It demonstrated that time could be treated as a dimension in a four-dimensional universe. “Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality,” Minkowski predicted.
34
His words proved prophetic, and the special theory of relativity has been viewed in terms of a “spacetime continuum” ever since. Einstein initially dismissed Minkowski’s formulation as excessively pedantic, joking that he scarcely recognized his own theory once the mathematicians got hold of it. But he came to realize that if he were to explore the connection between weight and inertia, he would do well to travel farther up the trail Minkowski had blazed.
Minkowski’s spacetime continuum, though suitable for special
relativity, would not support what was to become general relativity. Its space was “flat”—i.e., euclidean. If gravitation were to be interpreted as a form of acceleration, that acceleration would have to occur along the undulations of curved space. So it was that Einstein was led, however reluctantly, into the forbidding territory of the noneuclidean geometries.
Euclidean geometry, as every high school math student is taught, has different characteristics depending upon whether it is worked in two dimensions (“plane” geometry) or three (“solid” geometry). On a plane, the sum of the angles of a triangle is 180 degrees, but if we add a third dimension we can envision surfaces such as that
of a sphere, on which the angles of a triangle add up to
more
than 180 degrees, or a saddle-shaped hyperbola, on which the angles add up to
less
than 180 degrees. The shortest distance between two points on a plane is a straight line, but on a sphere or a hyperbola the shortest distances are
curved
lines. In the noneuclidean geometries a fourth dimension is added, and the rules are changed in a similarly consistent manner to allow for the possible curvature of three-dimensional space within a four-dimensional theater. Two categories of curved space then can be imagined (or at least calculated): spherical, or “closed” space, in which three-space obeys geometrical rules analogous to those of the two-space on the surface of a sphere, and hyperbolic, or “open” space, analogous to the surface of a three-dimensional hyperbola. (One can also work out a flat, euclidean four-dimensional geometry, but in that case the rules do not change, just as plane two-dimensional geometry obeys the same rules if the planes happen to be the sides of a three-dimensional cube.)

Triangles in flat two-dimensional space have interior angles that always add up to 180 degrees. But when two-space is curved into a third dimension, the angles always total either
less
than 180 degrees (if the curvature is hyperbolic, or “open”) or
more
than 180 degrees (if the curvature is spherical, or “closed”). Similarly, the geometry of the three-dimensional universe may be either flat (euclidean), or open or closed (noneuclidean), when viewed in the context of Einstein’s four-dimensional spacetime continuum.
By the time Einstein came on the scene, the rules of four-dimensional geometry had been worked out—those of spherical four-space by Georg Friedrich Riemann and those of the four-dimensional hyperbolas by Nikolai Ivanovich Lobachevski and János Bolyai. The whole subject, however, was still regarded as at best difficult and arcane, and at worst almost disreputable.
*
The legendary mathematician Karl Friedrich Gauss had withheld his papers on noneuclidean geometry from publication, fearing ridicule by his colleagues, and Bolyai conducted his research in the field against the advice of his father, who warned him, “For God’s sake, please give it up. Fear it no less than the sensual passions because it, too, may take up all your time and deprive you of your health, peace of mind and happiness in life.”
36
Einstein rushed in where Bolyai’s father feared to tread. With the aid of his old classmate Marcel Grossmann—“Help me, Marcel,
or I’ll go crazy!” he wrote—Einstein struggled through the complexities of curved space, seeking to assign the fourth dimension to time and make the whole, infernally complicated affair come out right. He had by now begun to win professional recognition, had quit the patent office to accept a series of teaching positions that culminated in a full professorship in pure research at the University of Berlin, and was doing important work in quantum mechanics and a half-dozen other fields. But he kept returning to the riddle of gravitation, trying to find patterns of beauty and simplicity among thick stacks of papers black with equations. Like a lost explorer discarding his belongings on a trek across the desert, he found it necessary to part company with some of the most cherished of his possessions—among them one of the central precepts of the special theory itself, which to his joy was ultimately to return as a local case within the broader scheme of the general theory. “In all my life I have never before labored so hard,” he wrote to a friend. “… Compared with this problem, the original theory of relativity is child’s play.”
37
Nowhere in human history is there to be found a more sustained and heroic labor of the intellect than in Einstein’s trek toward general relativity, nor one that has produced a greater reward.
He completed the theory in November 1915 and published it the following spring. Though its equations are complex, its central conception is startlingly simple. The force of gravitation disappears, and is replaced by the geometry of space itself: Matter curves space, and what we call gravitation is but the acceleration of objects as they slide down the toboggan runs described by their trajectories in time through the undulations of space. The planets skid along the inner walls of a depression in space created by the fat, massive sun; clusters of galaxies rest in spatial hollows like nuggets in a prospector’s bowl.
In marrying gravitational physics to the geometry of curved space, general relativity emancipated cosmology from the ancient dilemma of whether the universe is infinite and unbounded or finite and bounded. An infinite universe would be not just large but
infinite
, and this posed problems. The gravitational force generated by an infinite number of stars would itself be infinite, and would, therefore, overwhelm the local action of gravity; this prospect so troubled Newton that he resorted to invoking God’s infinite grace to resolve it. Moreover, the light from an infinite number of stars
might be expected to turn the night sky into a blazing sheet of light; yet the night sky is dark.
*
The alternative, however—a finite euclidean universe with an edge to it—was equally unattractive: As Liu Chi posed the question, in China in the fourteenth century, “If heaven has a boundary, what things could be outside it?”
39
The difficulty of imagining an end to space had been enunciated as early as the fifth century
B.C.
, by Plato’s colleague Archytas the Pythagorean; Lucretius summed it up this way:
Let us assume for the moment that the universe is limited. If a man advances so that he is at the very edge of the extreme boundary and hurls a swift spear, do you prefer that this spear, hurled with great force, go where it was sent and fly far, or do you think that something can stop it and stand in its way?
40
General relativity resolved the matter by establishing that the universe could be both finite—i.e., could contain a finite number of stars in a finite volume of space—and unbounded. The key to this realization lay in Einstein’s demonstration that, since matter warps space, the sum total of the mass in all the galaxies might be sufficient to wrap space around themselves. The result would be a closed, four-dimensionally spherical cosmos, in which any observer, anywhere in the universe, would see galaxies stretching deep into space in every direction, and would conclude, correctly, that there is no end to space. Yet the amount of space in a closed universe would nonetheless be finite: An adventurer with time to spare could eventually visit every galaxy, yet would never reach an edge of space. Just as the surface of the earth is finite but unbounded in two dimensions (we can wander wherever we like, and will not fall off the edge of the earth) so a closed four-dimensional universe is finite but unbounded to us who observe it in three dimensions.
†
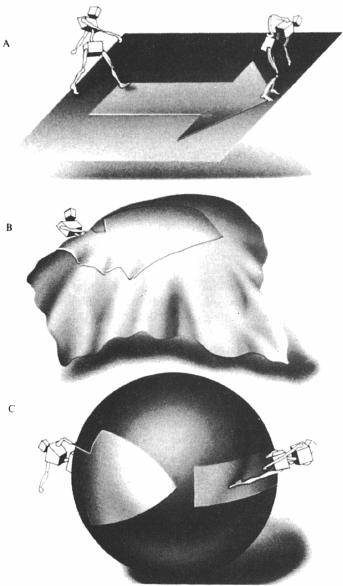
Two-dimensional inhabitants of a finite universe must confront the paradox of an “edge” to their cosmos. But if we add a dimension, curving the plane on which they live into a sphere, their world, though still finite, becomes unbounded. General relativity reveals a similar prospect for the four-dimensional geometry of the universe we three-dimensional creatures inhabit: hence Einstein’s “closed, unbounded” universe.
The question of whether the universe is hyperbolic and open or spherical and closed remains unanswered, as we shall see. But, thanks to Einstein, the problem is no longer clouded by paradox. By introducing the scientific prospect of a finite, unbounded cosmos, Einstein’s general theory initiated a meaningful dialogue between the human mind and the conundrums of cosmological space.
The theory was beautiful, but was it true? Einstein, having been to the mountaintop, felt supremely confident on this score. General relativity explained a precession in the orbit of the planet Mercury that had been left unaccounted for in Newtonian mechanics, and he did not doubt it would survive further tests as well. As he wrote his friend Besso, “I am fully satisfied, and I do not doubt any more the correctness of the whole system…. The sense of the thing is too evident.”
41
The wider scientific community, however, awaited the verdict of experiment. There would be a total solar eclipse on May 29, 1919, at which time the sun would stand against the bright stars of the Hyades cluster. The English astronomer Arthur Stanley Eddington led an expedition to a cocoa plantation on Principe Island off west Equatorial Africa to observe the eclipse and see whether the predicted curvature of space in the region of the sun would distort the apparent positions of the stars in the briefly darkened sky. It was a scene of high drama—English scientists testing the theory of a German physicist immediately after the end of the Great War. As the time of the eclipse approached, rain clouds covered the sky. But then, moments after the moon’s shadow came speeding across the landscape and totality began, a hole opened up in the clouds around the sun, and the camera shutters were triggered. The results of Eddington’s expedition, and of a second eclipse observation conducted at Sobral, Brazil on the same day, were presented by the Astronomer Royal at a meeting of the Royal Society in London on November 6, 1919, with Newton’s portrait looking on. They were positive: The light rays coming from the stars of the Hyades were found to be offset to just the degree predicted in the theory.