Data Mining (110 page)
Authors: Mehmed Kantardzic
9.
Review the latest articles on privacy-preserving data mining that are available on the Internet. Discuss the trends in the field.
10.
What are the largest sources of unintended personal data on the Internet? How do we increase awareness of Web users of their personal data that are available on the Web for a variety of data-mining activities?
11.
Discuss an implementation of transparency and accountability mechanisms in a data-mining process. Illustrate your ideas with examples of real-world data-mining applications.
12.
Give examples of data-mining applications where you would use DDM approach. Explain the reasons.
12.8 REFERENCES FOR FURTHER STUDY
Aggarwal C. C., P. S. Yu,
Privacy-Preserving Data Mining: Models and Algorithms
, Springer, Boston, 2008.
The book proposes a number of techniques to perform the data-mining tasks in a privacy-preserving way. These techniques generally fall into the following categories: data modification techniques, cryptographic methods and protocols for data sharing, statistical techniques for disclosure and inference control, query auditing methods, and randomization and perturbation-based techniques. This edited volume contains surveys by distinguished researchers in the privacy field. Each survey includes the key research content as well as future research directions.
Privacy-Preserving Data Mining: Models and Algorithms
is designed for researchers, professors, and advanced-level students in computer science, and is also suitable for industry practitioners.
Chakrabarti D., C. Faloutsos, Graph Mining: Laws, Generators, and Algorithms,
ACM Computing Surveys
, Vol. 38, March 2006, pp. 1–69.
How does the Web look? How could we tell an abnormal social network from a normal one? These and similar questions are important in many fields where the data can intuitively be cast as a graph; examples range from computer networks to sociology to biology and many more. Indeed, any
M
:
N
relation in database terminology can be represented as a graph. A lot of these questions boil down to the following: “How can we generate synthetic but realistic graphs?” To answer this, we must first understand what patterns are common in real-world graphs and can thus be considered a mark of normality/realism. This survey gives an overview of the incredible variety of work that has been done on these problems. One of our main contributions is the integration of points of view from physics, mathematics, sociology, and computer science. Further, we briefly describe recent advances on some related and interesting graph problems.
Da Silva J. C., et al., Distributed Data Mining and Agents,
Engineering Applications of Artificial Intelligence
, Vol. 18, No. 7, October 2005, pp. 791–807.
Multi-Agent Systems (MAS) offer an architecture for distributed problem solving. DDM algorithms focus on one class of such distributed problem solving tasks—analysis and modeling of distributed data. This paper offers a perspective on DDM algorithms in the context of multi-agent systems. It discusses broadly the connection between DDM and MAS. It provides a high-level survey of DDM, then focuses on distributed clustering algorithms and some potential applications in multi-agent-based problem-solving scenarios. It reviews algorithms for distributed clustering, including privacy-preserving ones. It describes challenges for clustering in sensor-network environments, potential shortcomings of the current algorithms, and future work accordingly. It also discusses confidentiality (privacy preservation) and presents a new algorithm for privacy-preserving density-based clustering.
Laxman S., P. S. Sastry, A Survey of Temporal Data Mining,
Sadhana
, Vol. 31, Part 2, April 2006, pp. 173–198.
Data mining is concerned with analyzing large volumes of (often unstructured) data to automatically discover interesting regularities or relationships that in turn lead to better understanding of the underlying processes. The field of temporal data mining is concerned with such analysis in the case of ordered data streams with temporal interdependencies. Over the last decade many interesting techniques of temporal data mining were proposed and shown to be useful in many applications. Since temporal data mining brings together techniques from different fields such as statistics, machine learning, and databases, the literature is scattered among many different sources. In this article, we present an overview of the techniques of temporal data mining.We mainly concentrate on algorithms for pattern discovery in sequential data streams. We also describe some recent results regarding statistical analysis of pattern discovery methods.
Mitsa T.,
Temporal Data Mining
, Chapmann & Hall/CRC Press, Boca Raton, FL, 2010.
From basic data-mining concepts to state-of-the-art advances,
Temporal Data Mining
covers the theory of this subject as well as its application in a variety of fields. It discusses the incorporation of temporality in databases as well as temporal data representation, similarity computation, data classification, clustering, pattern discovery, and prediction. The book also explores the use of temporal data mining in medicine and biomedical informatics, business and industrial applications, Web-usage mining, and spatiotemporal data mining. Along with various state-of-the-art algorithms, each chapter includes detailed references and short descriptions of relevant algorithms and techniques described in other references. In the appendices, the author explains how data mining fits the overall goal of an organization and how these data can be interpreted for the purposes of characterizing a population. She also provides programs written in the Java language that implement some of the algorithms presented in the first chapter.
Pearl, J.,
Causality: Models, Reasoning and Inference
, 2nd edition, Cambridge University Press, Cambridge, UK, 2009.
This book fulfills a long-standing need for a rigorous yet accessible treatise on the mathematics of causal inference. Judea Pearl has done a masterful job of describing the most important approaches and displaying their underlying logical unity. The book deserves to be read by all scientists who use nonexperimental data to study causation, and would serve well as a graduate or advanced undergraduate course text. The book should prove invaluable to researchers in AI, statistics, economics, epidemiology, and philosophy, and, indeed, all those interested in the fundamental notion of causality. It may well prove to be one of the most influential books of the next decade.
Zeitouni K., A Survey of Spatial Data Mining Methods: Databases and Statistics Point of View, in
Data Warehousing and Web Engineering
, S. Becker, ed., IRM Press, Hershey, PA, 2002.
This chapter reviews the data-mining methods that are combined with GIS for carrying out spatial analysis of geographic data. We will first look at data-mining functions as applied to such data and then highlight their specificity compared with their application to classical data. We will go on to describe the research that is currently going on in this area, pointing out that there are two approaches: The first comes from learning on spatial databases, while the second is based on spatial statistics. We will conclude by discussing the main differences between these two approaches and the elements they have in common.
13
GENETIC ALGORITHMS
Chapter Objectives
- Identify effective algorithms for approximate solutions of optimization problems described with large data sets.
- Compare basic principles and concepts of natural evolution and simulated evolution expressed through genetic algorithms (GAs).
- Describe the main steps of a genetic algorithm with illustrative examples.
- Explain standard and nonstandard genetic operators such as a mechanism for improving solutions.
- Discuss a schema concept with “don’t care” values and its application to approximate optimization.
- Apply a GA to the traveling-salesman problem (TSP) and optimization of classification rules as examples of hard optimizations.
There is a large class of interesting problems for which no reasonably fast algorithms have been developed. Many of these problems are optimization problems that arise frequently in applications. The fundamental approach to optimization is to formulate a single standard of measurement—a cost function—that summarizes the performance or value of a decision and iteratively improves this performance by selecting from among the available alternatives. Most classical methods of optimization generate a deterministic sequence of trial solutions based on the gradient or higher order statistics of the cost function. In general, any abstract task to be accomplished can be thought of as solving a problem, which can be perceived as a search through a space of potential solutions. Since we are looking for “the best” solution, we can view this task as an optimization process. For small data spaces, classical, exhaustive search methods usually suffice; for large spaces, special techniques must be employed. Under regular conditions, the techniques can be shown to generate sequences that asymptotically converge to optimal solutions, and in certain cases they converge exponentially fast. But the methods often fail to perform adequately when random perturbations are imposed on the function that is optimized. Further, locally optimal solutions often prove insufficient in real-world situations. Despite such problems, which we call
hard-optimization problems
, it is often possible to find an effective algorithm whose solution is approximately optimal. One of the approaches is based on GAs, which are developed on the principles of natural evolution.
Natural evolution is a population-based optimization process. Simulating this process on a computer results in stochastic-optimization techniques that can often outperform classical methods of optimization when applied to difficult, real-world problems. The problems that the biological species have solved are typified by chaos, chance, temporality, and nonlinear interactivity. These are the characteristics of the problems that have proved to be especially intractable to classical methods of optimization. Therefore, the main avenue of research in simulated evolution is a GA, which is a new, iterative, optimization method that emphasizes some facets of natural evolution. GAs approximate an optimal solution to the problem at hand; they are by nature stochastic algorithms whose search methods model natural phenomena such as genetic inheritance and the Darwinian strife for survival.
13.1 FUNDAMENTALS OF GAs
GAs are derivative-free, stochastic-optimization methods based loosely on the concepts of natural selection and evolutionary processes. They were first proposed and investigated by John Holland at the University of Michigan in 1975. The basic idea of GAs was revealed by a number of biologists when they used computers to perform simulations of natural genetic systems. In these systems, one or more chromosomes combine to form the total genetic prescription for the construction and operation of some organisms. The chromosomes are composed of genes, which may take a number of values called allele values. The position of a gene (its locus) is identified separately from the gene’s function. Thus, we can talk of a particular gene, for example, an animal’s eye-color gene, with its locus at position 10 and its allele value as blue eyes.
Before going into details of the applications of GAs in the following sections, let us understand their basic principles and components. GAs encode each point in a parameter or solution space into a binary-bit string called a chromosome. These points in an n-dimensional space do not represent samples in the terms that we defined them at the beginning of this book. While samples in other data-mining methodologies are data sets given in advance for training and testing, sets of n-dimensional points in GAs are a part of a GA, and they are produced iteratively in the optimization process. Each point or binary string represents a potential solution to the problem that is to be solved. In GAs, the decision variables of an optimization problem are coded by a structure of one or more strings, which are analogous to chromosomes in natural genetic systems. The coding strings are composed of features that are analogous to genes. Features are located in different positions in the string, where each feature has its own position (locus) and a definite allele value, which complies with the proposed coding method. The string structures in the chromosomes go through different operations similar to the natural-evolution process to produce better alternative solutions. The quality of new chromosomes is estimated based on the “fitness” value, which can be considered as the objective function for the optimization problem. The basic relations between concepts in natural evolution and GAs are given in Table
13.1
. Instead of single a point, GAs usually keep a set of points as a population, which is then evolved repeatedly toward a better overall fitness value. In each generation, the GA constructs a new population using genetic operators such as crossover and mutation. Members with higher fitness values are more likely to survive and participate in mating or
crossover operations
.
TABLE 13.1.
Basic Concepts in Genetic Algorithms
| Concept in Natural Evolution | Concept in Genetic Algorithms |
| Chromosome | String |
| Gene | Features in the string |
| Locus | Position in the string |
| Allele | Position value (usually 0 or 1) |
| Genotype | String structure |
| Phenotype | Set of characteristics (features) |
As a general-purpose optimization tool, GAs are moving out of academia and finding significant applications in many other venues. Typical situations where GAs are particularly useful are in difficult optimization cases for which analytical methods do not work well. GAs have been quite successfully applied to optimization problems like wire routing, scheduling, adaptive control, game playing, transportation problems, TSPs, database query optimization, and machine learning. In the last decades, the significance of optimization has grown even further because many important large-scale, combinatorial-optimization problems and highly constrained engineering problems can only be solved approximately. GAs aim at such complex problems. They belong to the class of probabilistic algorithms, yet they are very different from random algorithms as they combine elements of directed and stochastic search. Another important property of genetic-based search methods is that they maintain a population of potential solutions while all other methods process a single point of the search space. Because of these characteristics, GAs are more robust than existing directed-search methods.
GAs are popular because they do not depend on functional derivatives, and they have the following characteristics:
1.
GAs are parallel-search procedures that can be implemented on parallel-processing machines to massively speed up their operations.
2.
GAs are applicable to both continuous- and discrete-optimization problems.
3.
GAs are stochastic and less likely to get trapped in local minima, which inevitably are present in any practical optimization application.
4.
GAs’ flexibility facilitates both structure and parameter identification in complex models.
The GA theory provides some explanations of why, for a given problem formulation, we may obtain convergence to the sought optimal point. Unfortunately, practical applications do not always follow the theory, the main reasons being:
1.
the coding of the problem often moves the GA to operate in a different space than that of the problem itself;
2.
there are practical limits on the hypothetically unlimited number of iterations (generations in the GA); and
3.
there is a limit on the hypothetically unlimited population size.
One of the implications of these observations is the inability of GAs, under certain conditions, to find the optimal solution or even an approximation to the optimal solution; such failures are usually caused by premature convergence to a local optimum. Do not forget that this problem is common not only for the other optimization algorithms but also for the other data-mining techniques.
13.2 OPTIMIZATION USING GAs
Let us note first that without any loss of generality we can assume that all optimization problems can be analyzed as maximization problems only. If the optimization problem is to minimize a function f(x), this is equivalent to maximizing a function g(x) = −f(x). Moreover, we may assume that the objective function f(x) takes positive values in its domain. Otherwise, we can translate the function for some positive constant C so that it will be always positive, that is,
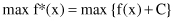
If each variable x
i
, with real values, is coded as a binary string of length
m
, then the relation between the initial value and the coded information is
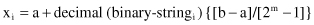
where the variable x
i
can take the values from a domain D
i
= [a, b], and m is the smallest integer such that the binary code has the required precision. For example, the value for variable x given on the domain [10, 20] is a binary-coded string with the length equal to 3 and the code 100. While the range of codes is between 000 and 111, the question is: What is the real value of the coded variable x? For this example, m = 3 and the corresponding precision is
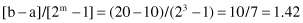
and that is the difference between two successive x
i
values that could be tested as candidates for extreme. Finally, the attribute with the code 100 has a decimal value
