Harnessed: How Language and Music Mimicked Nature and Transformed Ape to Man (27 page)
Read Harnessed: How Language and Music Mimicked Nature and Transformed Ape to Man Online
Authors: Mark Changizi
Tags: #Non-Fiction
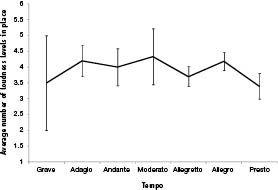
Figure 48
. “Loudness-tessitura” width (i.e., the total range of loudness levels) versus tempo, sampled from 55 pieces in Denes Agay’s
An Anthology of Piano Music, Vol. II: The Classical Period
(used instead of the
Dictionary of Musical Themes
because the latter does not possess loudness information). Unlike (pitch) tessitura width, which is expected—and does—increase with increasing tempo, the loudness-tessitura is expected—and does—remain constant. This anthology was chosen because it was the only proper non-fake, non-lesson book I possessed at home.
We see, then, that faster-tempo music behaves like faster-tempo movers: in each case the range of pitches increases with tempo, and the range of loudnesses does not change. Essentially, these results show us that the physics of movers is found in the structure of music. The upcoming Encore section continues the search for physics in music, and concerns momentum and Newton’s First Law.
7
Newton’s First Law of Music
Objects at rest stay at rest unless pushed. And objects moving continue moving in the same direction unless pushed. This is Newton’s First Law of Motion, which concerns inertia. This is a fundamental law of physics, and applies to any object with mass. Humans have mass, so it applies to us as well. And if music sounds like hulking humans moving about, then even music should adhere to Newton’s First Law of Motion. Does it?
Before attempting to answer this, let’s make sure we steer clear of one of the psychological handicaps I talked about in Chapter 4: the tendency to interpret musical pitch as spatial. As musical notes rise and fall on the page, or as your hands move hither and thither on the piano, it’s hard to resist the feeling that inertia should show up in the musical domain as a tendency for a moving pitch to keep on moving in the same direction. But this is a pitfall. Recall that I am claiming that pitch is about the
direction
of the mover, not about position in space. Changes in pitch are therefore about changes in the mover’s direction, not about changes of position in space.
With our memory jogged about the meaning of pitch, what are the expected musical consequences of Newton’s First Law? A change in melody’s pitch means the fictional mover’s direction of motion has changed. Let’s ask ourselves, then: if a mover changes direction, is there any physical tendency for the mover to
continue
changing direction? Purely physically, Newton’s First Law tells us
no
. Any subsequent turn would require yet more force, without which the mover will continue going in whatever direction it
was
going. When a moving object for some reason makes a 30-degree change in direction, the inertial tendency is precisely
not
to continue turning, but to continue going straight in the new direction. (The same is true if a change in Doppler pitch is due to a change in speed—a change in speed does not lead to a further change in speed—but I’ll always presume movers are staying at constant speed, the relevant case for music at constant tempo.)
The pitch of a mover, then, following the physics of movement itself, tends to stay the same. And if the pitch
does
change, it will have a tendency to stay at the
new
pitch—the mover’s new direction—
not
to continue changing pitch. Newton’s First Law for the pitches of movers is, therefore, that pitches have
no
inertia. Inertia is about how spatial changes tend to continue,
not
about how velocity (speed and direction) changes tend to continue. And because pitch is about velocity (i.e., speed and direction), not spatial location, pitch changes do not tend to continue. (If one
were
to imagine a spatial metaphor for how pitch changes, it would be movement of a bead in thick syrup: it moves if pushed with a fork, but
immediately
halts when no longer pushed.)
If melody’s pitch contour acts like the Doppler pitches of a mover, then musical pitch is expected to have
no
“inertia” to continue moving
in the same direction
—“up” or “down.” I had Sean Barnett carry out an analysis on the entire data set of 10,000 classical themes, and we found that indeed, there was little or no inertia for pitch, just as is expected if melodic pitch contours sound like Doppler pitches from moving humans. In particular, for a one-semitone change, the probability of continuing up after a semitone up was 49.14 percent, and the probability of continuing down after a semitone down was 51.33 percent. For two semitones, the values were 47.06 percent and 56.17 percent. Pitches therefore do not act like spatial location: if pitch were spatial, then a change in pitch
would
tend to lead to more of the same kind of change due to inertia, and those percentages I just mentioned should have all been much greater than 50 percent. Instead, and as predicted, pitches have little or no tendency to continue changing the same way they have been. Pitches act like Doppler shifts, following the expectations of Newton’s First Law of Motion by
not
exhibiting pitch inertia (because inertia does not apply to directions of motion).
Although our data showed no strong bias toward pitch changes continuing in the same direction (which is the signature of true spatial momentum), note that there was, for both one- and two-semitone changes, a
slightly
greater tendency for pitches to go down—a small degree of downward momentum. To further examine this, I need to discuss some subtleties I have glossed over so far.
The ecological interpretation of pitch is the mover’s direction of motion, but more carefully expressed, it is the mover’s direction of motion
relative to the listener
. With this in mind, there are actually
two
fundamentally different ways for a mover’s Doppler pitch to change. The first is what I have assumed in this section thus far: the mover turns. But Doppler pitch
can
change even when the mover does not turn, and this second source of changing Doppler pitch you are very familiar with, because it happens every time a mover passes you, including the generic passing train. When movers pass listeners, their pitch falls. In fact, whenever an object simply moves
straight
its pitch falls (unless the object is directed
perfectly
toward or away from the listener). It is not, then, quite right to say that Doppler pitches have no pitch momentum. Straight-moving movers have falling pitch, and straight-moving movers tend to keep going straight (because of inertia), and therefore falling pitch in
these
circumstances
does
tend to keep on falling.
If only we could tell the difference between the pitch changes due to a mover actually turning and the pitch changes due to a mover simply going straight! We could then predict a lack of pitch momentum for the former, but predict the presence of pitch momentum for the latter. Actually, we
can
tell them apart. When a mover turns, it is intentional and occurs fairly quickly (on average about 45 degrees per step, as discussed earlier in the section of Chapter 4 called “Human Curves”), and it can be a change in direction either more or less toward the listener. Intentional turning behavior therefore tends to lead to large pitch changes that can be upward or downward. But the second source of Doppler pitch change is the one due to movers going straight (and going by). In this case there tend to be a lot of steps over which pitch falls—because now the falling pitch is, in essence, due to continuous change of position in space—and so the pitch change per step is small, and is always downward.
Here, then, is how we can distinguish the straight-moving mover from the turning mover. When pitch falls by only a small amount, it tends to be the signature of a straight-moving mover passing. But when the pitch change is
not
consistently small and downward, it is typically due to the mover turning. Thus, a turning mover is given away by either of two pitch cues: (i) a large pitch change, whether upward or downward, implicates a turning mover, and (ii) any pitch change upward at all, small or large, implicates a turning mover (because straight-moving movers only have falling pitch, not rising pitch).
We do therefore expect Doppler pitch to possess inertia in just one circumstance: when pitch falls by a small amount. Small drops in pitch are more probably attributable to a straight-moving mover. Because straight movers have inertia and are thus likely to continue moving straight, small pitch drops
do
tend to have inertia. Small pitch upswings do not, however, have inertia, and neither do large pitch changes, whether up or down.
Is this what we find in music?
We already saw evidence for this earlier in this section. Recall that there was generally little or no inertia for pitch—the probability of a pitch change continuing in the same direction was near 50 percent. But let’s look at the pitch momentum numbers again, more carefully this time. For a semitone pitch change, the probability of continuing in the same direction was 49.14 percent and 51.33 percent for upward and downward, respectively. (Their standard errors are small—0.005 and 0.004, respectively—because these are averages across many thousands of instances.) The same asymmetry was found when considering whole-step changes of pitch, but now with respective values of 47.06 percent and 56.17 percent. (Standard errors are each 0.004.) These results are consistent with those of Paul von Hippel that David Huron discusses in his book
Sweet Anticipation
: no momentum following small steps upwards, but significant momentum downwards. The signature of pitch momentum is a value greater than 50 percent, and only the downward pitch change has this. (Upward pitch change is below 50 percent, meaning that a little more than half of the time a semitone upward is followed by either no change in pitch or a downward change in pitch.) For larger pitch changes, we found that neither upward nor downward pitch changes had any pitch momentum (i.e., the probability of continuing to change in the same direction was below 50 percent). Not only, then, does melodic pitch contour have a counterintuitive tendency to have no inertia, like the pitches of movers—but it breaks this tendency exactly when movers do. Consistent with melody’s meaning coming from the Doppler shifts of movers, melody conforms to Newton’s law of inertia.
In addition to the issue of whether pitch changes continue to change in the same direction, we can make a simpler observation. Let’s ask ourselves what the baseline expectation is for the Doppler pitch change of a mover. One’s first intuition might be that, in the absence of any information otherwise, we should expect a mover’s Doppler pitch to remain unchanged from one step to the next. Doppler pitches, however, do not typically hold still. Instead, the most fundamental baseline expectation (inertia) is that movers continue moving in whatever direction they
were
going. People tend (though not as strongly as inanimate objects!) to keep going straight, and thus the baseline, or generic expectation, for pitch change is that pitch
falls
, and generally by a small amount (compared to the pitch changes of a turner).
Now consider another observation about movers. Suppose that a mover is carrying out bouts of behavior around you,
and
is directing those behaviors toward you. Notice that this mover will have to make intentional turns toward you to keep orienting his behavior toward you. But also notice that he or she never has to deliberately turn
away
from you. This is because once a mover is directed roughly but not exactly toward you, going straight inevitably leads to a movement like veering away. Simply going straight will cause the mover to pass by you and depart. Turning is necessary to go toward someone, but not to go away. (This is essentially because a listener is in one location, and all the other locations are where that listener is
not
.) Thus, if musical melody is about listener-directed bouts of behavior, not only do we expect small pitch changes to more commonly be downward, we expect large pitch changes to more commonly be upward.
Do we find this in music? Do we find that melodic contours have a general tendency to fall gradually? And do we find that pitch drops tend to be smaller than pitch rises? Piet G. Vos and Jim M. Troost of the University of Nijmegen indeed found this among a sample from the
Dictionary of Musical
Themes
. We carried out our own measurements over the entire data set: Sean Barnett measured the relative probability that a pitch changes upward (so that a probability greater than 0.5 means an upward tendency, and a probability less than 0.5 means a downward tendency) as a function of the size of the pitch change. One can see these results in Figure 49. For small pitch changes, the probabilities are mostly below 0.5, meaning that small pitch changes tend to be downward, as expected. And for large pitch changes the probabilities are mostly above 0.5, meaning that large pitch changes tend to be upward, also as expected.
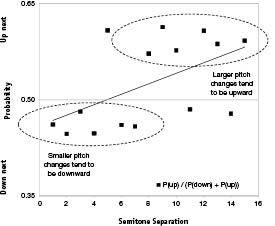
Figure 49
. The y-axis shows the relative probability that a pitch will go up on the next note, among the 10,000 classical themes in Barlow and Morgenstern’s Dictionary. A value of 0.5 means it is equally likely to go up or down in pitch. The x-axis represents how far the pitch changes (in number of semitones). One can see that for small pitch changes the probability tends to be below 0.5, meaning pitches tend to fall. But for large pitch changes, they tend to rise. Sean Barnett, then a graduate student at RPI, made these measurements.