How to Read a Paper: The Basics of Evidence-Based Medicine (14 page)

References

1
Mitchell J. “But will it help
my
patients with myocardial infarction?” The implications of recent trials for everyday country folk
British Medical Journal (Clinical Research Edition)
1982;
285
(6349):1140.

2
McCormack J, Greenhalgh T. Seeing what you want to see in randomised controlled trials: versions and perversions of UKPDS data. United Kingdom prospective diabetes study.
BMJ: British Medical Journal
2000;
320
(7251):1720–3.

3
Phillips AN, Smith GD, Johnson MA. Will we ever know when to treat HIV infection?
BMJ: British Medical Journal
1996;
313
(7057):608.

4
Coggon D, Barker D, Rose G.
Epidemiology for the uninitiated
. London: BMJ Books, 2009.

5
Cuff A. Sources of Bias in Clinical Trials. 2013.
http://applyingcriticality.wordpress.com/2013/06/19/sources-of-bias-in-clinical-trials/
(accessed 26th June 2013).

6
Delgado-Rodríguez M, Llorca J. Bias.
Journal of Epidemiology and Community Health
2004;
58
(8):635–41 doi: 10.1136/jech.2003.008466.

7
Britton A, McKee M, Black N, et al. Choosing between randomised and non-randomised studies: a systematic review.
Health Technology Assessment (Winchester, England)
1998;
2
(13):i.

8
Rimm EB, Williams P, Fosher K, et al. Moderate alcohol intake and lower risk of coronary heart disease: meta-analysis of effects on lipids and haemostatic factors.
BMJ: British Medical Journal
1999;
319
(7224):1523.

9
Fillmore KM, Stockwell T, Chikritzhs T, et al. Moderate alcohol use and reduced mortality risk: systematic error in prospective studies and new hypotheses.
Annals of Epidemiology
2007;
17
(5):S16–23.

10
Ronksley PE, Brien SE, Turner BJ, et al. Association of alcohol consumption with selected cardiovascular disease outcomes: a systematic review and meta-analysis.
BMJ: British Medical Journal
2011;
342
:d671.

11
Stockwell T, Greer A, Fillmore K, et al. How good is the science?
BMJ: British Medical Journal
2012;
344
:e2276.

12
Bowie C. Lessons from the pertussis vaccine court trial.
Lancet
1990;
335
(8686), 397–399.

13
Gawande A.
Complications: a surgeon's notes on an imperfect science
. London: Profile Books, 2010.

14
Sackett DL, Haynes RB, Tugwell P.
Clinical epidemiology: a basic science for clinical medicine
. Boston, USA: Little, Brown and Company, 1985.

15
Majeed A, Troy G, Smythe A, et al. Randomised, prospective, single-blind comparison of laparoscopic versus small-incision cholecystectomy.
The Lancet
1996;
347
(9007):989–94.

16
MRC Working Party. Medical Research Council trial of treatment of hypertension in older adults: principal results.
BMJ: British Medical Journal
1992;
304
:405–12.

17
Diao D, Wright JM, Cundiff DK, et al. Pharmacotherapy for mild hypertension.
Cochrane Database of Systematic Reviews (Online)
2012;
8
:CD006742 doi: 10.1002/14651858.CD006742.pub2.

18
Spence D. Why do we overtreat hypertension?
BMJ: British Medical Journal
2012;
345
:e5923 doi: 10.1136/bmj.e5923.

19
Charles P, Giraudeau B, Dechartres A, et al. Reporting of sample size calculation in randomised controlled trials: review.
BMJ: British Medical Journal
2009;
338
:b1732.

20
Machin D, Campbell MJ, Tan S-B, et al.
Sample size tables for clinical studies
. Oxford: Wiley-Blackwell, 2011.

Chapter 5

Statistics for the non-statistician

How can non-statisticians evaluate statistical tests?

In this age where medicine leans increasingly on mathematics, no clinician can afford to leave the statistical aspects of a paper entirely to the ‘experts’. If, like me, you believe yourself to be innumerate, remember that you do not need to be able to build a car in order to drive one. What you do need to know about statistical tests is which is the best test to use for common types of statistical questions. You need to be able to describe
in words
what the test does and in what circumstances it becomes invalid or inappropriate. Box 5.1 shows some frequently used ‘tricks of the trade’, which all of us need to be alert to (in our own as well as other people's practice).

The summary checklist in Appendix 1, explained in detail in the subsequent sections, constitute my own method for assessing the adequacy of a statistical analysis, which some readers will find too simplistic. If you do, please skip this section and turn either to a more comprehensive presentation for the non-statistician: the ‘Basic Statistics for Clinicians’ series in the
Canadian Medical Association Journal
[1–4], or to a more mainstream statistical textbook. When I asked my Twitter followers which statistics textbook they preferred, the post popular ones were these [5–7]. If you find statistics impossibly difficult, take these points one at a time and return to read the next point only when you feel comfortable with the previous ones. None of the points presupposes a detailed knowledge of the actual calculations involved.

The first question to ask, by the way, is, ‘Have the authors used any statistical tests at all?’ If they are presenting numbers and claiming that these numbers mean something, without using statistical methods to prove it, they are almost certainly skating on thin ice.

Box 5.1 Ten ways to cheat on statistical tests when writing up results

1.
Throw all your data into a computer and report as significant any relationship where ‘
p
< 0.05’ (see section ‘Have “p-values” been calculated and interpreted appropriately?’).

2.
If baseline differences between the groups favour the intervention group, remember not to adjust for them (see section ‘Have they determined whether their groups are comparable, and, if necessary, adjusted for baseline differences?’).

3.
Do not test your data to see if they are normally distributed. If you do, you might be stuck with non-parametric tests, which aren't as much fun (see section ‘What sort of data have they got, and have they used appropriate statistical tests?’).

4.
Ignore all withdrawals (‘drop outs’) and non-responders, so the analysis only concerns subjects who fully complied with treatment (see section ‘Were preliminary statistical questions addressed?’).

5.
Always assume that you can plot one set of data against another and calculate an ‘
r
-value’ (Pearson correlation coefficient) (see section ‘Has correlation been distinguished from regression, and has the correlation coefficient (‘
r
-value’) been calculated and interpreted correctly?’), and that a ‘significant’
r
-value proves causation (see section ‘Have assumptions been made about the nature and direction of causality?’).

6.
If outliers (points that lie a long way from the others on your graph) are messing up your calculations, just rub them out. But if outliers are helping your case, even if they appear to be spurious results, leave them in (see section ‘Were ‘outliers’ analysed with both common sense and appropriate statistical adjustments?’).

7.
If the confidence intervals of your result overlap zero difference between the groups, leave them out of your report. Better still, mention them briefly in the text but don't draw them in on the graph and ignore them when drawing your conclusions (see section ‘Have confidence intervals been calculated, and do the authors' conclusions reflect them?’).

8.
If the difference between two groups becomes significant 4.5 months into a 6-month trial, stop the trial and start writing up. Alternatively if at 6 months, the results are ‘nearly significant’, extend the trial for another 3 weeks (see section ‘Have the data been analysed according to the original study protocol?’).

9.
If your results prove uninteresting, ask the computer to go back and see if any particular sub-groups behaved differently. You might find that your intervention worked after all in Chinese women aged 52–61 (see section ‘Have the data been analysed according to the original study protocol?’).

10.
If analysing your data the way you plan to does not give the result you wanted, run the figures through a selection of other tests (see section ‘If the statistical tests in the paper are obscure, why have the authors chosen to use them, and have they included a reference?’).

Have the authors set the scene correctly?

Have they determined whether their groups are comparable, and, if necessary, adjusted for baseline differences?

Most comparative clinical trials include either a table or a paragraph in the text showing the baseline characteristics of the groups being studied (i.e. their characteristics
before
the trial or observational study was begun). Such a table should demonstrate that both the intervention and control groups are similar in terms of age and sex distribution and key prognostic variables (such as the average size of a cancerous lump). If there are important differences in these baseline characteristics, even though these may be due to chance, it can pose a challenge to your interpretation of results. In this situation, you can carry out certain adjustments to try to allow for these differences and hence strengthen your argument. To find out how to make such adjustments, see the relevant section in any of the mainstream biostatistics textbooks—but don't try to memorise the formulae!

What sort of data have they got, and have they used appropriate statistical tests?

Numbers are often used to label the properties of things. We can assign a number to represent our height, weight and so on. For properties like these, the measurements can be treated as actual numbers. We can, for example, calculate the average weight and height of a group of people by averaging the measurements. But consider a different example, in which we use numbers to label the property ‘city of origin’, where 1, London, 2, Manchester, 3, Birmingham and so on. We could still calculate the average of these numbers for a particular sample of cases but the result would be meaningless. The same would apply if we labelled the property ‘liking for
x
’, with 1, not at all, 2, a bit and 3, a lot. Again, we could calculate the ‘average liking’ but the numerical result would be uninterpretable unless we knew that the difference between ‘not at all’ and ‘a bit’ was exactly the same as the difference between ‘a bit’ and ‘a lot’.

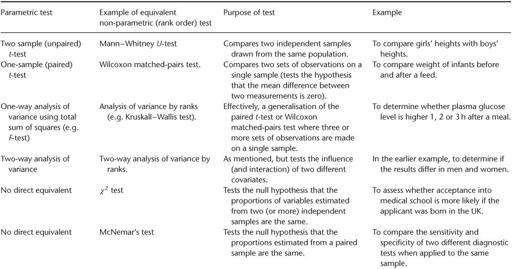
The statistical tests used in medical papers are generally classified as either parametric (i.e. they assume that the data were sampled from a particular form of distribution, such as a normal distribution) or non-parametric (i.e. they do not assume that the data were sampled from a particular type of distribution).

The non-parametric tests focus on the
rank order
of the values (which one is the smallest, which one comes next, etc.), and ignore the absolute differences between them. As you might imagine, statistical significance is more difficult to demonstrate with rank order tests (indeed, some statisticians are cynical about the value of the latter), and this tempts researchers to use statistics such as the
r
-value (see section ‘Has correlation been distinguished from regression, and has the correlation coefficient (“
r
-value”) been calculated and interpreted correctly?’) inappropriately. Not only is the
r
-value (parametric) easier to calculate than an equivalent rank order statistic such as Spearman's
ρ
(pronounced ‘rho’) but it is also much more likely to give (apparently) significant results. Unfortunately, it will also give an entirely spurious and misleading estimate of the significance of the result, unless the data are appropriate to the test being used. More examples of parametric tests and their rank order equivalents (if present) are given in
Table 5.1
.

Table 5.1
Some commonly used statistical tests