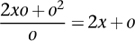Read In Pursuit of the Unknown Online
Authors: Ian Stewart
In Pursuit of the Unknown (9 page)
When the plague died down, he told no one about the discoveries he had made. He returned to Cambridge, took a master's degree, and became a fellow at Trinity. Elected to the Lucasian Chair of Mathematics, he finally began to publish his ideas and to develop new ones.
The young man was Isaac Newton. His discoveries created a revolution in science, bringing about a world that Charles II would never have believed could exist: buildings with more than a hundred floors, horseless carriages doing 80 mph along the M6 motorway while the driver listens to music using a magic disc made from a strange glasslike material, heavier-than-air flying machines that cross the Atlantic in six hours, colour pictures that move, and boxes you carry in your pocket that talk to the other side of the world . . .
Previously, Galileo Galilei, Johannes Kepler, and others had turned up the corner of nature's rug and seen a few of the wonders concealed beneath it. Now Newton cast the rug aside. Not only did he reveal that the universe has secret patterns, laws of nature; he also provided mathematical tools to express those laws precisely and to deduce their consequences. The system of the world was mathematical; the heart of God's creation was a soulless clockwork universe.
The world view of humanity did not suddenly switch from religious to secular. It still has not done so completely, and probably never will. But after Newton published his
Philosophiæ Naturalis Principia Mathematica
(âMathematical Principles of Natural Philosophy') the âSystem of the World' â the book's subtitle â was no longer solely the province of organised religion. Even so, Newton was not the first modern scientist; he had a mystical side too, devoting years of his life to alchemy and religious speculation. In notes for a lecture
1
the economist John Maynard Keynes, also a Newtonian scholar, wrote:
Newton was not the first of the age of reason. He was the last of the magicians, the last of the Babylonians and Sumerians, the last great mind which looked out on the visible and intellectual world with the same eyes as those who began to build our intellectual inheritance rather less than 10,000 years ago. Isaac Newton, a posthumous child born with no father on Christmas Day, 1642, was the last wonderchild to whom the Magi could do sincere and appropriate homage.
Today we mostly ignore Newton's mystic aspect, and remember him for his scientific and mathematical achievements. Paramount among them are his realisation that nature obeys mathematical laws and his invention of
calculus, the main way we now express those laws and derive their consequences. The German mathematician and philosopher Gottfried Wilhelm Leibniz also developed calculus, more or less independently, at much the same time, but he did little with it. Newton used calculus to understand the universe, though he kept it under wraps in his published work, recasting it in classical geometric language. He was a transitional figure who moved humanity away from a mystical, medieval outlook and ushered in the modern rational world view. After Newton, scientists consciously recognised that the universe has deep mathematical patterns,
and
were equipped with powerful techniques to exploit that insight.
The calculus did not arise âout of the blue'. It came from questions in both pure and applied mathematics, and its antecedents can be traced back to Archimedes. Newton himself famously remarked, âIf I have seen a little further it is by standing on the shoulders of giants.'
2
Paramount among those giants were John Wallis, Pierre de Fermat, Galileo, and Kepler. Wallis developed a precursor to calculus in his 1656
Arithmetica Infinitorum
(âArithmetic of the Infinite'). Fermat's 1679
De Tangentibus Linearum Curvarum
(âOn Tangents to Curved Lines') presented a method for finding tangents to curves, a problem intimately related to calculus. Kepler formulated three basic laws of planetary motion, which led Newton to his law of gravity, the subject of the next chapter. Galileo made big advances in astronomy, but he also investigated mathematical aspects of nature down on the ground, publishing his discoveries in
De Motu
(âOn Motion') in 1590. He investigated how a falling body moves, finding an elegant mathematical pattern. Newton developed this hint into three general laws of motion.
To understand Galileo's pattern we need two everyday concepts from mechanics: velocity and acceleration. Velocity is how fast something is moving, and in which direction. If we ignore the direction, we get the body's speed. Acceleration is a change in velocity, which usually involves a change in speed (an exception arises when the speed remains the same but the direction changes). In everyday life we use acceleration to mean speeding up and deceleration for slowing down, but in mechanics both changes are accelerations: the first positive, the second negative. When we drive along a road the speed of the car is displayed on the speedometer â it might, for instance, be 50 mph. The direction is whichever way the car is pointing. When we put our foot down, the car accelerates and the speed
increases; when we stamp on the brakes, the car decelerates â negative acceleration.
If the car is moving at a fixed speed, it's easy to work out what that speed is. The abbreviation mph gives it away: miles per hour. If the car travels 50 miles in 1 hour, we divide the distance by the time, and that's the speed. We don't need to drive for an hour: if the car goes 5 miles in 6 minutes, both distance and time are divided by 10, and their ratio is still 50 mph. In short,
speed = distance travelled divided by time taken.
In the same way, a fixed rate of acceleration is given by
acceleration = change in speed divided by time taken.
This all seems straightforward, but conceptual difficulties arise when the speed or acceleration is not fixed. And they can't both be constant, because constant (and nonzero) acceleration implies a changing speed. Suppose you drive along a country lane, speeding up on the straights, slowing for the corners. Your speed keeps changing, and so does your acceleration. How can we work them out at any given instant of time? The pragmatic answer is to take a short interval of time, say a second. Then your instantaneous speed at (say) 11.30 am is the distance you travel between that moment and one second later, divided by one second. The same goes for instantaneous acceleration.
Except . . . that's not quite your
instantaneous
speed. It's really an average speed, over a one-second interval of time. There are circumstances in which one second is a
huge
length of time â a guitar string playing middle C vibrates 440 times every second; average its motion over an entire second and you'll think it's standing still. The answer is to consider a shorter interval of time â one ten thousandth of a second, perhaps. But this still doesn't capture instantaneous speed. Visible light vibrates one quadrillion (10
15
) times every second, so the appropriate time interval is less than one quadrillionth of a second. And even then . . . well, to be pedantic, that's still not an
instant
. Pursuing this line of thought, it seems to be necessary to use an interval of time that is shorter than any other interval. But the only number like that is 0, and that's useless, because now the distance travelled is also 0, and 0/0 is meaningless.
Early pioneers ignored these issues and took a pragmatic view. Once the probable error in your measurements exceeds the increased precision you would theoretically get by using smaller intervals of time, there's no point in doing so. The clocks in Galileo's day were very inaccurate, so he
measured time by humming tunes to himself â a trained musician can subdivide a note into very short intervals. Even then, timing a falling body is tricky, so Galileo hit on the trick of slowing the motion down by rolling balls down an inclined slope. Then he observed the position of the ball at successive intervals of time. What he found (I'm simplifying the numbers to make the pattern clear, but it's the same pattern) is that for times 0, 1, 2, 3, 4, 5, 6, . . . these positions were
0 1 4 9 16 25 36
The distance was (proportional to) the square of the time. What about the speeds? Averaged over successive intervals, these were the differences
1 3 5 7 9 11
between the successive squares. In each interval, other than the first, the average speed increased by 2 units. It's a striking pattern â all the more so to Galileo when he dug something very similar out of dozens of measurements with balls of many different masses on slopes with many different inclinations.
From these experiments and the observed pattern, Galileo deduced something wonderful. The path of a falling body, or one thrown into the air, such as a cannonball, is a parabola. This is a U-shaped curve, known to the ancient Greeks. (The U is upside down in this case. I'm ignoring air resistance, which changes the shape: it didn't have much effect on Galileo's rolling balls.) Kepler encountered a related curve, the ellipse, in his analysis of planetary orbits: this must have seemed significant to Newton too, but that story must wait until the next chapter.
With only this particular series of experiments to go on, it's not clear what general principles underlie Galileo's pattern. Newton realised that the source of the pattern is rates of change. Velocity is the rate at which position changes with respect to time; acceleration is the rate at which velocity changes with respect to time. In Galileo's observations, position varied according to the square of time, velocity varied linearly, and acceleration didn't vary at all. Newton realised that in order to gain a deeper understanding of Galileo's patterns, and what they meant for our view of nature, he had to come to grips with instantaneous rates of change. When he did, out popped calculus.
You might expect an idea as important as calculus to be announced with a fanfare of trumpets and parades through the streets. However, it takes time
for the significance of novel ideas to sink in and to be appreciated, and so it was with calculus. Newton's work on the topic dates from 1671 or earlier, when he wrote
The Method of Fluxions and Infinite Series
. We are unsure of the date because the book was not published until 1736, nearly a decade after his death. Several other manuscripts by Newton also refer to ideas that we now recognise as differential and integral calculus, the two main branches of the subject. Leibniz's notebooks show that he obtained his first significant results in calculus in 1675, but he published nothing on the topic until 1684.
After Newton had risen to scientific prominence, long after both men had worked out the basics of calculus, some of Newton's friends sparked a largely pointless but heated controversy about priority, accusing Leibniz of plagiarising Newton's unpublished manuscripts. A few mathematicians from continental Europe responded with counter-claims of plagiarism by Newton. English and continental mathematicians were scarcely on speaking terms for a century, which caused huge damage to English mathematicians, but none whatsoever to the continental ones. They developed calculus into a central tool of mathematical physics while their English counterparts were seething about insults to Newton instead of exploiting insights from Newton. The story is tangled and still subject to scholarly disputation by historians of science, but broadly speaking it seems that Newton and Leibniz discovered the basic ideas of calculus independently â at least, as independently as their common mathematical and scientific culture permitted.
Leibniz's notation differs from Newton's, but the underlying ideas are more or less identical. The intuition behind them, however, is different. Leibniz's approach was a formal one, manipulating algebraic symbols. Newton had a physical model at the back of his mind, in which the function under consideration was a physical quantity that varies with time. This is where his curious term âfluxion' comes from â something that flows as time passes.
Newton's method can be illustrated using an example: a quantity
y
that is the square
x
2
of another quantity
x
. (This is the pattern that Galileo found for a rolling ball: its position is proportional to the square of the time that has elapsed. So there
y
would be position and
x
time. The usual symbol for time is
t
, but the standard coordinate system in the plane uses
x
and
y
.) Start by introducing a new quantity
o
, denoting a small change in
x
. The corresponding change in
y
is the difference
(
x
+
o
)
2
â
x
2
which simplifies to 2
xo
+
o
2
. The rate of change (averaged over a small interval of length
o
, as
x
increases to
x
+ o) is therefore