Letters to a Young Mathematician (15 page)
Read Letters to a Young Mathematician Online
Authors: Ian Stewart
Page
and baffled by open questions like the Riemann hypothesis.
The Riemann hypothesis concerns Riemann’s zeta function ζ (
z
), which makes it possible to convert questions about prime numbers into questions in complex analysis. It states that if ζ (
z
) is zero then either
z
is twice a negative integer or the real part of
z
is ½. See Karl Sabbagh,
Dr. Rie-mann’s
Zeros
, Atlantic Books, London 2002.
Page
the prevalent belief that the human sperm count is
falling.
P. Bromwich, J. Cohen, I. Stewart, and A. Walker, Decline in sperm counts: An artefact of changed reference range of “normal”?
British Medical
Journal
309 (2 July 1994) 19–22.
Page
Leonardo of Pisa, also known as Fibonacci.
“Fibonacci” means “son of Bonaccio.” This nickname was probably invented by Guillaume Libri in the nineteenth century, and certainly does not go back much earlier.
Page
the only plausible symmetric network that could explain
all of the standard gaits of four-legged animals.
M. Golubitsky, I. Stewart, J. J. Collins, and P.-L.
Buono, Symmetry in locomotor central pattern generators and animal gaits,
Nature
401 (1999) 693–695.
Page
as some say the Bible does, but only if you take an obscure
passage extremely literally.
1 Kings 7:23 reads, “And he [Hiram on behalf of King Solomon] made a molten sea, ten cubits from the one brim to the other: it was round all about, and his height was five cubits: and a line of thirty cubits did compass it round about.” If we assume the geometry is a circle, and if we assume the measurements are exact, then the circumference is three times the diameter: π = 3. But the passage is clearly not intended as a precise mathematical statement.
Page
Mission to Abisko
. Mission to Abisko
(eds. J. Casti and A. Karlqvist), Perseus, New York 1999, 157–185.
Page
Occasionally someone invents such a piece of machinery
out of the blue, and proves all the experts wrong.
A classic case is Louis De Branges’s proof of the Bieberbach conjecture. See Ian Stewart,
From
Here to Infinity
, Oxford University Press, Oxford 1996, 206.
Page
Sir Peter Swinnerton-Dyer, has offered a simpler explanation
of Fermat’s claim.
P. Swinnerton-Dyer, The justification of mathematical statements,
Philosophical
Transactions of the Royal Society of London
Series A 363 (2005), 2437–2447.
Page
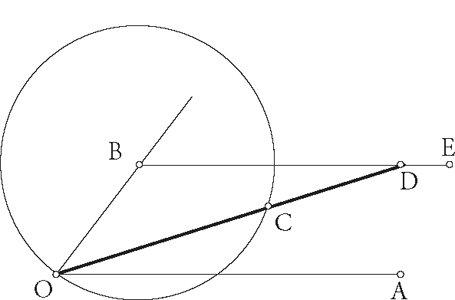
Archimedes knew how to trisect an angle using a
marked
ruler and compass
. Given angle AOB, draw BE parallel to OA, and the circle center B through O whose radius equals CD, where C and D are the marks on the ruler (thick line). Place the ruler so that it passes through O, while C lies on the circle and D lies on BE. Then angle AOC is one-third of angle AOB. See Underwood Dudley,
A Budget of Trisections
, Springer, New York 1987.
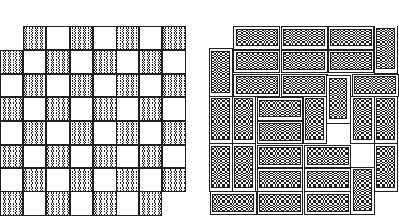
Page
given a chessboard with two diagonally opposite corners
missing, can you cover it with thirty-one dominoes?
The left figure shows the chessboard with its missing corners. The right figure shows a typical attempt to cover it: two squares are left uncovered.
In contrast, if the two missing corners are adjacent to each other, then the puzzle is easily solved:
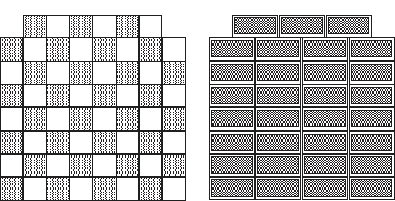
Page
it is impossible to trisect the angle using an unmarked
straightedge and compass.
The first proof was given by Wantzel. See Ian Stewart,
Galois Theory
, Chapman and Hall /CRC, Boca Raton 2004.
Page
a short calculation shows that with rare exceptions, the
cubic equation associated with angle trisection is not like
that.
Ian Stewart,
Galois Theory
, Chapman and Hall /CRC, Boca Raton 2004.
Page
Mathematicians are proud to trace their academic lineage
through thesis advisers.
There is a website dedicated to doing just that:
http://www.genealogy.ams.org/
Page
All of my Portuguese daughters have remained in mathematics.
The story of the first, Isabel Labouriau, is one of the many fascinating biographical histories in a wonderful book about women in mathematics:
Complexities
(eds. Betty Anne Case and Anne M. Leggett), Princeton University Press, Princeton 2005.
Page
a penetrating article in 1981 in
Mathematics Tomorrow. Timothy Poston, Purity in applications, in
Mathematics Tomorrow
(ed. L. A. Steen), Springer, New York 1981, 49–54.
Page
such gems as the law of quadratic reciprocity.
This theorem, first proved by Gauss, states that if
p
and
q
are odd primes, then the equation
x
2
=
mp
+
q
has
a solution in integers if and only if the related equation
y
2
=
nq
+
p
has a solution, except that if both
p
and
q
are of the form 4
k
+ 3, then one equation has a solution and the other does not. See G. A. Jones and J. M. Jones,
Elementary Number Theory
, Springer, London 1998.
Page
the Titius–Bode law.
This empirical pattern in the spacing of the planets was discovered by Johann Titius in 1766 and published by Johann Bode in 1772. Take the series 0, 3, 6, 12, 24, 48, 96, in which each number except the first is twice the preceding number. Add 4 to each term and divide by 10, to get 0.4, 0.7, 1.0, 1.6, 2.8, 5.2, 10.0. Omitting 2.8, these are very close to the distances from the sun to Mercury, Venus, Earth, Mars, Jupiter, and Saturn, respectively, measured in astronomical units. (By definition, the distance from Earth to the sun is one astronomical unit.) The asteroid Ceres neatly filled the gap at 2.8.
Page
Karl Weierstrass found a simple continuous function
that is differentiable
nowhere
.
K. Falconer,
Fractal
Geometry
, Wiley, New York 1990.
Page
On the Enfeeblement of Mathematical Skills
. J. Hammersley. On the enfeeblement of mathematical skills by “Modern Mathematics” and by similar soft intellectual trash in schools and universities,
Bulletin of the Institute of Mathematics and its Applications
4 (1960) 66.
Page
his “shape of a drum” paper is a gem.
M. Kac. Can one hear the shape of a drum?
American Mathematical
Monthly
73 (1966) 1–23. Given the spectrum of tones that can be produced by a vibrating membrane
in the plane, can you deduce its shape? Kac proved that its area and perimeter can be deduced. The general question was answered in the negative by C. Gordon, D. Webb, and S. Wolpert, One can’t hear the shape of a drum,
Bulletin of the American
Mathematical Society
27 (1992) 134–138.
Page
Hammersley’s 2004 obituary in the
Independent on Friday
. Independent on Friday,
14 May 2004.
Page
John Barrow argues the case like this. Mission to
Abisko
(eds. J. Casti and A. Karlqvist), Perseus, New York 1999, 3–12.
Page
The Man Who Knew Infinity. Robert Kanigel,
The Man Who Knew Infinity
, Scribner’s, New York 1991.
Page
Grisha Perelman’s alleged proof of the Poincaré conjecture.
J. Milnor, Towards the Poincaré conjecture and the classification of 3-manifolds,
Notices of
the American Mathematical Society
50 (2003) 1226–1233, and M. T. Anderson, Geometrization of manifolds via the Ricci flow,
Notices of the American
Mathematical Society
51 (2004) 184–193.