Mathematics and the Real World (41 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein
The rows in the table represent the possibilities, that is, the strategies, facing the first suspect, and the columns represent those of the second suspect. The top row shows the position when the first suspect testifies against the second, and the second row is the situation when he refuses to do so. The left column shows the position when the second suspect refuses to testify and continues to plead not guilty, the right shows when he agrees to testify against the first. The two numbers in the cells of the table show the number of years each suspect will be sentenced to as a result of their decisions; the number on the left refers to the first suspect, and that on the right refers to the second.
The reader will readily see that the table reflects what was described above verbally. Each suspect wants to minimize the number of years he will have to spend in prison. When the concepts described above are applied, it is easy to see that testifying against the other suspect is the dominant strategy for each of them. In other words, for each suspect, testifying against the other is worthwhile, regardless of what the other decides to do. Specifically, the pair of strategies in which each suspect agrees to testify is in equilibrium. According to our description of dominant strategies above, we have solved the game. Each suspect will agree to testify against the other, and the outcome will be that each will serve a three-year sentence,
whereas if neither had agreed to testify they would each have served only one year.
Have we then solved the game correctly? We will return to this question further on, and here we will note that we have solved the mathematical game, but the mathematical game ignores many aspects of conflicts that we come across in our daily lives.
The second game is known as the
battle of the sexes
. Presented in table form, it looks as follows:
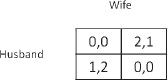
The situation is that a husband and wife have agreed to go out together that evening. He would prefer a football game as their joint destination, and she would prefer them to go to the opera (the rows represent the husband and the columns the wife). Both would prefer to spend the evening together and not go to different events. As in the previous table, the left number in each cell is the “return” to whoever is represented in the rows, in this case the husband, and the right number in each cell is the return to the wife (represented in the columns). Each one would like to obtain as high a return as possible. It can easily be seen that in this game there are two possible results that are in equilibrium: either to go together to the football game or to go together to the opera. The mathematics does not indicate which of these is the better choice.
The third game is a version of the common and familiar
heads or tails
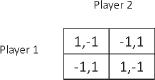
. One player writes down his choice of heads or tails, without revealing his choice to the other player. The second player has to guess the choice of the first. If he guesses correctly the first player pays him, say, one dollar. If he guesses wrongly, he pays the other player one dollar. In this game the table looks like this
It can be proven quite simply that in this game there are no equilibrium strategies. This game is also called a zero-sum or fixed-sum game, as the payoffs merely pass from one player to the other. As can be seen in the table, the sum of the payoffs in each cell is zero, namely, the gain of one player is the loss of the other.
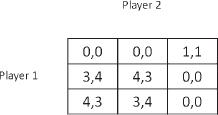
We have shown three games in one of which there was one equilibrium, in the second there were two equilibrium outcomes, and in the third, none. The explanation of equilibrium given previously still holds to some extent. For example, in the battle of the sexes, if the husband and wife agreed to meet at the opera, it would make no sense for one of them to arrive at the second performance without coordinating that in advance with the other. Game theory has no answer to the question of whether the opera or a football game is preferable; it does not rate the two options, per se. Neither does game theory recommend the adoption of an equilibrium strategy, even if it is the only one. Here is a table of a game that reflects this.
The numbers in the cells indicate, say, monetary payoffs. The strategy in which the first player chooses the upper row and the second player chooses the right column are the only ones in equilibrium, although it is
clear that if the players restrict themselves to choosing the other rows and columns, the situation of both of them will improve, and moreover there will be no incentive for them to revert to their initial strategies.
Game theory developed another course of action for players in games presented in strategic form, and that is to use a
mixed strategy
, something that children do naturally when playing heads or tails. To prevent his rival from revealing whether he has chosen heads or tails, he flips a coin so that his choice is a random one. The mathematical expression of this is deciding not on a particular strategy but on a draw in which the chosen strategy is drawn according to the distribution of the chances that the player determines. In such a case what is the payoff? The actual result will be determined only once all the draws have taken place and it is then known which strategies were drawn in the lottery. At the decision stage the player knows only what lottery he has chosen, and likewise for the other players. For the purpose of deciding which lottery to choose, we determine that the outcome of the game will be the expectation (in the probabilistic sense) of payoffs, the expectation according to the chances that the players have determined. Although ultimately the player will receive the payoff that is the result of the various lotteries, the assumption is that at the stage of deciding on the lottery between the various strategies, the player is interested in achieving the highest possible expectation. We will examine this assumption in the next section.
As we noted, the concept of mixed strategies was introduced by Émile Borel, who also showed how to calculate such strategies in equilibrium for many instances of zero-sum games, but he did not believe that it was possible to solve all games in this way. John von Neumann, however, proved that in such games mixed strategies that were in equilibrium could always be found. The expectation of the payoffs is then the same in all the equilibrium states, independent of which equilibrium strategy is chosen, and that payoff is known as the value of the game. This is known as the minimax (or minmax) theorem, because the strategy minimizes the possible loss by each of the two players separately, leading to an equilibrium outcome. In the heads or tails game, the value is zero and the strategies selected by
children, that is, to choose heads or tails with equal probabilities, are in fact in equilibrium. John Nash went further and proved that in every strategic game (that is a game in which every player has a finite number of strategies) there are mixed strategies that are in equilibrium.
If we adopt the possibility of mixed strategies, not only is it certain that an equilibrium exists, but in certain situations possibilities of reaching a more reasonable equilibrium arise. For example, we explained why the equilibrium in the 3 × 3 table above is not reasonable as a solution to the game, although it is the only equilibrium. If we allow mixed strategies, and assuming that the players want to maximize their expected payoffs, a new equilibrium comes to light. This is obtained when each player chooses one of the other options, that is, the two lower rows in the case of the first player, and the two left columns in the case of the second, with equal probabilities.
Note that by using mixed strategies we have moved from a situation in which a player receives an actual payoff, whether monetary, or the number of years in prison, or what have you, to a situation where the payoff is a lottery between several possible actual payoffs. In the next three sections we will discuss people's attitudes to states of uncertainty, and in particular to the use of lotteries.
Sometimes the suggestion to look for an equilibrium strategy causes unease, for example in the case of the prisoner's dilemma. On the abstract level we agreed that if a player has a dominant strategy he will use it. In similar day-to-day situations, however, we find it worthwhile to cooperate rather than to opt for the dominant strategy. The reasons for such a choice in normal daily life are not reflected in the limited model we presented. For example, our model does not take into consideration what friends of the suspect sentenced to years in jail are likely to do to the suspect who betrayed his partner in crime. This is a clear illustration of the fact that the mathematical game lacks very important elements that decision makers must take into account. Researchers were not unaware of this aspect, and they put forward models that take into account responses that are outside the table itself. One of the models allows an unlimited or unknown number
of repeats of the game, so that every suspect will take into consideration future decisions of the other suspect, decisions that are likely to include retaliation for the current lack of cooperation. The analysis of such repeated games was one of the judges’ reasons in the citation awarding the Nobel Prize in Economics in 2005 to the mathematician Robert J. Aumann of the Hebrew University of Jerusalem.
The concepts of game theory have been included in other areas, such as economics, in which the distribution of resources takes place via markets that bring prices of the different products into equilibrium. Such a model was proposed by Kenneth Arrow, whom we mentioned earlier, and Gérard Debreu (1921–2004), a mathematical economist of the University of California, Berkeley, who was awarded the Nobel Prize in Economics in 1983.
As a result of these developments, the concept of equilibrium as well as other concepts developed in game theory, such as a zero-sum game, became part of general public discourse, although the participants in the discussion do not always draw the appropriate conclusions. For example, the incentives for people or companies to honor signed agreements are the punishments incurred if they breach the agreement, whether punishments are imposed by the courts, such as prison sentences or fines, or by future boycotts. In the absence of any retribution or expected punishment for infringement, an agreement is no more than a statement of intention, and it will be broken as soon as it is worthwhile for one of the parties to do so. Therefore, in cases where there is no system of punishment, as in many international agreements, it is up to the parties to the agreement to see to it that, as far as possible, the agreements themselves should have the property of Nash's equilibrium. In other words, no party to the agreement should benefit by breaching it unilaterally. Despite this elementary insight that originates from game theory, it does not appear that politicians who are signatories to agreements, sometimes fateful agreements, even try to take this into consideration.