Mathematics and the Real World (67 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein
Teacher:
Now we square both sides of the equation, and we get 2 =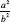 , or
, or
a
2
= 2
b
2
. So
a
is even, and can be written as 2
c
.
Student:
Fine.
Teacher:
Substitute 2
c
in the previous equation, and we get 4
c
2
= 2
b
2
. Dividing both sides by 2 leads to the conclusion that
b
is also even. But we started by justifying the assumption that either
a
or
b
must be odd. We have arrived at a contradiction.
Student:
So what?
Teacher:
The contradiction derived from the assumption that the square root of 2 is rational.
Student:
I said at the beginning that we couldn't assume that.
The above was an imaginary conversation, but similar ones take place very often in the study of mathematics. The difficulty that it reflects derives
from the fact that the teacher has become accustomed to the argument, may have taught the proof many times, and has simply forgotten the basic difficulty based on proof by contradiction. We should be aware of and remember the obstacles the proof had to overcome among the Pythagoreans, who concealed it for many years for reasons of their own, and it may well be that they did so because the proof is not easy to understand. We should also remember that even in the twentieth century there were those who argued against the method of proof by contradiction. The objections to the method would not have arisen if such proofs were obvious, that is, if they were compatible with intuition. I am not suggesting that young students be exposed to the tradition that views such proofs as problematic, but the recognition that such proofs can be memorized but are difficult to absorb should be reflected in the way they are taught. This difficulty cannot be completely overcome. The best way to deal with it is to separate the explanation of the principle underlying these claims from the proof itself, to be patient, and not to expect the student to arrive at such claims by himself.
The student will encounter similar difficulties in understanding claims containing logical quantifiers such as “all,” “there exists” or “there does not exist.” For example, if the teacher proves that a certain property, say of triangles, holds for all triangles, he cannot expect that henceforth the student will use such knowledge. The lack of accessibility to a fact that has already been proven is not due to the student possibly forgetting that property but is the result of the fact that the claim “all” does not sit naturally in the human brain. The student will face the same difficulty when the teacher uses the third of the classic rules of thought, the rule of the excluded middle (“either P [the proposition] is true or its negation is true”). The use of this rule is not intuitive. The only way to succeed in using it is to isolate it, and to draw attention to it whenever using it, and lessons must be planned accordingly.
One of the central difficulties deriving from the way the brain works is its failure to relate to stipulations or conditions. The mind does not think conditionally and generally does not discover that it lacks data required for an analysis of the situation. Evolution trained us to complete an incomplete
picture somehow or other. A delay intended to enable the brain to discover the missing condition could have had dire results for the human race in the course of evolution, as a result of which, today we usually skip that stage. In mathematics the result is likely to lead to errors. I will illustrate with an example from probability studies.
We described the logical approach to probability and difficulties arising from it in sections 40 to 43. We will now see how experienced teachers are exposed to errors. It must be stressed, the example is not given to illustrate the error or to embarrass or belittle the writer of the article we shall analyze. We give the example in detail because we think that, in that way, we can identify the source of the error, which is the difficulty in identifying provisions and the completion of the picture by the brain. We will extend the discussion and go into detail in order to emphasize the refinement required in analyzing such problems.
The title of the article that appeared in a teacher's magazine some years ago was a promising one: “Conditional Probability as a Source of Paradoxes and Surprising Results.” The introduction was in the same vein: “Mathematical thinking is an important means for discovering the world…. Phenomena that seem mysterious and paradoxical are explained rationally…,” and so on. The article itself gave examples of apparent paradoxes, which it then explains rationally, apparently. Here is one of the examples.
Boys and girls
. We are given that the probability of the birth of a son is . A certain family has three children. The example has two stages. The first is that outside their apartment we see two girls of that family. What is the probability that the other child is a boy? The second stage is that in addition to the two girls, we can see the outline of a baby, in the apartment, a younger brother or sister of the two girls we met. What then is the probability that the third child is a boy?
. A certain family has three children. The example has two stages. The first is that outside their apartment we see two girls of that family. What is the probability that the other child is a boy? The second stage is that in addition to the two girls, we can see the outline of a baby, in the apartment, a younger brother or sister of the two girls we met. What then is the probability that the third child is a boy?
The approach of the article to the answer to the question is flawed. We will show the answer given in the article and will then point out the error. We reemphasize: it is not our purpose to belittle the author of the article. Errors are standard fare in mathematics. Our objective is to indicate the source of the error. First we will show the solution given in the article.
The writer solves the exercise only after stating that many students are convinced that the answer to the first part of the question is . Their explanation, he claims, is that because of symmetry: the chance that the third child is a boy is equal to the chance that it is a girl. Then the author gives the “right” answer. He assigns the number 1 to a male child, and 0 to a female child. With the help of these symbols we can record eight three-digit permutations that describe all the possible situations for the three-child family:
. Their explanation, he claims, is that because of symmetry: the chance that the third child is a boy is equal to the chance that it is a girl. Then the author gives the “right” answer. He assigns the number 1 to a male child, and 0 to a female child. With the help of these symbols we can record eight three-digit permutations that describe all the possible situations for the three-child family:
Ω
= {000, 100, 010, 001, 110, 101, 011, 111},
where for example 011 indicates that the first child was a girl, followed by two boys. The article continues along the formal lines we described in section 41. We will use the symbol
A
for the event in which “the family has exactly one son,” and the symbol
B
for the situation in which “the family has at least two girls.” We must calculate the conditional probability
P
(
B
│
A
), which is . This is a fairly simple calculation. The article gives two methods, which give the same result. We will give the shorter one here: as it is known that there are two girls in the family, the relevant event, so claims the author, consists of four out of the eight possibilities listed above, and they are {000, 100, 010, 001}. In three of these there is a son in addition to the two daughters, so that the probability is
. This is a fairly simple calculation. The article gives two methods, which give the same result. We will give the shorter one here: as it is known that there are two girls in the family, the relevant event, so claims the author, consists of four out of the eight possibilities listed above, and they are {000, 100, 010, 001}. In three of these there is a son in addition to the two daughters, so that the probability is .
.
The article then addresses the second part of the question. It would seem, he warns, that in light of the above result, we would expect the probability to be as well. That is not correct (according to the article). Note: we know that the question relates to the child born last, so that the range of possibilities is just {001, 000}, and the probability is now
as well. That is not correct (according to the article). Note: we know that the question relates to the child born last, so that the range of possibilities is just {001, 000}, and the probability is now , and not
, and not . As stated above, the writer considers this a surprising result, or a paradox, which mathematics clarifies.
. As stated above, the writer considers this a surprising result, or a paradox, which mathematics clarifies.