Setting Foot on the Shores of Connemara (11 page)
Read Setting Foot on the Shores of Connemara Online
Authors: Tim Robinson
The difficulty of the concept of fractional dimensions is that our everyday idea of a dimension is a possible direction of
movement
. Thus within the space of a box, we can move an object from side to side, from front to back, and from top to bottom, that is, in
three independent dimensions. If the object is to be kept on a
tabletop
, a plane surface, it can only be moved from left to right, say, or from front to back – two
independent
dimensions; and if it is strung like a bead on a wire we can only slide it to and fro along that line of one dimension. There is no
generalizing
that idea to cover fractional dimensions; one cannot have two and a half directions. But there are other ways of conceiving of
dimensionality
, some of which can be stretched to cover fractals more comfortably. To get a taste of one of these, first note that some ordinary geometrical forms are, in a way, self-similar too. For instance a cube can be divided up into smaller cubes, each of which is similar to the whole but reduced by a certain factor, and then the smaller cubes can be dissected in the same way. Think of a cube with sides of unit length, divided up into little cubes with sides of length 1/
b
. (Fig. 4 shows the case where
b
= 4.) The number of little cubes fitting along one side of the big one is
b,
and the total number
N
of little cubes making up the big one is
b
x
b
x
b.
That is,
N
=
b
3
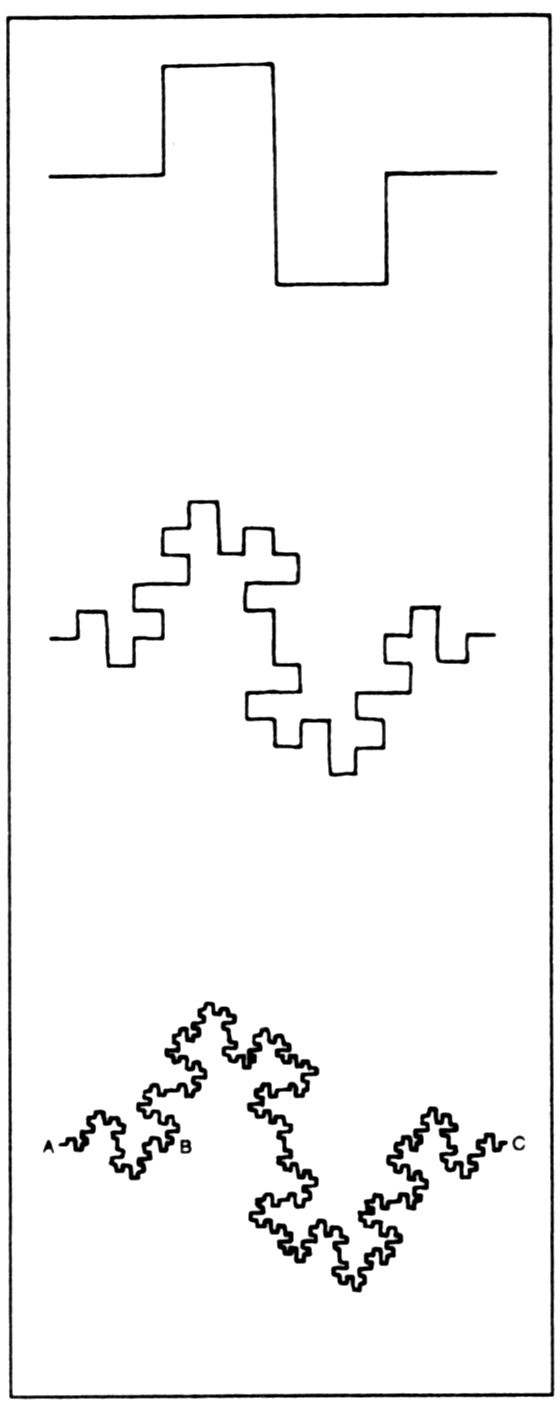
3. The first three stages in
constructing
a simple fractal; each stage is derived from the
preceding
one by replacing every straight bit by a reduced replica of the first stage.
Now think of a square with unit sides, divided up into smaller squares, each of which is the same as the big one but with its sides reduced by the factor 1
/b.
The number N of such small squares in the big one is given by
N
=
b
2
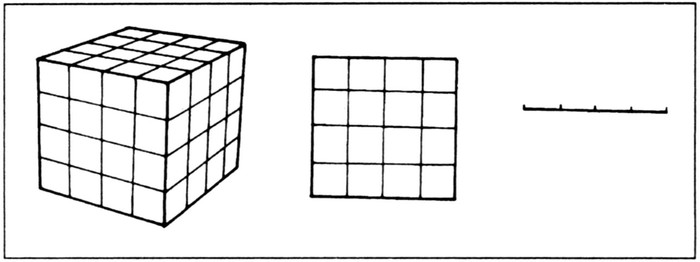
4. The self-similar dissection of a cube, a square, and a line.
And finally think of a line of unit length divided up into smaller sections of length 1/
b
; the number of them in the whole line is
N
=
b
In each case,
N
=
b
D
,
where the values of
D
agree with our idea that the cube has three dimensions, the square two, and the line one. Suppose though we take this equation as
defining
what is meant by dimensionality, and ask what result it gives when applied to a fractal form. The simplest case is the jigged form described above, of which any part, however tiny, will look roughly like the last curve in Fig. 3 when suitably magnified. The section of it from A to B, say, is made up of a number of parts such as that from A to C. Each of these parts is similar to the whole section but is smaller by a factor of 1/4; thus in analogy with the cube, the square and the line, in this case we have
b
= 4. And there are eight of them making up the whole, so
N
= 8. Putting these values into the equation N =
b
D
,
we have:
This way of looking at the idea of dimensions thus concurs with our normal ideas about simple shapes like squares arid cubes, and gives a result for fractals too; in this case it seems very well to express the feeling that there is more space in the ‘jigged line’ than there is in an ordinary one-dimensional line, but that it is still
something less than an area with two dimensions. One can easily construct examples which have a dimensionality of less than one, or between two and three. And the idea can be extended to cover irregular natural forms like coastlines and clouds, though here the results will be approximations, arrived at by statistical methods. Coastlines typically have dimensionalities of about 1.2; my very crude estimate for an average stretch of the south Connemara shore is 1.25, and the more complicated bits of it would give a higher answer still.
The fact that coastlines are virtually infinitely long had been stated before Mandelbrot, just as the concept of non-integral dimensionality had been suggested by earlier mathematicians; but it is Mandelbrot’s collation of the two ideas that opens onto new vistas of thought. A previously obscure topic in mathematics is suddenly important in physics, the earth sciences, biology and astrophysics, is crucial to the new disciplines of chaos and
complexity
theory, and promises to be a rich source of metaphor and imagery in literature and art. Like all discoveries it surprises us yet again with the unfathomable depth and texture of the natural world; specifically it shows that there is more space, there are more places, on a seashore, within a forest or among the galaxies, than the geometry of common sense allows.
The hints about the subject I gleaned from the newspaper cutting prompted me to get Mandelbrot’s book,
The
Fractal
Geo
metry
of
Nature.
2
It is an unlovely work in some ways (though without the abominable faults of the other principal sourcebook on the subject,
The
Beauty
of
Fractals
‚
3
which misidentifies the beauty of science and that of art, and crosses them to produce a hybrid with the virtues of neither). However, Mandelbrot’s concern with assessing his own priority in the field does lead him to discuss his intellectual forebears, and I was intrigued to learn that the
particular
concept of dimensionality he used (and of which I have given a very crude version above) was ‘formulated in Hausdorff 1919 and put in final form by Besicovitch’; in fact his mention of the latter name led me into the fractals of personal memory, which
eventually
spelt out a reason for my obsessive tracings of the Connemara shoreline. The anecdote involves another mathematical
construction
, the Peano Curve; so I had better clear the ground by
introducing
this old friend first.
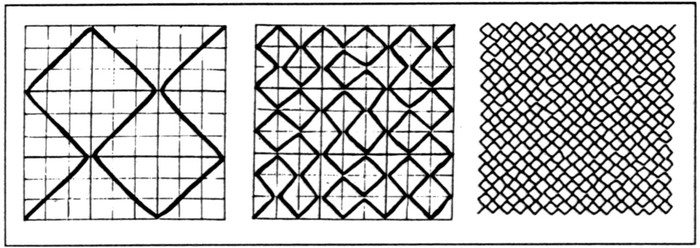
5. The first three stages in constructing a Peano Curve; each stage is derived from the preceding one by replacing every straight section by a reduced replica of the first stage.
We start with a line that zigzags through a square area (Fig. 5). First we replace each leg of it by a zigzag similar to, but smaller than, the first, and then do the same with each leg of the resultant more complex form, and so on, to the infinitely small. My diagram is crude, but drawing even the third stage is a maddening task and the fourth would be quite beyond my powers of attention. Of course the ultimate outcome is impossible to draw, because of the thickness of penpoints and the finiteness of human existence; it is a mathematical concept, like the perfect circle. Peano showed that such a curve actually visits every point within the square. In fact, while a line, however complicated, has a dimensionality of one, this object has the same dimensionality as the square, an area,
i.e.
two. Each little bit of it is a labyrinth in which each detour is a smaller labyrinth, in which each detour is a yet smaller labyrinth, and so on, beyond the dreams of Borges. At the time it was
discovered
– or created, according to one’s view of the nature of mathemetical objects – by the Italian mathematician Peano around the turn of the century, it was regarded as a geometrical
monstrosity
, an exception best disregarded in the name of logical hygiene.
I will nose briefly into just two of the labyrinthine digressions this diagram suggests, in the Irish context, before taking up my story. First: ‘How Celtic!’ Perhaps one could claim that fractal geometry is to Celtic art as Euclid is to classical art. While the mainstream of European culture has pursued its magnificent course, some other perception has been kept in mind by the Celtic periphery, all the way from La Tène Iron-Age curlicues to Jim Fitzpatrick’s kitsch-Celt goddesses. In a word, that a fascinating sort of beauty arises out of the repetitive interweaving of simple
elements. The beauty of Nature is often of this sort. In
Connemara
, which is pre-eminently the land of ‘dappled things’ –
drizzling
skies, bubbly streams, tussocky hillsides – one recognizes this texture. Of course, after a thorough soaking in all this dappled Celtic bewilderment, one runs for shelter in classical temples, with relief. And secondly: ‘How Ruskin would have liked this!’ In his book
Modern
Painters
, which is largely about how Turner achieved his version of truth to Nature, Ruskin devotes pages to analyzing such visual phenomena as a mackerel sky or the successive patterns of striations revealed on the peak of Mont Blanc as the sun moves round it. But cloud formations and geological fault systems are often fractal phenomena, and, lacking this concept, Ruskin’s numerical estimates of the number of dabs of cloud that go to make up the unified spectacle of a sunset sky are heroic but doomed attempts to render the beauty of the dappled things that classical art ignored, that it defined itself by excluding.
To return to my personal entanglement in the Peano Curve. Like various other apparently freakish inventions of turn-of-
the-century
mathematics, it was one of the hobby-horses of
Besicovitch
, who was an elderly and semi-retired professor of
mathematics
at Cambridge at the time I passed unremarkably through the place in the fifties. Mere crotchets on the spires of intellection; so Professor Besicovitch’s chosen topics appeared to me, a gauche would-be aesthete and week-old undergraduate, in the autumn of 1952. His best-known work was a treatise on
Almost Periodic Functions,
which sounded like a parody of professorial abstruosity. Besicovitch was to give an exceptional and to some degree
extra-curricular
series of seminars to the new intake. In the first of these, the professor, who had very little English other than
mathematical
terminology, outlined a number of his favourite problems, some of which still lacked solutions. An example: a line one inch long can obviously be turned around inside a circle one inch across, but what is the smallest area in which it can be turned around? It had long been accepted that the answer to this curious query was the area swept out by the line in making a three-point turn, a sort of concave-sided triangle. But the professor had demonstrated that in fact it can be turned around inside a shape of no area whatsoever, provided it is allowed to back off to infinity in an infinite number of different directions. A typical Besicovitch result; both ludicrous and mysterious. The image of that line’s
minnow-like dartings in all possible directions still remains with me as an emblem of a certain style of thought, and I suspect it also helped me fail my driving test. Having introduced us to
half-a-dozen
such bizarreries, the professor suggested that some of us might like to divide these problems between us, study them further, and lecture on them to the rest of the group. The first problem on offer concerned a way of representing a Peano Curve by a formula, an infinitely long and curiously constructed series of powers of a complex variable. It was, said Besicovitch, a very beautiful solution. Then he looked off into space rather sadly, and admitted that the curve this formula generated did pass through some points outside the square; nevertheless, it was a very fine solution. Also, he confessed, apparently quite disconsolate, it did pass through some points of the square more than once. But, taken all in all, it was a very beautiful solution. The proof was long, though, so he would suggest two of us divide it between us, to study it and report back to the group. Who would volunteer? He looked at us expectantly
en
masse
, and then, as no one responded, he appealed to us mutely, face by face. I had already glanced round the crowded lecture hall at my hundred or more unknown colleagues and decided they were a dull lot; I would have
preferred
to consort with the lovely and witty beings reading one of the arts subjects; but then for me the only point of art was to practise it, and I was convinced that all pedagogy stultified
creativity
, whereas I knew I could not climb the cliff-face of mathematics without help, and so had condemned myself to sojourn among these dullards. I recognized, all the same, that most of them had more mathematics than I, for I came from an unassuming
provincial
grammar school which had not previously aspired to prepare a pupil for Cambridge. But when Besicovitch said ‘Please!’, in tones of pain and embarrassment, I put up my hand out of impatience with the lot of them. To my relief someone I knew to be better educated than myself in such matters followed me into the breach.