Supercontinent: Ten Billion Years in the Life of Our Planet (24 page)
Read Supercontinent: Ten Billion Years in the Life of Our Planet Online
Authors: Ted Nield
If a large enough sample of true ages is gathered from ophiolites preserved during the formation of Pannotia, they should fall in a period entirely before the date of Rodinia’s break-up because the ocean floor they represent was all exterior to that supercontinent. Conversely, if the same is done for oceans that formed between the break-up of Pannotia and the formation of Pangaea, the ages obtained should fall within that interval of time because all the ocean floor they represent formed as an interior ocean. If these predictions hold up, our method should show that Rodinia extroverted to form Pannotia and Pannotia introverted to form Pangaea.
Geologists Professor Brendan Murphy of the Tectonics Research Laboratory at St Francis Xavier University, Nova Scotia, and Professor R. Damian Nance of Ohio University have pursued this technique with great success. Their elegant joint research has, since 1985, resulted in a much clearer picture of how supercontinents assemble. Murphy and Nance have looked at rocks associated with the assembly of Pannotia (about 600 million years old) from the Borborema Belt of Brazil, and the Trans-Saharan and Mozambique Belts of North and East Africa. Rodinia began to split apart about 760 million years ago. So, if Pannotia formed by the consumption of exterior ocean surrounding Rodinia, the formation dates should come out at between 760 million years and about 1100 million years.
But I still haven’t answered the main question: just how, exactly, do you find out such dates reliably? Simple radiometric dating, as we have already seen, allows you to find out when the atomic clock was last reset. But rocks from the floors of vanished oceans, now
anomalously
preserved in the mountain belts that replaced those oceans when they closed, have all been involved in mountain building and had their clocks reset. Simple radiometric dating would reveal the date the mountains formed, but that is not what we want. We want to get at the time these ocean floors formed at a mid-ocean ridge. We want the birthday, not the date of the funeral, or the mid-life facelift. We want to know the very first time those ocean-crust rocks were created by volcanic melts, erupting at a mid-ocean ridge; the very moment they were derived from the mantle and became part of the crust.
To find out that crucial birth-time, Murphy and Nance have
developed
a method that combines radiometric-dating techniques with the tendency of isotopes of elements to separate out: become differentiated during natural processes because of their different atomic weights. The technique is complex and beautiful, and it involves using isotopes of two unusual elements: samarium and its daughter element neodymium.
These two elements are very similar in many ways. Both sit close together in Group 3 of the Periodic Table, which occupies two long lines at the bottom of the chart, and which are collectively known as the ‘rare Earth elements’. On the top row (the ‘Lanthanide series’) you will find neodymium (Nd) at number 60 and samarium (Sm) at number 62. The atoms of these two elements are about the same size, and they react similarly in chemical processes because in their cloud of electrons both elements have the same number available for forming bonds – two. However, something different happens to neodymium and samarium atoms when rocks in the Earth’s mantle begin to melt and form the magma that will eventually build the ocean floor.
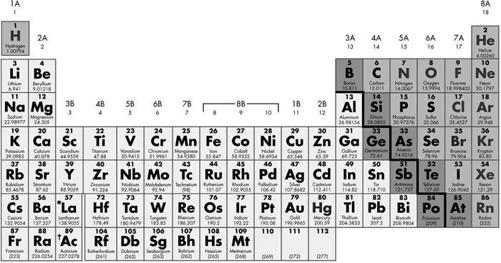

The Periodic Table of the Elements. The Lanthanide Series is one of the so-called ‘transition element’ groups (horizontal lines) arranged in a double line below the main diagram.
Lanthanide-series elements display a very strange property. As their atomic number (and hence their atomic weight) rises, the atoms actually
shrink
rather than expand. This is known as the Lanthanide contraction. When melting begins, rock becomes a mixture of liquid and solid. Lanthanide contraction makes the heavier and denser Lanthanides (such as samarium) more likely to stay where they are in the solid phase, while the lighter, bigger atoms such as neodymium will tend to prefer to melt. This means that neodymium atoms have a higher tendency to leave the mantle, and samarium to stay put. Mantle rocks have therefore become progressively depleted in neodymium since the planet formed 4700 million years ago.
If you could count all the atoms of samarium in the Earth and divide that number by the number of atoms of neodymium, you would get a figure that expressed their relative global abundance. If
the two elements were present in equal amounts, the number would, of course, be one. If you found more neodymium than samarium, then the resulting number would go down. For example, if there were twice as much neodymium as samarium, you would be dividing two into one, and the result would be 0.5. These numbers are called ratios, and they are useful in expressing the relative abundance of two things.
If you do the calculation for real, taking the Earth as a whole and dividing the number of Nd atoms into the number of Sm atoms, it works out at about 0.32: the ‘bulk Earth’ ratio. Or, putting it another way, there are about a third as many samarium atoms as neodymium atoms inside planet Earth.
But because, through geological time, Nd has been continually
leaving
the mantle in volcanic melts that have gone to form oceanic crust, Nd is more concentrated in the crust than in the Earth as a whole, so the samarium-to-neodymium (Sm/Nd) ratio of crustal rocks is lower, at 0.2. Conversely, Nd has been depleted from the mantle, so the mantle now contains less than average amounts of that element, making the Sm/Nd ratio of ‘depleted mantle’ higher (about 0.5, in fact).
So far we have not considered the matter of different
isotopes
of samarium and neodymium, but have thought of all the
isotopes
of each element collectively. However, both samarium and neodymium have isotopes aplenty. Samarium has seven natural ones, one of which, samarium-147, is unstable and undergoes radioactive decay to neodymium-143. This radioactive transformation is very slow indeed, with a half-life of 106 billion years – or over seven times the age of the universe. Neodymium has nine isotopes, seven of which are stable. One of them, neodymium-144, is not a product of any radioactive decay series, so it does not change in concentration in a given rock with time and therefore can be used as a benchmark.
The gradual decay of samarium-147 (
147
Sm) to neodymium-143 (
143
Nd) therefore has the effect of making
143
Nd more common
through geological time in all rocks, gradually increasing the ‘bulk Earth’ ratio between its daughter element
143
Nd and the unchanging
144
Nd. However, remember that there is more samarium in the depleted mantle than in the crust because of neodymium’s tendency to fractionate into melts that head upwards. Therefore the increase through time in the ratio of the two isotopes of neodymium will be faster in the depleted mantle (where the parent element samarium is relatively abundant) and slower in the crust, where Sm is rarer.
This means that the isotopic signature provided by the ratio of
143
Nd to
144
Nd gives the rock a fingerprint for its place of origin. Because radioactive decay processes are known, unchanging and
predictable
, you can then, by extrapolating backward, determine when the rock from which you obtained the sample left the mantle. It is as though the rock has never lost its accent: you can take the melt out of the mantle, but you can’t take the mantle out of the melt. Moreover, because samarium and neodymium are almost identical chemically, this fingerprint is almost indelible: it is almost unaffected by most subsequent changes that a rock might undergo.
This allows geologists to take more or less any rock that formed by the crystallization of magma – even if it formed by the remobilization of previous crustal rocks – and work out when its chemistry began to go its own way and depart from the isotope chemistry of the depleted mantle. This works because, in the end, nearly
all
rocks were originally derived from the upper mantle. As long as there has not been
contamination
from other melts with different histories (and this is usually evident from the field geology) the method is a sound way of telling when the rocks were first born.
This crucial date, the rock’s first birthday, is called the Depleted Mantle Model Age, abbreviated as
T
DM
. This is the tool we have been looking for: a way of telling when these pieces of ocean floor, now preserved in mountain belts, first left the mantle at a mid-ocean ridge.
Back now to the rocks. By taking as many samples as possible from ophiolite suite rocks that were emplaced during the elimination of the ocean we are studying, and then comparing their
T
DM
ages with the date that the mountain range formed (which we know independently from straightforward radiometric dating of that event), we should at last be able to determine whether that process was one of extroversion or introversion.
Using this technique, Murphy and Nance found that the rocks from Brazil that were caught up in the formation of Pannotia after what would become West Gondwana rifted off the previous supercontinent Rodinia, provide
T
DM
ages of about 1200 million years, and that
similar
rocks from south-west Algeria and southern Morocco come out at between 1200 and 950 million years. In the Mozambique Belt the
T
DM
ages come out at between 800 and 900 million years. From this they concluded that the vanished ocean, whose tombstone is those ancient mountain belts, formed part of Rodinia’s exterior ocean, because the
T
DM
ages are all older than the date of the break-up of Rodinia. As predicted by the Paul Hoffman model, Pannotia formed by the
extroversion
of Rodinia. Rodinia turned inside out.
In the case of Pangaea, the supercontinent after Pannotia, the results have been, as expected, very different, but also consistent with predictions. The main mountain ranges that formed as Pangaea reached its maximum packing – the great suture scars that mark the healing up of oceans – are the Appalachians in the USA, the Caledonian mountains of the UK and Norway, the Variscan
mountains
of southern Europe and the Urals of Russia. We know that Pangaea’s predecessor Pannotia began to fragment at about 550
million
years, when oceans like Iapetus began to form. So, as oceanic rocks caught up in the formation of Pangaea by the destruction of those ‘interior’ oceans, they should all have
T
DM
ages of less than 550 million years. No data are available as yet from the Urals, but data
from the other mountain belts all indicate that they were derived from the Earth’s mantle less than 550 million years ago. Pangaea formed by the accordion tectonics of introversion.
So, even from times 1000 million years in the past, geologists now are finding ways of determining how continental fragments moved about the face of the planet, consuming the ocean before them as they went. But this stately dance of the continents, which, like partners in a quadrille, move apart, twist around one another and come together again in new combinations, has not gone on for ever. Geologists can recognize the probable existence of even older supercontinents than Rodinia, though they will remain even more dubious and
controversial
until new techniques can be found to recover more information from the geological record.
But what makes ancient secrets more difficult still to unlock is the probability that in Earth’s deepest past the tectonic processes that operated were quite different from those we see around us today. For these distant pasts, the present no longer provides the key. The Earth may then have worked in ways perhaps as different from the
tectonics
of today as the Ediacara garden’s inhabitants may have been from modern life forms. And when it comes to life on Earth, geologists tracing the evolution of the planet from its Hadean origins are increasingly wondering how biology itself may owe both its
beginning
, and its drive to complexity, to the workings of our planet’s inner life – as told in the greatest palimpsest of all.