The Information (16 page)
The Difference Engine would run this process in reverse: instead of repeated subtraction to find the differences, it would generate sequences
of numbers by a cascade of additions. To accomplish this, Babbage conceived a system of figure wheels, marked with the numerals 0 to 9, placed along an axis to represent the decimal digits of a number: the units, the tens, the hundreds, and so on. The wheels would have gears. The gears along each axis would mesh with the gears of the next, to add the successive digits. As the machinery transmitted motion, wheel to wheel, it would be transmitting information, in tiny increments, the numbers summing across the axes. A mechanical complication arose, of course, when any sum passed 9. Then a unit had to be carried to the next decimal place. To manage this, Babbage placed a projecting tooth on each wheel, between the 9 and 0. The tooth would push a lever, which would in turn transmit its motion to the next wheel above.
At this point in the history of computing machinery, a new theme appears: the obsession with time. It occurred to Babbage that his machine had to compute faster than the human mind and as fast as possible. He had an idea for parallel processing: number wheels arrayed along an axis could add a row of the digits all at once. “If this could be accomplished,” he noted, “it would render additions and subtractions with numbers
having ten, twenty, fifty, or any number of figures, as rapid as those operations are with single figures.”
♦
He could see a problem, however. The digits of a single addition could not be managed with complete independence because of the carrying. The carries could overflow and cascade through a whole set of wheels. If the carries were known in advance, then the additions could proceed in parallel. But that knowledge did not become available in timely fashion. “Unfortunately,” he wrote, “there are multitudes of cases in which the carriages that become due are only known in successive periods of time.” He counted up the time, assuming one second per operation: to add two fifty-digit numbers might take only nine seconds in itself, but the carrying, in the worst case, could require fifty seconds more. Bad news indeed. “Multitudes of contrivances were designed, and almost endless drawings made, for the purpose of economizing the time,” Babbage wrote ruefully. By 1820 he had settled on a design. He acquired his own lathe, used it himself and hired metalworkers, and in 1822 managed to present the Royal Society with a small working model, gleaming and futuristic.
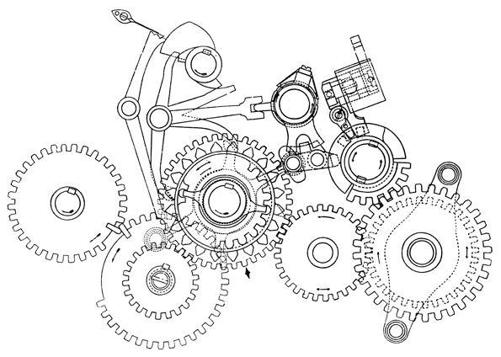
BABBAGE’S WHEEL-WORK
He was living in London near the Regent’s Park as a sort of gentleman philosopher, publishing mathematical papers and occasionally lecturing to the public on astronomy. He married a wealthy young woman from Shropshire, Georgiana Whitmore, the youngest of eight sisters. Beyond what money she had, he was supported mainly by a £300 allowance from his father—whom he resented as a tyrannical, ungenerous, and above all close-minded old man. “It is scarcely too much to assert that he
believes
nothing he
hears
, and only half of what he sees,”
♦
Babbage wrote his friend Herschel. When his father died, in 1827, Babbage inherited a fortune of £100,000. He briefly became an actuary for a new Protector Life Assurance Company and computed statistical tables rationalizing life expectancies. He tried to get a university professorship, so far unsuccessfully, but he had an increasingly lively social life, and in scholarly circles people were beginning to know his name. With Herschel’s help he was elected a fellow of the Royal Society.
Even his misfires kindled his reputation. On behalf of
The Edinburgh Journal of Science
Sir David Brewster sent him a classic in the annals of rejection letters: “It is with no inconsiderable degree of reluctance that I decline the offer of any Paper from you. I think, however, you will upon reconsideration of the subject be of opinion that I have no other alternative. The subjects you propose for a series of Mathematical and Metaphysical Essays are so very profound, that there is perhaps not a single subscriber to our Journal who could follow them.”
♦
On behalf of his nascent invention, Babbage began a campaign of demonstrations and letters. By 1823 the Treasury and the Exchequer had grown interested. He promised them “logarithmic tables as cheap as potatoes”
♦
—how could they resist? Logarithms saved ships. The Lords of the Treasury authorized a first appropriation of £1,500.
As an abstract conception the Difference Engine generated excitement that did not need to wait for anything so mundane as the machine’s actual construction. The idea was landing in fertile soil. Dionysius Lardner, a popular lecturer on technical subjects, devoted a series of public talks to Babbage, hailing his “proposition to reduce arithmetic to the dominion of mechanism,—to substitute an automaton for a compositor,—to throw the powers of thought into wheel-work.”
♦
The engine “must, when completed,” he said, “produce important effects, not only on the progress of science, but on that of civilization.” It would be the
rational
machine. It would be a junction point for two roads—mechanism and thought. Its admirers sometimes struggled with their explanations of this intersection: “The question is set to the instrument,” Henry Colebrooke told the Astronomical Society, “or the instrument is set to the question.”
♦
Either way, he said, “by simply giving motion the solution is wrought.”
But the engine made slower progress in the realm of brass and wrought iron. Babbage tore out the stables in back of his London house and replaced them with a forge, foundry, and fireproofed workshop. He
engaged Joseph Clement, a draftsman and inventor, self-educated, the son of a village weaver who had made himself into England’s preeminent mechanical engineer. Babbage and Clement realized that they would have to make new tools. Inside a colossal iron frame the design called for the most intricate and precise parts—axles, gears, springs, and pins, and above all figure wheels by the hundreds and then thousands. Hand tools could never produce the components with the needed precision. Before Babbage could have a manufactory of number tables, he would have to build new manufactories of parts. The rest of the Industrial Revolution, too, needed standardization in its parts: interchangeable screws of uniform thread count and pitch; screws as fundamental units. The lathes of Clement and his journeymen began to produce them.
As the difficulties grew, so did Babbage’s ambitions. After ten years, the engine stood twenty-four inches high, with six vertical axles and dozens of wheels, capable of computing six-figure results. Ten years after that, the scale—on paper—had reached 160 cubic feet, 15 tons, and 25,000 parts, and the paper had spread, too, the drawings covering more than 400 square feet. The level of complexity was confounding. Babbage solved the problem of adding many digits at once by separating the “adding motions” from the “carrying motions” and then staggering the timing of the carries. The addition would begin with a rush of grinding gears, first the odd-numbered columns of dials, then the even columns. Then the carries would recoil across the rows. To keep the motion synchronized, parts of the machine would need to “know” at critical times that a carry was pending. The information was conveyed by the state of a latch. For the first time, but not the last, a device was invested with memory. “It is in effect a memorandum taken by the machine,” wrote his publicizer, Dionysius Lardner. Babbage himself was self-conscious about anthropomorphizing but could not resist. “The mechanical means I employed to make these carriages,” he suggested, “bears some slight analogy to the operation of the faculty of memory.”
In ordinary language, to describe even this basic process of addition required a great effulgence of words, naming the metal parts, accounting for their interactions, and sorting out interdependencies that multiplied to form a long chain of causality. Lardner’s own explanation of “carrying,” for example, was epic.
♦
A single isolated instant of the action involved a dial, an index, a thumb, an axis, a trigger, a notch, a hook, a claw, a spring, a tooth, and a ratchet wheel:
Now, at the moment that the division between 9 and 0 on the dial B
2
passes under the index, a thumb placed on the axis of this dial touches a trigger which raises out of the notch of the hook which sustains the claw just mentioned, and allows it to fall back by the recoil of the spring, and drop into the next tooth of the ratchet wheel.
Hundreds of words later, summing up, Lardner resorted to a metaphor suggesting fluid dynamics:
There are two systems of waves of mechanical action continually flowing from the bottom to the top; and two streams of similar action constantly passing from the right to the left. The crests of the first system of adding waves fall upon the last difference, and upon every alternate one proceeding upwards.… The first stream of carrying action passes from right to left along the highest row and every alternate row.
This was one way of abstracting from the particular—the particulars being so intricate. And then he surrendered. “Its wonders, however, are still greater in its details,” he wrote. “We despair of doing it justice.”
Nor were ordinary draftsman’s plans sufficient for describing this machine that was more than a machine. It was a dynamical system, its many parts each capable of several modes or states, sometimes at rest and sometimes in motion, propagating their influence along convoluted channels. Could it ever be specified completely, on paper? Babbage, for his own purposes, devised a new formal tool, a system of “mechanical notation” (his term). This was a language of signs meant to represent not just the physical form of a machine but its more elusive properties: its timing and its logic. It was an extraordinary ambition, as Babbage himself appreciated. In 1826 he proudly reported to the Royal Society “On a Method of Expressing by Signs the Action of Machinery.”
♦
In part it was an exercise in classification. He analyzed the different ways in which something—motion, or power—could be “communicated” through a system. There were many ways. A part could receive its influence simply by being attached to another part, “as a pin on a wheel, or a wheel and pinion on the same axis.” Or transmission could occur “by stiff friction.” A part might be driven constantly by another part “as happens when a wheel is driven by a pinion”—or
not
constantly, “as is the case when a stud lifts a bolt once in the course of a revolution.” Here a vision of logical branching entered the scheme: the path of communication would vary depending on the alternative states of some part of the machine.
Babbage’s mechanical notation followed naturally from his work on symbolic notation in mathematical analysis. Machinery, like mathematics, needed rigor and definition for progress. “The forms of ordinary language were far too diffuse,” he wrote. “The signs, if they have been properly chosen, and if they should be generally adopted, will form as it were an universal language.” Language was never a side issue for Babbage.
He finally won a university post, at Cambridge: the prestigious Lucasian Professorship of Mathematics, formerly occupied by Newton. As in Newton’s time, the work was not onerous. Babbage did not have to teach students, deliver lectures, or even live in Cambridge, and this was just as well, because he was also becoming a popular fixture of London social life. At home at One Dorset Street he hosted a regular Saturday soirée that drew a glittering crowd—politicians, artists, dukes and duchesses, and the greatest English scientists of the age: Charles Darwin, Michael Faraday, and Charles Lyell, among others.
♦
They marveled at his calculating machine and, on display nearby, the dancing automaton of his youth. (In invitations he would write, “I hope you intend to patronise the ‘Silver Lady.’ She is to appear in new dresses and decorations.”) He was a mathematical raconteur—that was no contradiction, in this time and place. Lyell reported approvingly that he “jokes and reasons in high mathematics.” He published a much-quoted treatise applying probability theory to the theological question of miracles. With tongue in cheek he wrote Alfred, Lord Tennyson, to suggest a correction for the poet’s couplet: “Every minute dies a man, / Every minute one is born.”
