The Rational Animal: How Evolution Made Us Smarter Than We Think (18 page)

The Wason card problem is difficult for most people, in the same way that learning to write is difficult.
Unless you took advanced conditional reasoning in college, it’s not that easy to derive the right answer—it’s like asking an illiterate person to write an essay.
Even philosophy professors and mathematicians tend to get the answer wrong (in fact, we wrote the wrong answer when writing this book and had to go back and correct it two separate times).

But what if there were a way to make this problem less like doing ballet and more like walking?
Leda Cosmides, an evolutionary psychologist at the University of California, Santa Barbara, has figured out how to do just that.
Although solving abstract logic problems is evolutionarily novel and therefore difficult, Cosmides suspected that humans have been solving all sorts of complex logical problems for hundreds of thousands of years.
As it turns out, solving one of those ancestral problems requires the same exact complex logic as solving the Wason card problem.

This ancestral problem is a specialty of our affiliation subself, which is a master manager of life in social groups.
Here’s why: Living in social groups brings many advantages.
With ten heads working on a problem, the odds of discovering a solution rise dramatically.
But anyone who has ever worked on a group project knows that there’s also a downside to working in groups—some people end up taking the credit without doing their part.
When our ancestors were living in small groups and facing frequent dangers of starvation, it was critical to figure out which people were taking more than they were giving.
Having a couple of group members who ate their share of the food but didn’t do their share of the hunting and gathering could mean the difference between starvation and survival.
Our ancestors needed to be good at detecting social parasites—the cheaters in our midst.

Leda Cosmides realized that the logical reasoning people use to detect cheaters involves the exact same logical reasoning needed to solve the Wason card problem.
Let’s revisit the card problem, except this time we’ll state the problem in a way that allows the affiliation subself to process this information in the way our ancestors did:

Figure 5.3
shows four cards. Each card has a person’s age on one side and the beverage he or she is drinking on the other. Which card(s) do you need to turn over in order to test whether the following rule is true: If a person is drinking alcohol, he or she must be over eighteen?

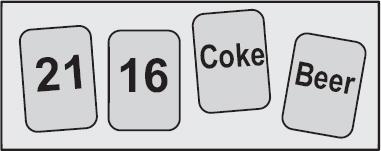
Figure 5.3.
The Cheater Detection version of the Wason Task

When presented with this translated version of the problem, most people instantly get the right answer: turn over the card with “16” and the card with “beer,” while leaving the other two cards unturned.
It’s pointless to turn over the card with “21” because we know that this person isn’t a cheater.
It’s similarly useless to turn over the card of the person who’s drinking a Coke because that person did not receive the benefit that could come from cheating.

The complex logic required to solve the cheater problem is mathematically identical to the complex logic needed to solve the Wason
card problem we gave you earlier.
Cosmides tried dozens of versions of the problem, always finding the same results.
Regardless of whether the question was about familiar things like the drinking age or unfamiliar things like the right to eat cassava roots, if the problem involved detecting a cheater, most people became brilliant logicians.

Larry Sugiyama, the anthropologist we met at the beginning of the chapter, had the Shiwiar try to solve this problem.
Whereas the Shiwiar solved the original Wason card task 0 percent of the time, they solved the evolutionarily translated version 83 percent of the time.
This was in fact one point better than Harvard students, so in an intellectual Olympics, the unschooled Shiwiar would have beat out the well-educated Cambridge team on the natural version of this problem.

Cosmides and Sugiyama demonstrated something extremely important.
It’s not the case that people are incapable of doing complex logic.
Instead, most academic problems are written in such a way that they never engage the sophisticated talents of our subselves.
It’s like asking a car mechanic to solve the problem of lifting a car not by using a jack but by demonstrating the answer in terms of mathematical vectors and energy exchange.

One of us just tried the cheater detection problem on our seven-year-old son, who has yet to be educated in multiplication, much less conditional probability.
He had a difficult time understanding the Wason card task, wanting to turn over every card.
But when the problem was framed in terms of people who either had or had not paid the fee to play a special Lego Universe computer game, he nailed the answer easily.
Whereas the original card task is tough, like writing an essay about family relations in the modern world, the evolutionarily translated version is like chatting with a neighbor about how your kids are doing.
Writing is hard, and talking is easy, even when you are attempting to communicate the same exact thing.

THE LARGE NUMBERS PARADOX

Imagine you learn that there was a plane crash, and all two hundred people aboard perished.
You wouldn’t be human if you didn’t feel
some sadness and grief in response to this news.
Now imagine instead that it was a larger plane, and the crash resulted in six hundred fatalities.
How would you feel?

Most people would again feel grief and sadness, but they wouldn’t feel three times as much grief and sadness.
In fact, people experience about the same level of emotion in both situations—and sometimes they experience less emotion when more people perish.

This is known as the
large numbers paradox
.
You can find it all around you.
Many Americans, for example, are outraged when they learn that the US military presence in Iraq and Afghanistan in the first decade of the twenty-first century cost taxpayers over $1 billion.
But those people wouldn’t feel much more outrage if they were told that the endeavor cost over $1 trillion—even though the latter amount is over a thousand times greater and, in fact, closer to the actual cost.
It’s mathematically equivalent to the difference between the clerk at the corner store charging you $4 versus $4,000 for the same sandwich.
Yet when government expenses are multiplied a thousand times, people don’t get any angrier!

To understand this paradox we need to navigate through the jungle back to the world of the Shiwiar.
The Shiwiar live in small villages of about fifty to one hundred people.
Each villager knows most of these people, many of whom are relatives or close friends.
The range of fifty to one hundred is important because it appears again and again around the globe and across time.
Modern hunter-gatherers, from Africa to South America to Oceania, live in bands of about fifty to one hundred people.
If you were the first explorer to contact a tribe of people who had never seen an outsider, smart money says you’d find about fifty to one hundred people in that tribe.
Archaeological evidence suggests that if you traveled back in time one hundred thousand years to visit your great, great, great .
.
.
great-grandmother, you’d likely find her living in a nomadic band of fifty to one hundred people.
Today many of us live in cities of millions.
Yet our social networks—the people we interact with—still include about fifty to one hundred people.

If you went up to a Shiwiar chief and told him that six hundred people might perish, he’d probably scratch his head and say, “Hunh?
What does this mean?”
Hunter-gatherer societies tend to have very few words for numbers and amounts.
You might find “one,” “two,” “a few,” “tribe size.”
Were we to start discoursing about 200, 600, 1 million, 1 billion, the Shiwiar’s eyes would likely glaze over (just as ours do at the distinction between a billion and a trillion).

Making reasoned decisions involving calculations with large numbers is an evolutionarily novel concept—it’s like writing, not talking.
While it’s perhaps amusing to think about how the Shiwiar might respond to large numbers, keep in mind that your brain is pretty much evolutionarily identical to a Shiwiar’s brain, which is in turn similar to the brains of the common ancestors of all human beings, who migrated out of Africa approximately fifty thousand years ago.
We are all modern cavemen.
Many of us have spent long years in math classes, and we cognitively comprehend that we need to add three zeros to turn a thousand into a million.
Yet, as the paradoxical plane crash and taxpayer examples illustrate, our brains get a bit numb when numbers get big.
What’s a light-year again, or what’s 10
¹²
nanometers?
To our brains, the very big number is a fuzzy concept devoid of evolutionary relevance.
This really matters if we want to understand people’s erroneous and irrational decisions.
Asking the average person to reason out logical questions laced with large numbers is a bit like asking him or her to perform
Swan Lake
at the Metropolitan Opera House.

ERASING ERRORS BY ENGAGING THE AFFILIATION SUBSELF

Daniel Kahneman and Amos Tversky make up the dynamic duo whose groundbreaking research in judgment and decision making garnered a Nobel Prize.
Among their many contributions to behavioral economics, they are known for devising a number of particularly clever questions to expose the fallibility of human reasoning.
One such question goes like this:

Imagine that the United States is preparing for the outbreak of an unusual Asian disease, which is expected to kill six hundred

people. Two alternative programs to combat the disease have been proposed.

Program A:
If Program A is adopted, two hundred people will be saved.

Program B:
If Program B is adopted, there is a one-third probability that six hundred people will be saved and a two-thirds probability that no people will be saved.

Which of the two programs would you favor?

The first thing to notice is that both options have the exact same “expected value” for the average number of people who are expected to remain alive—two hundred out of six hundred.
The difference between the two options is this: whereas Program A provides a precise number for how many people are going to be saved for certain, Program B is fraught with uncertainty.
Tversky and Kahneman found that the majority of people (72 percent) chose the more certain Program A.

But discovering that people like the more certain option didn’t win them the Nobel Prize.
The important twist is what happened next.
A second group of people were given the same Asian disease problem and provided with the same options.
But the options were framed just a little bit differently:

Program A:
If Program A is adopted, four hundred people will die.

Program B:
If Program B is adopted, there is a one-third probability that nobody will die, and a two-thirds probability that six hundred people will die.

Which of the two programs would you favor?

It’s critical to note that this second problem is logically and mathematically the exact same problem as the first one.
Again, both options have the same expected value for the average number of people who are expected to remain alive—two hundred out of six hundred.
The only difference is that the options are never framed as losses instead of gains.
However, when presented with the latter two options, the majority of people (78 percent) now chose the less certain option B.
This preference reversal seems to reveal a blatant miscalibration in decision making.

People’s fickle preference reversal in the Asian disease problem is often presented as a hallmark of human irrationality and a crushing blow to the central assumptions of the classical economic model of rational man.
It’s not that people are bad at math (the numbers in the problem are intentionally round so that all college students can easily calculate the expected values in their head).
Instead, people just seem irrationally inconsistent in dealing with mathematically identical decisions.

But before we close the case and conclude that educated individuals are mostly moronic decision makers, let’s do a little detective work with our evolutionary magnifying lens.
We know that our ancestors lived in bands of one hundred people or fewer.
And we know that our brains are not designed to comprehend large numbers.
Remember, our ancestors would not have encountered such quantities.

Decision scientist X.
T.
Wang suspected that the classic Asian disease problem might be an evolutionarily novel contraption that fails to tap our deeper ancestral logic.
Wang thought that the problem is like asking an illiterate person to write, or like asking Doug and Vlad to perform a few ballet movements from
Swan Lake
(take our word for it, you don’t want to see either of us in tights).