Thinking, Fast and Slow (32 page)
Read Thinking, Fast and Slow Online
Authors: Daniel Kahneman
You can measure the extent of your aversion to losses by asking yourself a question: What is the smallest gain that I need to balance an equal chance to lose $100? For many people the answer is about $200, twice as much as the loss. The “loss aversion ratio” has been estimated in several experiments and is usually in the range of 1.5 to 2.5. This is an average, of course; some people are much more loss averse than others. Professional risk takers in the financial markets are more tolerant of losses, probably because they do not respond emotionally to every fluctuation. When participants in an experiment were instructed to “think like a trader,” they became less loss averse and their emotional reaction to losses (measured by a physiological index of emotional arousal) was sharply reduced.
In order to examine your loss aversion ratio for different stakes, consider the following questions. Ignore any social considerations, do not try to appear either bold Blth"vioher or cautious, and focus only on the subjective impact of the possible loss and the off setting gain.
- Consider a 5 0–5 0 gamble in which you can lose $10. What is the smallest gain that makes the gamble attractive? If you say $10, then you are indifferent to risk. If you give a number less than $10, you seek risk. If your answer is above $10, you are loss averse.
- What about a possible loss of $500 on a coin toss? What possible gain do you require to off set it?
- What about a loss of $2,000?
As you carried out this exercise, you probably found that your loss aversion coefficient tends to increase when the stakes rise, but not dramatically. All bets are off, of course, if the possible loss is potentially ruinous, or if your lifestyle is threatened. The loss aversion coefficient is very large in such cases and may even be infinite—there are risks that you will not accept, regardless of how many millions you might stand to win if you are lucky.
Another look at figure 10 may help prevent a common confusion. In this chapter I have made two claims, which some readers may view as contradictory:
- In mixed gambles, where both a gain and a loss are possible, loss aversion causes extremely risk-averse choices.
- In bad choices, where a sure loss is compared to a larger loss that is merely probable, diminishing sensitivity causes risk seeking.
There is no contradiction. In the mixed case, the possible loss looms twice as large as the possible gain, as you can see by comparing the slopes of the value function for losses and gains. In the bad case, the bending of the value curve (diminishing sensitivity) causes risk seeking. The pain of losing $900 is more than 90% of the pain of losing $1,000. These two insights are the essence of prospect theory.
Figure 10 shows an abrupt change in the slope of the value function where gains turn into losses, because there is considerable loss aversion even when the amount at risk is minuscule relative to your wealth. Is it plausible that attitudes to states of wealth could explain the extreme aversion to small risks? It is a striking example of theory-induced blindness that this obvious flaw in Bernoulli’s theory failed to attract scholarly notice for more than 250 years. In 2000, the behavioral economist Matthew Rabin finally proved mathematically that attempts to explain loss aversion by the utility of wealth are absurd and doomed to fail, and his proof attracted attention. Rabin’s theorem shows that anyone who rejects a favorable gamble with small stakes is mathematically committed to a foolish level of risk aversion for some larger gamble. For example, he notes that most Humans reject the following gamble:
50% chance to lose $100 and 50% chance to win $200
He then shows that according to utility theory, an individual who rejects that gamble will also turn down the following gamble:
50% chance to lose $200 and 50% chance to win $20,000
But of course no one in his or her right mind will reject this gamble! In an exuberant article they wrote abo Blth"ins>
Perhaps carried away by their enthusiasm, they concluded their article by recalling the famous Monty Python sketch in which a frustrated customer attempts to return a dead parrot to a pet store. The customer uses a long series of phrases to describe the state of the bird, culminating in “this is an ex-parrot.” Rabin and Thaler went on to say that “it is time for economists to recognize that expected utility is an ex-hypothesis.” Many economists saw this flippant statement as little short of blasphemy. However, the theory-induced blindness of accepting the utility of wealth as an explanation of attitudes to small losses is a legitimate target for humorous comment.
Blind Spots pf Prospect Theory
So far in this part of the book I have extolled the virtues of prospect theory and criticized the rational model and expected utility theory. It is time for some balance.
Most graduate students in economics have heard about prospect theory and loss aversion, but you are unlikely to find these terms in the index of an introductory text in economics. I am sometimes pained by this omission, but in fact it is quite reasonable, because of the central role of rationality in basic economic theory. The standard concepts and results that undergraduates are taught are most easily explained by assuming that Econs do not make foolish mistakes. This assumption is truly necessary, and it would be undermined by introducing the Humans of prospect theory, whose evaluations of outcomes are unreasonably short-sighted.
There are good reasons for keeping prospect theory out of introductory texts. The basic concepts of economics are essential intellectual tools, which are not easy to grasp even with simplified and unrealistic assumptions about the nature of the economic agents who interact in markets. Raising questions about these assumptions even as they are introduced would be confusing, and perhaps demoralizing. It is reasonable to put priority on helping students acquire the basic tools of the discipline. Furthermore, the failure of rationality that is built into prospect theory is often irrelevant to the predictions of economic theory, which work out with great precision in some situations and provide good approximations in many others. In some contexts, however, the difference becomes significant: the Humans described by prospect theory are guided by the immediate emotional impact of gains and losses, not by long-term prospects of wealth and global utility.
I emphasized theory-induced blindness in my discussion of flaws in Bernoulli’s model that remained unquestioned for more than two centuries. But of course theory-induced blindness is not restricted to expected utility theory. Prospect theory has flaws of its own, and theory-induced blindness to these flaws has contributed to its acceptance as the main alternative to utility theory.
Consider the assumption of prospect theory, that the reference point, usually the status quo, has a value of zero. This assumption seems reasonable, but it leads to some absurd consequences. Have a good look at the following prospects. What would it be like to own them?
A. one chance in a million to win $1 million
B. 90% chance to win $12 and 10% chance to win nothing
C. 90% chance to win $1 million and 10% chance to win nothing
Winning nothing is a possible outcome in all three gambles, and prospect theory assigns the same value to that outcome in the three cases. Winning nothing is the reference point and its value is zero. Do these statements correspond to your experience? Of course not. Winning nothing is a nonevent in the first two cases, and assigning it a value of zero makes good sense. In contrast, failing to win in the third scenario is intensely disappointing. Like a salary increase that has been promised informally, the high probability of winning the large sum sets up a tentative new reference point. Relative to your expectations, winning nothing will be experienced as a large loss. Prospect theory cannot cope with this fact, because it does not allow the value of an outcome (in this case, winning nothing) to change when it is highly unlikely, or when the alternative is very valuable. In simple words, prospect theory cannot deal with disappointment. Disappointment and the anticipation of disappointment are real, however, and the failure to acknowledge them is as obvious a flow as the counterexamples that I invoked to criticize Bernoulli’s theory.
Prospect theory and utility theory also fail to allow for regret. The two theories share the assumption that available options in a choice are evaluated separately and independently, and that the option with the highest value is selected. This assumption is certainly wrong, as the following example shows.
Problem 6: Choose between 90% chance to win $1 million OR $50 with certainty.
Problem 7: Choose between 90% chance to win $1 million OR $150,000 with certainty.
Compare the anticipated pain of choosing the gamble and
not
winning in the two cases. Failing to win is a disappointment in both, but the potential pain is compounded in problem 7 by knowing that if you choose the gamble and lose you will regret the “greedy” decision you made by spurning a sure gift of $150,000. In regret, the experience of an outcome depends on an option you could have adopted but did not.
Several economists and psychologists have proposed models of decision making that are based on the emotions of regret and disappointment. It is fair to say that these models have had less
influence than prospect theory, and the reason is instructive. The emotions of regret and disappointment are real, and decision makers surely anticipate these emotions when making their choices. The problem is that regret theories make few striking predictions that would distinguish them from prospect theory, which has the advantage of being simpler. The complexity of prospect theory was more acceptable in the competition with expected utility theory because it did predict observations that expected utility theory could not explain.
Richer and more realistic assumptions do not suffice to make a theory successful. Scientists use theories as a bag of working tools, and they will not take on the burden of a heavier bag unless the new tools are very useful. Prospect theory was accepted by many scholars not because it is “true” but because the concepts that it added to utility theory, notably the reference point and loss aversion, were worth the trouble; they yielded new predictions that turned out to be true. We were lucky.
Speaking of Prospect Theory
“He suffers from extreme loss aversion, which makes him turn down very favorable opportunities.”
“Considering her vast wealth, her emotional response to trivial gains and losses makes no sense.”
“He weighs losses about twice as much as gains, which is normal.”
You have probably seen figure 11 or a close cousin of it even if you never had a class in economics. The graph displays an individual’s “indifference map” for two goods.
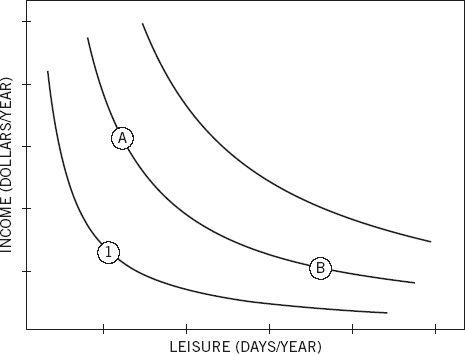
Figure 11
Students learn in introductory economics classes that each point on the map specifies a particular combination of income and vacation days. Each “indifference curve” connects the combinations of the two goods that are equally desirable—they have the same utility. The curves would turn into parallel straight lines if people were willing to “sell” vacation days for extra income at the same price regardless of how much income and how much vacation time they have. The convex shape indicates diminishing marginal utility: the more leisure you have, the less you care for an extra day of it, and each added day is worth less than the one before. Similarly, the more income you have, the less you care for an extra dollar, and the amount you are willing to give up for an extra day of leisure increases.
All locations on an indifference curve are equally attractive. This is literally what indifference means: you don’t care where you are on an indifference curve. So if A and B are on the same indifference curve for you, you are indifferent between them and will need no incentive to move from one to the other, or back. Some version of this figure has appeared in every economics textbook written in the last hundred years, and many millions of students have stared at it. Few have noticed what is missing. Here again, the power and elegance of a theoretical model have blinded students and scholars to a serious deficiency.
What is missing from the figure is an indication of the individual’s current income and leisure. If you are a salaried employee, the terms of your employment specify a salary and a number of vacation days, which is a point on the map. This is your reference point, your status quo, but the figure does not show it. By failing to display it, the theorists who draw this figure invite you to believe that the reference point does not matter, but by now you know that of course it does. This is Bernoulli’s error all over again. The representation of indifference curves implicitly assumes that your utility at any given moment is determined entirely by your present situation, that the past is irrelevant, and that your evaluation of a possible job does not depend on the terms of your current job. These assumptions are completely unrealistic in this case and in many others.
The omission of the ref Con serence point from the indifference map is a surprising case of theory-induced blindness, because we so often encounter cases in which the reference point obviously matters. In labor negotiations, it is well understood by both sides that the reference point is the existing contract and that the negotiations will focus on mutual demands for concessions relative to that reference point. The role of loss aversion in bargaining is also well understood: making concessions hurts. You have much personal experience of the role of reference point. If you changed jobs or locations, or even considered such a change, you surely remember that the features of the new place were coded as pluses or minuses relative to where you were. You may also have noticed that disadvantages loomed larger than advantages in this evaluation—loss aversion was at work. It is difficult to accept changes for the worse. For example, the minimal wage that unemployed workers would accept for new employment averages 90% of their previous wage, and it drops by less than 10% over a period of one year.
To appreciate the power that the reference point exerts on choices, consider Albert and Ben, “hedonic twins” who have identical tastes and currently hold identical starting jobs, with little income and little leisure time. Their current circumstances correspond to the point marked 1 in figure 11. The firm offers them two improved positions, A and B, and lets them decide who will get a raise of $10,000 (position A) and who will get an extra day of paid vacation each month (position B). As they are both indifferent, they toss a coin. Albert gets the raise, Ben gets the extra leisure. Some time passes as the twins get accustomed to their positions. Now the company suggests they may switch jobs if they wish.
The standard theory represented in the figure assumes that preferences are stable over time. Positions A and B are equally attractive for both twins and they will need little or no incentive to switch. In sharp contrast, prospect theory asserts that both twins will definitely prefer to remain as they are. This preference for the status quo is a consequence of loss aversion.
Let us focus on Albert. He was initially in position 1 on the graph, and from that reference point he found these two alternatives equally attractive:
Go to A: a raise of $10,000
OR
Go to B: 12 extra days of vacation
Taking position A changes Albert’s reference point, and when he considers switching to B, his choice has a new structure:
Stay at A: no gain and no loss
OR
Move to B: 12 extra days of vacation and a $10,000 salary cut
You just had the subjective experience of loss aversion. You could feel it: a salary cut of $10,000 is very bad news. Even if a gain of 12 vacation days was as impressive as a gain of $10,000, the same improvement of leisure is not sufficient to compensate for a loss of $10,000. Albert will stay at A because the disadvantage of moving outweighs the advantage. The same reasoning applies to Ben, who will also want to keep his present job because the loss of now-precious leisure outweighs the benefit of the extra income.
This example highlights two aspects of choice that the st Bon s Ae st Bonandard model of indifference curves does not predict. First, tastes are not fixed; they vary with the reference point. Second, the disadvantages of a change loom larger than its advantages, inducing a bias that favors the status quo. Of course, loss aversion does not imply that you never prefer to change your situation; the benefits of an opportunity may exceed even overweighted losses. Loss aversion implies only that choices are strongly biased in favor of the reference situation (and generally biased to favor small rather than large changes).
Conventional indifference maps and Bernoulli’s representation of outcomes as states of wealth share a mistaken assumption: that your utility for a state of affairs depends only on that state and is not affected by your history. Correcting that mistake has been one of the achievements of behavioral economics.
The Endowment Effect
The question of when an approach or a movement got its start is often difficult to answer, but the origin of what is now known as behavioral economics can be specified precisely. In the early 1970s, Richard Thaler, then a graduate student in the very conservative economics department of the University of Rochester, began having heretical thoughts. Thaler always had a sharp wit and an ironic bent, and as a student he amused himself by collecting observations of behavior that the model of rational economic behavior could not explain. He took special pleasure in evidence of economic irrationality among his professors, and he found one that was particularly striking.
Professor R (now revealed to be Richard Rosett, who went on to become the dean of the University of Chicago Graduate School of Business) was a firm believer in standard economic theory as well as a sophisticated wine lover. Thaler observed that Professor R was very reluctant to sell a bottle from his collection—even at the high price of $100 (in 1975 dollars!). Professor R bought wine at auctions, but would never pay more than $35 for a bottle of that quality. At prices between $35 and $100, he would neither buy nor sell. The large gap is inconsistent with economic theory, in which the professor is expected to have a single value for the bottle. If a particular bottle is worth $50 to him, then he should be willing to sell it for any amount in excess of $50. If he did not own the bottle, he should be willing to pay any amount up to $50 for it. The just-acceptable selling price and the just-acceptable buying price should have been identical, but in fact the minimum price to sell ($100) was much higher than the maximum buying price of $35. Owning the good appeared to increase its value.
Richard Thaler found many examples of what he called the
endowment effect
, especially for goods that are not regularly traded. You can easily imagine yourself in a similar situation. Suppose you hold a ticket to a sold-out concert by a popular band, which you bought at the regular price of $200. You are an avid fan and would have been willing to pay up to $500 for the ticket. Now you have your ticket and you learn on the Internet that richer or more desperate fans are offering $3,000. Would you sell? If you resemble most of the audience at sold-out events you do not sell. Your lowest selling price is above $3,000 and your maximum buying price is $500. This is an example of an endowment effect, and a believer in standard economic theory would be puzzled by it. Thaler was looking for an account that could explain puzzles of this kind.
Chance intervened when Thaler met one of our former students at a conference and obtained an early draft of prospect theory. He reports that he read the manuscript with considerable Bon s Able Bonexcitement, because he quickly realized that the loss-averse value function of prospect theory could explain the endowment effect and some other puzzles in his collection. The solution was to abandon the standard idea that Professor R had a unique utility for the state of
having
a particular bottle. Prospect theory suggested that the willingness to buy or sell the bottle depends on the reference point—whether or not the professor owns the bottle now. If he owns it, he considers the pain of
giving up
the bottle. If he does not own it, he considers the pleasure of
getting
the bottle. The values were unequal because of loss aversion: giving up a bottle of nice wine is more painful than getting an equally good bottle is pleasurable. Remember the graph of losses and gains in the previous chapter. The slope of the function is steeper in the negative domain; the response to a loss is stronger than the response to a corresponding gain. This was the explanation of the endowment effect that Thaler had been searching for. And the first application of prospect theory to an economic puzzle now appears to have been a significant milestone in the development of behavioral economics.
Thaler arranged to spend a year at Stanford when he knew that Amos and I would be there. During this productive period, we learned much from each other and became friends. Seven years later, he and I had another opportunity to spend a year together and to continue the conversation between psychology and economics. The Russell Sage Foundation, which was for a long time the main sponsor of behavioral economics, gave one of its first grants to Thaler for the purpose of spending a year with me in Vancouver. During that year, we worked closely with a local economist, Jack Knetsch, with whom we shared intense interest in the endowment effect, the rules of economic fairness, and spicy Chinese food.
The starting point for our investigation was that the endowment effect is not universal. If someone asks you to change a $5 bill for five singles, you hand over the five ones without any sense of loss. Nor is there much loss aversion when you shop for shoes. The merchant who gives up the shoes in exchange for money certainly feels no loss. Indeed, the shoes that he hands over have always been, from his point of view, a cumbersome proxy for money that he was hoping to collect from some consumer. Furthermore, you probably do not experience paying the merchant as a loss, because you were effectively holding money as a proxy for the shoes you intended to buy. These cases of routine trading are not essentially different from the exchange of a $5 bill for five singles. There is no loss aversion on either side of routine commercial exchanges.
What distinguishes these market transactions from Professor R’s reluctance to sell his wine, or the reluctance of Super Bowl ticket holders to sell even at a very high price? The distinctive feature is that both the shoes the merchant sells you and the money you spend from your budget for shoes are held “for exchange.” They are intended to be traded for other goods. Other goods, such as wine and Super Bowl tickets, are held “for use,” to be consumed or otherwise enjoyed. Your leisure time and the standard of living that your income supports are also not intended for sale or exchange.
Knetsch, Thaler, and I set out to design an experiment that would highlight the contrast between goods that are held for use and for exchange. We borrowed one aspect of the design of our experiment from Vernon Smith, the founder of experimental economics, with whom I would share a Nobel Prize many years later. In this method, a limited number of tokens are distributed to the participants in a “market.” Any participants who own a token at the end Bon s A end Bon of the experiment can redeem it for cash. The redemption values differ for different individuals, to represent the fact that the goods traded in markets are more valuable to some people than to others. The same token may be worth $10 to you and $20 to me, and an exchange at any price between these values will be advantageous to both of us.