What If? (29 page)
Authors: Randall Munroe
Speed Bump
Q.
How fast can you hit a speed bump while driving and live?
—Myrlin Barber
A.
Surprisingly fast.
First, a disclaimer. After reading this answer, don’t try to drive over speed bumps at high speeds. Here are some reasons:
- You could hit and kill someone.
- It can destroy your tires, suspension, and potentially your entire car.
- Have you
read
any of the
other answers in this book?

If that’s not enough, here are some quotes from medical journals on spinal injury from speed bumps.
Examination of the thoracolumbar X-ray and computed tomography displayed compression fractures in four patients . . . Posterior instrumentation was applied . . . All patients recovered well except for the one with cervical fracture.
L1 was the most frequently fractured vertebra
(
23 /52, 44.2 percent
).
Incorporation of the buttocks with realistic properties diminished the first vertical natural frequency from ~12 to 5.5 Hz, in agreement with the literature.
(
Th
at last one isn’t directly related to speed bump injuries, but I wanted to include it anyway.)
Regular little speed bumps probably won’t kill you
Speed bumps are designed to make drivers slow down.
Going over a typical speed bump at 5 miles per hour results in a gentle bounce,
1
while hitting one at 20 delivers a sizable jolt. It’s natural to assume that hitting a speed bump at 60 would deliver a proportionally larger jolt, but it probably wouldn’t.
As those medical quotes attest, it’s true that people are occasionally injured by speed bumps. However, nearly all of those injuries happen
to a very specific category of people: those sitting in hard seats in the backs of buses, riding on poorly maintained roads.
When you’re driving a car, the two main things protecting you from bumps in the road are the tires and the suspension. No matter how fast you hit a speed bump, unless the bump is large enough to hit the frame of the car, enough of the jolt will be absorbed by these two
systems that you probably won’t be hurt.
Absorbing the shock won’t necessarily be
good
for those systems. In the case of the tires, they may absorb it by exploding.
2
If the bump is large enough to hit the wheel rims, it may permanently damage a lot of important parts of the car.
Th
e typical speed bump is between 3 and 4 inches tall.
Th
at’s also about how thick an average tire’s cushion
is (the separation between the bottom of the rims and the ground).
3
Th
is means that if a car hits a small speed bump, the rim won’t actually touch the bump; the tire will just be compressed.
Th
e typical sedan has a top speed of around 120 miles per hour. Hitting a speed bump at that speed would, in one way or another, probably result in losing control of the car and crashing.
4
However, the
jolt
itself
probably wouldn’t be fatal.
If you hit a larger speed bump
—
like a speed hump or speed table
—
your car might not fare so well.
How fast would you have to go to definitely die?
Let’s consider what would happen if a car were going
faster
than its top speed.
Th
e average modern car is limited to a top speed of around 120 mph, and the fastest can go about 200.
While most passenger
cars have some kind of artificial speed limits imposed by the engine computer, the ultimate physical limit to a car’s top speed comes from air resistance.
Th
is type of drag increases with the square of speed; at some point, a car doesn’t have enough engine power to push through the air any faster.
If you
did
force a sedan to go faster than its top speed
—
perhaps by reusing the magical accelerator
from the relativistic baseball
—
the speed bump would be the least of your problems.
Cars generate lift.
Th
e air flowing around a car exerts all kinds of forces on it.
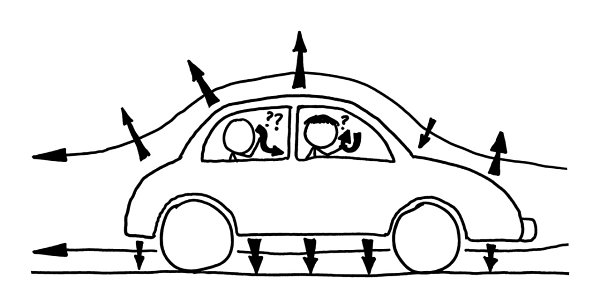
Where did all these arrows come from?
Th
e lift forces are relatively minor at normal highway speeds, but at higher speeds they become substantial.
In a Formula One car equipped with airfoils, this force pushes downward, holding the car against the track. In a sedan, they lift it up.
Among NASCAR fans, there’s frequently talk of a 200-mph “liftoff speed” if the car starts
to spin. Other branches of auto racing have seen spectacular backflip crashes when the aerodynamics don’t work out as planned.
Th
e bottom line is that in the range of 150–300 mph, a typical sedan would lift off the ground, tumble, and crash . . . before you even hit the bump.
BREAKING: Child, Unidentified Creature in Bicycle Basket Hit and Killed by Car
If you kept the car from taking off, the force of the wind at those speeds would strip away the hood, side panels, and windows. At higher speeds, the car itself would be disassembled, and might even burn up like a spacecraft reentering the atmosphere.
What’s the ultimate limit?
In the state
of Pennsylvania, drivers may see $2 added to their speeding ticket for every mile per hour by which they break the speed limit.
Th
erefore, if you drove a car over a Philadelphia speed bump at 90 percent of the speed of light, in addition to destroying the city . . .

. . . you could expect a speeding ticket of $1.14 billion.
- 1
Like anyone with a physics background, I do all my calculations in SI units, but I’ve gotten too many US speeding tickets to write this answer in anything but miles per hour; it’s just been burned into my brain. Sorry!
- 2
Just Google “hit a curb at 60.”
- 3
Th
ere are cars everywhere. Go outside with a ruler and check.
- 4
At high speeds, you can easily lose control even without hitting a bump. Joey Huneycutt’s 220-mph crash left his Camaro a burned-out hulk.
Lost Immortals
Q.
If two immortal people were placed on opposite sides of an uninhabited Earthlike planet, how long would it take them to find each other? 100,000 years? 1,000,000 years? 100,000,000,000 years?
—Ethan Lake
A.
We’ll start with the
simple, physicist-style
1
answer: 3000 years.
Th
at’s about how long it would take two people to find each other, assuming that they
were walking around at random over a sphere for 12 hours per day and had to get within a kilometer to see each other.

We can immediately see some problems with this model.
2
Th
e simplest problem is the assumption that you can always see someone if they come within a kilometer of you.
Th
at’s possible under only the most ideal circumstances; a person walking along a ridge might be visible from a kilometer away, whereas in a thick forest during a rainstorm, two people could pass within a few meters
without seeing each other.
We could try to calculate the average visibility across all parts of the Earth, but then we run into another question: Why would two people who are trying to find each other spend time in a thick jungle? It would seem to make more sense for both of them to stay in flat, open areas where they could easily see and be seen.
3

Once we start considering the psychology of our two people, our spherical-immortal-in-a-vacuum model is in trouble.
4
Why should we assume our people will walk around randomly at all?
Th
e optimal strategy might be something totally different.
What strategy
would
make the most sense for our lost immortals?
If they have time to plan beforehand, it’s easy.
Th
ey can arrange
to meet at the North or South Pole, or
—
if those turn out to be unreachable
—
at the highest point on land, or the mouth of the longest river. If there’s any ambiguity, they can just travel between all the options at random.
Th
ey have plenty of time.
If they don’t have a chance to communicate beforehand, things get a little harder. Without knowing the other person’s strategy, how do you know
what
your
strategy should be?
Th
ere’s an old puzzle, from before the days of cell phones, that goes something like this:
Suppose you’re meeting a friend in an American town that neither of you have been to before. You don’t have a chance to plan a meeting place beforehand. Where do you go?
Th
e author of the puzzle suggested that the logical solution would be to go to the town’s main
post office and wait at the main receiving window, where out-of-town packages arrive. His logic was that it’s the only place that every town in the US has exactly one of, and which everyone would know where to find.
To me, that argument seems a little weak. More importantly, it doesn’t hold up experimentally. I’ve asked that question to a number of people, and none of them suggested the post
office.
Th
e original author of that puzzle would be waiting in the mailroom alone.

Our lost immortals have it tougher, since they don’t know anything about the geography of the planet they’re on.
Following the coastlines seems like a sensible move. Most people live near water, and it’s much faster to search along a line than over a plane. If your guess turns out to be wrong, you won’t have wasted much time compared to having searched the interior first.
Walking around the average continent would take about five years, based on typical width-to-coastline-length ratios for Earth land masses.
5
Let’s assume you and the other person are on the same continent. If you both walk counterclockwise, you could circle forever without finding each other.
Th
at’s no good.
A different approach would be to make a complete circle counterclockwise, then
flip a coin. If it comes up heads, circle counterclockwise again. If tails, go clockwise. If you’re both following the same algorithm, this would give you a high probability of meeting within a few circuits.
Th
e assumption that you’re both using the same algorithm is probably optimistic. Fortunately, there’s a better solution: Be an ant.
Here’s the algorithm that I would follow (if you’re
ever lost on a planet with me, keep this in mind!):
If you have no information, walk at random, leaving a trail of stone markers, each one pointing to the next. For every day that you walk, rest for three. Periodically mark the date alongside the cairn. It doesn’t matter how you do this, as long as it’s consistent. You could chisel the number of days into a rock, or lay out rocks to plot the
number.

If you come across a trail that’s newer than any you’ve seen before, start following it as fast as you can. If you lose the trail and can’t recover it, resume leaving your own trail.
You don’t have to come across the other player’s current location; you simply have to come across a location where they’ve been. You can still chase one another in circles, but as long as you move more quickly
when you’re following a trail than when you’re leaving one, you’ll find each other in a matter of years or decades.
And if your partner isn’t cooperating
—
perhaps they’re just sitting where they started and waiting for you
—
then you’ll get to see some neat stuff.

- 1
Assuming a spherical immortal human in a vacuum . . .
- 2
Like, what happened to all the other people? Are they okay?
- 3
Although the visibility calculation
does
sounds fun. I know what I’m doing next Saturday night!
- 4
Which is why we usually try not to consider things like that.
- 5
Of course, some areas would present a challenge. Louisiana’s bayous, the Caribbean’s mangrove forests, and Norway’s fjords would all make for slower walking than a typical beach.