XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition (361 page)
Read XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition Online
Authors: Michael Kay
Existential Comparison
The peculiar property of these operators, namely that A = B is true if there is an item in A that is equal to an item in B, is sometimes called
existential semantics
—the operator is testing for the existence of a matching pair of items. This section explores the consequences of this rule..
Where a sequence
$N
is compared with a string
“Mary”
, the test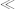 $N=“Mary”
$N=“Mary”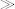 is effectively a shorthand for “if there is an item
is effectively a shorthand for “if there is an item
$n
in
$N
such that
$n
eq
“Mary”
”. Similarly, the test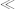 $N!=“Mary”
$N!=“Mary”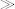 is effectively a shorthand for “if there is an item
is effectively a shorthand for “if there is an item
$n
in
$N
such that
$n
ne
‘Mary’
”. If
$N
contains two items, whose values are “
Mary
” and “
John
”, then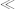 $N=‘Mary’
$N=‘Mary’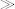 and
and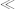 $N!=‘Mary’
$N!=‘Mary’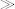 will both be true, because there is an item that is equal to
will both be true, because there is an item that is equal to
‘Mary’
and another that is not. If
$N
is an empty sequence, then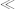 $N=‘Mary’
$N=‘Mary’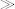 and
and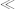 $N!=‘Mary’
$N!=‘Mary’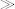 will both be false, because there is no item that is equal to
will both be false, because there is no item that is equal to
‘Mary’
, but there is also no item that is not equal to
‘Mary’
.
Note that when the operand is a sequence of nodes, we are only concerned with the nodes that are members of the sequence in their own right. The children of these nodes are not members of the sequence. So if
$N
is the element:
then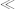 $N=“Mary”
$N=“Mary”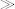 will not return true. In this case $N is a singleton sequence. Its only item is the
will not return true. In this case $N is a singleton sequence. Its only item is the
“Mary”
. In fact, with a schema-aware processor this comparison might well throw an error, on the grounds that the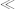 $N/person=“Mary”
$N/person=“Mary”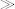 . In this expression,
. In this expression,
$N/person
is a sequence of two
“Mary”
.