Against the Gods: The Remarkable Story of Risk (50 page)

The mathematics of diversification helps to explain its attraction.
While the return on a diversified portfolio will be equal to the average
of the rates of return on its individual holdings, its volatility will be less
than the average volatility of its individual holdings. This means that
diversification is a kind of free lunch at which you can combine a group
of risky securities with high expected returns into a relatively low-risk
portfolio, so long as you minimize the covariances, or correlations,
among the returns of the individual securities.

Until the 1990s, for example, most Americans regarded foreign securities as too speculative and too difficult to manage to be appropriate
investments. So they invested just about all their money at home. That
parochial view was costly, as the following calculations demonstrate.

From 1970 to 1993, the Standard & Poor's Index of 500 stocks
brought its investors a total of capital appreciation plus income that
averaged 11.7% a year. The volatility of the Index's return, as measured
by its standard deviation, averaged 15.6% a year; this meant that about
two-thirds of the annual returns fell between 11.7% + 15.6%, or 27.3%
on the high side, and 11.7% - 15.6%, or -3.9% on the low side.

The major markets outside the United States are usually tracked by
an index published by Morgan Stanley & Company that covers Europe,
Australia, and the Far East. This index is known as EAFE for short; the
regulars in these markets pronounce it "Eee-fuh." EAFE's average
annual return for a dollar-based investor from 1970 to 1993 was 14.3%
versus S&P's 11.7%, but EAFE was also more volatile. Largely because
of Japan, and because foreign market returns are translated back into a dollar that fluctuates in value in the foreign exchange markets, EAFE's
standard deviation of 17.5% was over two full percentage points above
the volatility of the S&P 500.

EAFE and the U.S. markets do not usually move up and down
together, which is why international diversification makes good sense. If
an investor's portfolio had held 25% of its assets in EAFE and 75% in the
S&P since 1970, its standard deviation of 14.3% would have been lower
than either the S&P or EAFE, even while it was producing an average
return that bettered the S&P 500 alone by an average of 0.6% a year.

An even more dramatic illustration of the power of diversification
appears in the accompanying chart, which shows the track record of
13 so-called emerging stock markets in Europe, Latin America, and
Asia from January 1992 through June 1994. The average monthly
return of each market is plotted on the vertical axis; each market's monthly standard deviation of return is plotted on the horizontal axis.
The chart also shows an equally weighted index of the 13 markets as
well as the performance of the S&P 500 over the same time period.

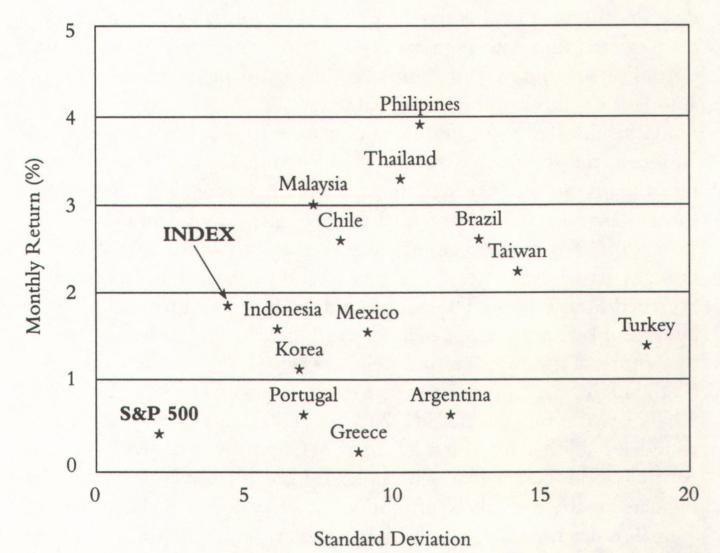
The blessings of diversification. The track records of 13 emerging stock markets
compared to the index (average of 13) and the S&P 500 from January 1992
through June 1994. The data are in percentages per month.

Although many investors think of emerging markets as a homogeneous group, the graph shows that these 13 markets tend to be largely independent of one another. Malaysia, Thailand, and the Philippines had returns of 3% a month or better, but Portugal, Argentina, and Greece were barely in the black. Volatilities ranged from about 6% all the way out to nearly 20% a month. There is plenty of heat in this oven.

The lack of correlation, or low covariance, among the markets caused the index to have the lowest standard deviation of any of its 13 components. A simple average of the monthly standard deviations of the twelve markets works out to 10.0%; the actual standard deviation of the diversified portfolio was only 4.7%. Diversification works.

Note that the emerging markets were much riskier than the U.S. stock market over this 18-month period. They were also a lot more profitable, which explains why investors were so enthusiastic about these markets at the time.

The riskiness of these markets came to light just eight months after the end of the time period covered here. Had the analysis been extended to February 1995, it would have included the Mexican debacle at the end of 1994; the Mexican market fell by 60% between June 1994 and February 1995. From January 1992 to February 1995, the average return of the 13 markets was only a little over 1% a month, down from nearly 2% during the time span shown on the chart, while the standard deviation of the index jumped from under 5% to 6% a month; an investor in Mexico and Argentina would have ended up losing money.*
The Philipines, the best-performing market, dropped from 4% a month to only 3% a month. Meanwhile, the performance of the S&P 500 showed virtually no change at all.

By substituting a statistical stand-in for crude intuitions about
uncertainty, Markowitz transformed traditional stock-picking into a
procedure for selecting what he termed "efficient" portfolios. Efficiency, a term adopted from engineering by economists and statisticians, means maximizing output relative to input, or minimizing input
relative to output. Efficient portfolios minimize that "undesirable
thing" called variance while simultaneously maximizing that "desirable
thing" called getting rich. This process is what prompted Tschampion
30 years later to describe the managers of the General Motors pension
fund as "engineers."

Investors will always want to own securities that represent "the best
at the price." The expected return of a portfolio made up of such securities will be the mean, or average, of the expectations for each of the
individual holdings. But holdings that appear to offer the best returns
frequently disappoint while others exceed the investor's fondest hopes.
Markowitz assumed that the probabilities of actual portfolio returns
above and below the mean expectation will distribute themselves into a
nice, symmetrically balanced Gaussian normal curve.

The spread of that curve around the mean, from loss to gain,
reflects the variance of the portfolio-with the range of possible outcomes reflecting the likelihood that the portfolio's actual rate of return
will differ from its expected rate of return. This is what Markowitz
meant when he introduced the concept of variance to measure risk, or
the uncertainty of return; the combined approach to risk and return is
commonly referred to by professionals and academics as mean/variance
optimization. Common stocks have a much wider range of possible
results than an obligation of the U.S. Treasury that will come due and
pay off in 90 days; the return on the Treasury obligation has almost no
uncertainty, because buyers will see their money again so soon.

Markowitz reserved the term "efficient" for portfolios that combine the best holdings at the price with the least of the variance"optimization" is the technical word. The approach combines two
cliches that investors learn early in the game: nothing ventured, nothing gained, but don't put all your eggs in one basket.

It is important to recognize that there is no one efficient portfolio
that is more efficient than all others. Thanks to linear programing,
Markowitz's method produces a menu of efficient portfolios. Like any
menu, this one has two sides: what you want is on one side and the cost of what you want is on the other. The higher the expected return, the
greater the risks involved. But each efficient portfolio on the menu will
have the highest expected return for any given level of risk or the lowest
level of risk for any expected return.

Rational investors will select the portfolio that best suits their taste
for either aggressive objectives or defensive objectives. In the tradition
of von Neumann and Morgenstern, the system provides a method to
maximize each investor's utility. This is the only point in the Markowitz
system in which gut matters. All else is measurement.

"Portfolio Selection" revolutionized the profession of investment
management by elevating risk to equal importance with expected return.
That paper, together with the book by the same name that Markowitz
wrote in 1959, provided the groundwork for just about all of the theoretical work in finance that followed. It has also supported a variety of
applications over time, ranging from techniques of stock selection and the
allocation of portfolios between stocks and bonds to the valuation and
management of options and more complex derivative securities.

Despite its importance, critics of "Portfolio Selection" have turned
Markowitz's work into a punching bag, attacking from every side the
entire set of assumptions that support it. Some of the problems they
have raised are more mechanical and technical than substantive and
have been overcome. Other problems continue to stir controversy.

The first is whether investors are rational enough in their decisionmaking to follow the prescription that Markowitz set out for them. If
intuition triumphs over measurement in investing, the whole exercise
could turn out to be a waste of time and a flawed explanation of why
markets behave as they do.

Another criticism questions whether variance is the proper proxy
for risk. Here the consequences are less clear. If investors perceive risk
as something different from variance, some other measure might serve
equally well and still preserve Markowitz's optimizing approach to risk
and return. And perhaps not.

Finally, what would happen if Markowitz's assumption that there is
a positive relationship between risk and return fails to survive empirical
tests? If high returns are systematically available on low-risk securities, or if you land in the soup with securities you thought were low-risk,
a retreat to the drawing board will be necessary.

We shall deal here briefly with the technical problems and then at
greater length with the question of how well variance serves as a proxy
for risk. Investor rationality is so important a matter that we devote
Chapters 16 and 17 to it; investors, after all, are just people, although
engaged in a particular activity, which means that the whole question
of human rationality is involved.

The technical problems arise from Markowitz's assumption that
investors will have no difficulty estimating the inputs to his modelexpected returns, variances, and the covariances among all the individual holdings. But, as Keynes emphasized in A Treatise on Probability and
later as well, the use of data from the past is dangerous. And degrees of
belief do not always lend themselves to precise measurement, particularly with the precision that the Markowitz approach requires. As a
practical matter, most applications of the approach combine past experience with forecasts, though investors recognize that a significant margin of error surrounds the results of such calculations. In addition, the
sensitivity of the process to small differences in estimates of the inputs
makes the results even more tentative.

The most difficult step is in amassing the calculations required to
measure how each individual stock or bond might vary in relation to
each other stock or bond. William Baumol, the author of the paper
demonstrating how long-term trends in productivity regress to the
mean, calculated as late as 1966-fourteen years after the appearance of
"Portfolio Selection"-that a single run to select efficient portfolios on
the computers of that time would cost from $150 to $350, even assuming that the estimates of the necessary inputs were accurate. A more
elaborate search would have run into thousands of dollars.'