Authors: Michael Kaplan
Chances Are (2 page)
All men are mortal.
Socrates is a man.
Therefore Socrates is mortal.
Socrates is a man.
Therefore Socrates is mortal.
Â
This
must
be so; the conclusion is built into the definitions. Aristotle's syllogisms defined the science of reasoning from his own time right up to the beginning of the seventeenth century. But there is an essential flaw in deductive reasoning: the difference between the
valid
and the
true
. The rules for constructing a syllogism tell you whether a statement is logically consistent with the premises, but they tell you nothing about the premises themselves. The Kamchatkans believe that volcanoes are actually underground feasting places where demons barbecue whales: if a mountain is smoking, the demons are having a party; there is nothing
logically
wrong with this argument. So deductive logic is confined to describing relations between labels, not necessarily truths about things. It cannot make something from nothing; like a glass of water for Japanese paper flowers, it simply allows existing relationships to unfold and blossom. Today, its most widespread application is in the logic chip of every computer, keeping the details of our lives from crashing into contradiction. But, as computer experts keep telling us, ensuring that the machines are not fed garbage is our responsibility, not theirs. The premises on which automated logic proceeds are themselves the result of human conclusions about the nature of the worldâand those conclusions cannot be reached through deduction alone.
must
be so; the conclusion is built into the definitions. Aristotle's syllogisms defined the science of reasoning from his own time right up to the beginning of the seventeenth century. But there is an essential flaw in deductive reasoning: the difference between the
valid
and the
true
. The rules for constructing a syllogism tell you whether a statement is logically consistent with the premises, but they tell you nothing about the premises themselves. The Kamchatkans believe that volcanoes are actually underground feasting places where demons barbecue whales: if a mountain is smoking, the demons are having a party; there is nothing
logically
wrong with this argument. So deductive logic is confined to describing relations between labels, not necessarily truths about things. It cannot make something from nothing; like a glass of water for Japanese paper flowers, it simply allows existing relationships to unfold and blossom. Today, its most widespread application is in the logic chip of every computer, keeping the details of our lives from crashing into contradiction. But, as computer experts keep telling us, ensuring that the machines are not fed garbage is our responsibility, not theirs. The premises on which automated logic proceeds are themselves the result of human conclusions about the nature of the worldâand those conclusions cannot be reached through deduction alone.
Â
You'll remember that the other awkward question from the back seat was “What if it's not like that?” Instinctively, we reason from example to principle, from objects to qualities. We move from seeing experience as a mere bunch of random stuff to positing the subtly ordered web of cause and effect that keeps us fascinated through a lifetime. But are we justified in doing so? What makes our assumptions different from mere prejudice?
Sir Francis Bacon fretted over this question at the turn of the seventeenth century, projecting a new science, cut loose from Aristotle's apron strings and ready to see, hear, feel, and conclude for itself using a method he called “induction.” Bacon was Lord Chancellor, the senior judge of the realm, and he proceeded in a lawyerly way, teasing out properties from experience, then listing each property's positive and negative instances, its types and degrees. By cutting through experience in different planes, he hoped to carve away all that was inessential. Science, in his scheme, was like playing “twenty questions” or ordering a meal in a foreign language: the unknown relation was defined by indirection, progressively increasing information by attempting to exclude error.
Induction actually has three faces, each turned a slightly different way. The homely village version is our most natural form of reasoning: the proverb. “Don't insult an alligator until you're over the creek”; “A friend in power is no longer your friend.” Everything your daddy told you is a feat of induction, a crystal of permanent wisdom drawn out of the saturated solution of life.
Induction's second, more exalted face is mathematical: a method of amazing power that allows you to fold up the infinite and put it in your pocket. Let's say you want to prove that the total of the first
n
odd numbers, starting from 1, is
n
2
. Try it for the first three: 1 + 3 + 5 = 9 = 3
2
; so far, so good. But you don't want to keep checking individual examples; you want to know if this statement is true or false over
all
examplesâthe first billion odd numbers, the first googol odd numbers.
n
odd numbers, starting from 1, is
n
2
. Try it for the first three: 1 + 3 + 5 = 9 = 3
2
; so far, so good. But you don't want to keep checking individual examples; you want to know if this statement is true or false over
all
examplesâthe first billion odd numbers, the first googol odd numbers.
Why not start by proving the case for the first odd number, 1? Easy: 1 = 1
2
. Now
assume
that the statement is true for an abstract number
n;
that is: 1 + 3 + 5 + . . . up to
n
odd numbers will equal
n
2
. It would probably help if we defined what the
n
th odd number is: well, the
n
th even number would be 2
n
(since the evens are the same as the 2 times table), so the
n
th odd number is 2
n
â1 (since the first odd, 1, comes before the first even, 2). Now we need to show that
if
the statement is true for the
n
th odd number, it will also be true for the
n
+ 1st; that is:
2
. Now
assume
that the statement is true for an abstract number
n;
that is: 1 + 3 + 5 + . . . up to
n
odd numbers will equal
n
2
. It would probably help if we defined what the
n
th odd number is: well, the
n
th even number would be 2
n
(since the evens are the same as the 2 times table), so the
n
th odd number is 2
n
â1 (since the first odd, 1, comes before the first even, 2). Now we need to show that
if
the statement is true for the
n
th odd number, it will also be true for the
n
+ 1st; that is:
Â
Assuming that
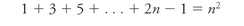
show that
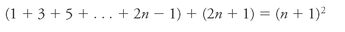
Let's look more closely at that (
n
+ 1)
2
on the right. If we do the multiplication, it comes out as
n
2
+ 2
n
+ 1. But wait a minute: that's the same as
n
2
, the sum of the first
n
odd numbers, plus 2
n
+ 1, the next odd number. So if our statement is true for
n
odd numbers it
must
be true for
n
+ 1.
n
+ 1)
2
on the right. If we do the multiplication, it comes out as
n
2
+ 2
n
+ 1. But wait a minute: that's the same as
n
2
, the sum of the first
n
odd numbers, plus 2
n
+ 1, the next odd number. So if our statement is true for
n
odd numbers it
must
be true for
n
+ 1.
But, you may be asking, aren't you just proving a relation between two imaginary things? How is this different from deduction? It's different because we already know the statement is true for the first odd number, 1. Set
n
equal to 1; now we know it's true for the second odd, 3; so we can set
n
equal to 2, proving the statement for the next odd, 5âand so on. We don't need to look at every example, because all the examples are equivalent; we have constructed a rule that governs them all under the abstract title
n
. Away they go, like a row of dominoes, rattling off to infinity.
n
equal to 1; now we know it's true for the second odd, 3; so we can set
n
equal to 2, proving the statement for the next odd, 5âand so on. We don't need to look at every example, because all the examples are equivalent; we have constructed a rule that governs them all under the abstract title
n
. Away they go, like a row of dominoes, rattling off to infinity.
The third, inscrutable, face of induction is scientific. Unfortunately, very little in the observable world is as easily defined as an odd number. Science would be so much simpler if we could consider protons, or prions, or pandas under an abstract
p
and show that anything true for one is bound to be true for
p
+ 1. But of course we can'tâand this is where probability becomes a necessity: the things we are talking about, the forms applied to matter, are, like Aristotle's axioms, defined not by themselves but by us. A number or a geometrical form is its own definitionâa panda isn't.
p
and show that anything true for one is bound to be true for
p
+ 1. But of course we can'tâand this is where probability becomes a necessity: the things we are talking about, the forms applied to matter, are, like Aristotle's axioms, defined not by themselves but by us. A number or a geometrical form is its own definitionâa panda isn't.
Our approach to science follows Bacon's: look and see, question and test. But there are deep questions hiding below these simple instructions. What are you looking for? Where should you look? How will you know you've found it? How will you find it again? Every new observation brings with it a freight of information: some of it contains the vital fact we need for drawing conclusions, but some is plain error. How do we distinguish the two? By getting a sense of likely variation.
This makes scientific induction a journey rather than an arrival; while every example we turn up may confirm the assumption we have made about a cause, we will still never reach ultimate truth. Without repetition we could never isolate qualities from experience, but repetition on its own proves nothing. Simply saying “The sun is bright” requires, in all honesty, the New Englander's reply “Yepâso far.”
Â
All swans are whiteâuntil you reach Australia and discover the black swans paddling serenely. For science built on induction, the counterexample is always the ruffian waiting to mug innocent hypotheses as they pass by, which is why the scientific method now deliberately seeks him out, sending assumptions into the zone of maximum danger. The best experiments deduce an effect from the hypothesis and then isolate it in the very context where it may be disproved. This falsifiability is what makes a hypothesis different from a beliefâand science distinct from the other towers of opinion.
For everyone, not just scientists, induction poses a further problem: we need to act on our conclusions. For those of us who must venture out into the world, wagering our goods on uncertain expectations, the counterexample could well be the storm that sinks our ship, the war that wrecks our country. In human affairs, we cannot hope either to predict with certainty or to test with precision, so we instead try to match the complexity of the moment with the complexity of memory, of imagination, and of character. In studying history we are doing induction of a kitchen rather than laboratory style. When Plutarch contrasted the characters of great Greeks and Romans, or Thomas à Kempis urged us to imitate Christ in all things, they were setting out a line of reasoning by which the complexities of life, seen through the equally complex filter of a virtuous character, could resolve into a simpler decision.
But now that our village walls encompass the whole world, we have exemplars ranging from Mahatma Gandhi to General Patton, which shows the weakness of a purely humanist form of induction. We need a method of reasoning that can offer both the accountability of science and the humanities' openness to untidy, fascinating life. If it is to be accountable, it needs a way to make clear, falsifiable statements, or we are back wrangling with the Sophists. If it is to reflect life, it needs to embrace uncertainty, since that, above all else, is our lot.
Woe's me! woe's me! In Folly's mailbox
Still laughs the postcard, Hope:
Your uncle in Australia
Has died and you are Pope,
For many a soul has entertained
A mailman unawaresâ
And as you cry, Impossible,
A step is on the stairs.
Still laughs the postcard, Hope:
Your uncle in Australia
Has died and you are Pope,
For many a soul has entertained
A mailman unawaresâ
And as you cry, Impossible,
A step is on the stairs.
âRandall Jarrell
Â
The science of uncertainty is probability; it deals with what is repeated but inconsistent. Its statements are not the definitive
all
or
no
of deductive logic but the nuanced:
most
,
hardly
,
sometimes
, and
perhaps
. It separates
normal
from
exceptional
,
predictable
from
random
and determines whether an action is “worth it.” It is the science of risk, conjecture, and expectationâthat is, of getting on with life.
all
or
no
of deductive logic but the nuanced:
most
,
hardly
,
sometimes
, and
perhaps
. It separates
normal
from
exceptional
,
predictable
from
random
and determines whether an action is “worth it.” It is the science of risk, conjecture, and expectationâthat is, of getting on with life.
Yes, but why does probability have to be numerical? Both laypeople and mathematicians groan at the mere mention of probabilityâthe mathematicians because the messiness of the subject seems to sully the discipline itself, leaving it provisional and tentative, a matter of recipes rather than discoveries; and laypeople for the excellent reason that it's hard to see the value for real life in an expression like:
 And yet this is an important statement about the way we come to believe things.
And yet this is an important statement about the way we come to believe things.

Abstraction, modelingâputting interesting things in numerical termsâcan seem like freeze-drying, leaving the shape of life without the flavor. But there is no avoiding number. It is needed to set real things in order, to compare across variety of experience, to handle extremes of scale, and to explore regions our intuition cannot easily enter. It is not intrinsically more
true
than other kinds of discourseâa mortality table is no closer to life than is
Death in Venice
. Nor is speaking numerically a cure for speaking nonsense, although it does offer a more convenient way to detect nonsense once it is said. Numbers make statements about likelihood falsifiable, extend our understanding of experience beyond our local habitation to the extremes of time and space, and give us an elastic frame of reference, equally suitable to this room and the universe, this instant and eternity.
true
than other kinds of discourseâa mortality table is no closer to life than is
Death in Venice
. Nor is speaking numerically a cure for speaking nonsense, although it does offer a more convenient way to detect nonsense once it is said. Numbers make statements about likelihood falsifiable, extend our understanding of experience beyond our local habitation to the extremes of time and space, and give us an elastic frame of reference, equally suitable to this room and the universe, this instant and eternity.
Other books
Rising Tides by Taylor Anderson
Wench With Wings by Cassidy, Rose D.
Pistols at Dawn by Andrea Pickens
If the Shoe Fits (Whatever After #2) by Sarah Mlynowski
The Darkfall Switch by David Lindsley
House of Trembling Leaves, The by Lees, Julian
Black Dust Mambo by Adrian Phoenix
The Killing Game by Anderson, Toni
Secrets of the Heart by Jillian Kent
Front of House: Observations from a Decade on the Aisle by Denise Reich