Data Mining (52 page)

While the gain criterion has had some good results in the construction of compact decision trees, it also has one serious deficiency: a strong bias in favor of tests with many outcomes. A solution was found in some kinds of normalization. By analogy with the definition of Info(S), an additional parameter was specified:

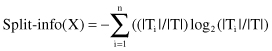
This represented the potential information generated by dividing set T into n subsets T
_i
. Now, a new gain measure could be defined:

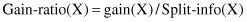
This new gain measure expresses the proportion of information generated by the split that is useful, that is, that appears helpful in classification. The gain-ratio criterion also selects a test that maximizes the ratio given earlier. This criterion is robust and typically gives a consistently better choice of a test than the previous gain criterion. A computation of the gain-ratio test can be illustrated for our example. To find the gain-ratio measure for the test x
₁
, an additional parameter Split-info(x
₁
) is calculated:

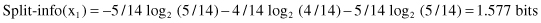
A similar procedure should be performed for other tests in the decision tree. Instead of gain measure, the maximal gain ratio will be the criterion for attribute selection, along with a test to split samples into subsets. The final decision tree created using this new criterion for splitting a set of samples will be the most compact.

6.3 UNKNOWN ATTRIBUTE VALUES

The previous version of the C4.5 algorithm is based on the assumption that all values for all attributes are determined. But in a data set, often some attribute values for some samples can be missing—such incompleteness is typical in real-world applications. This might occur because the value is not relevant to a particular sample, or it was not recorded when the data were collected, or an error was made by the person entering data into a database. To solve the problem of missing values, there are two choices:

The first solution is simple but unacceptable when large amounts of missing values exist in a set of samples. To address the second alternative, several questions must be answered:

All these and many other questions arise with any attempt to find a solution for missing data. Several classification algorithms that work with missing data are usually based on filling in a missing value with the most probable value, or on looking at the probability distribution of all values for the given attribute. None of these approaches is uniformly superior.

In C4.5, it is an accepted principle that samples with unknown values are distributed probabilistically according to the relative frequency of known values. Let Info(T) and Info
_x
(T) be calculated as before, except that only samples with known values of attributes are taken into account. Then the gain parameter can reasonably be corrected with a factor F, which represents the probability that a given attribute is known (F = number of samples in the database with a known value for a given attribute/total number of samples in a data set). The new gain criterion will have the form

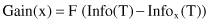
Similarly, Split-info(x) can be altered by regarding the samples with unknown values as an additional group in splitting. If the test x has n outcomes, its Split-info(x) is computed as if the test divided the data set into n + 1 subsets. This modification has a direct influence on the final value of the modified criterion Gain-ratio(x).

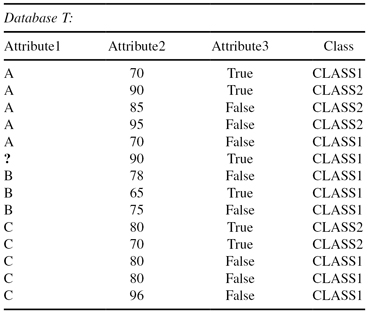
Let us explain the modifications of the C4.5 decision-tree methodology applied on one example. The database is similar to the previous one (Table
6.1
), only there is now one value missing for Attribute1 denoted by “?” as presented in Table
6.2
.

TABLE 6.2.
A Simple Flat Database of Examples with One Missing Value

The computation of the gain parameter for Attribute1 is similar to as before, only the missing value corrects some of the previous steps. Eight out of the 13 cases with values for Attribute1 belong to CLASS1 and five cases to CLASS2, so the entropy before splitting is

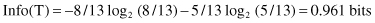
After using Attribute1 to divide T into three subsets (test x
₁
represents the selection one of three values A, B, or C), the resulting information is given by

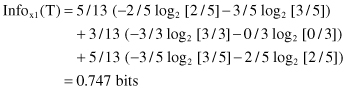
The information gained by this test is now corrected with the factor F (F = 13/14 for our example):

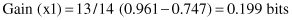
The gain for this test is slightly lower than the previous value of 0.216 bits. The split information, however, is still determined from the entire training set and is larger, since there is an extra category for unknown values.