How to Read a Paper: The Basics of Evidence-Based Medicine (22 page)

I had trouble explaining to the window cleaner that the test result did not necessarily mean this at all, any more than a guilty verdict
necessarily
makes someone a murderer. The definition of diabetes, according to the World Health Organisation (WHO), is a blood glucose level above 7 mmol/l in the fasting state, or above 11.1 mmol/l 2 h after a 100 g oral glucose load (the much-dreaded ‘glucose tolerance test’, where the participant has to glug down every last drop of a sickly glucose drink and wait 2 h for a blood test) [1]. These values must be achieved on two separate occasions if the person has no symptoms, but on only one occasion if they have typical symptoms of diabetes (thirst, passing large amounts of urine, etc.).

These stringent criteria can be termed the
gold standard
for diagnosing diabetes. In other words, if you fulfil the WHO criteria you can call yourself diabetic, and if you don't, you can't (although note that official definitions of what is and isn't a disease change regularly—and indeed, every time I produce a new edition of this book I have to see whether the ones I have cited have changed in the light of further evidence). The same cannot be said for dipping a stick into a random urine specimen. For one thing, you might be a true diabetic but have a high renal threshold—that is, your kidneys conserve glucose much better than most people's, so your blood glucose level would have to be much higher than most people's for any glucose to appear in your urine. Alternatively, you may be an otherwise normal individual with a
low
renal threshold, so glucose leaks into your urine even when there isn't any excess in your blood. In fact, as anyone with diabetes will tell you, diabetes is very often associated with a negative test for urine glucose.

There are, however, many advantages in using a urine dipstick rather than the full-blown glucose tolerance test to ‘screen’ people for diabetes. The test is inexpensive, convenient, easy to perform and interpret, acceptable to patients and gives an instant, yes/no result. In real life, people like my window cleaner may decline to take an oral glucose tolerance test—especially if they are self-employed and asked to miss a day's work for the test. Even if he was prepared to go ahead with it, his GP might decide (rightly or wrongly) that the window cleaner's symptoms did not merit the expense of this relatively sophisticated investigation. I hope you can see that even though the urine test cannot say for sure if someone is diabetic, it has something of a practical edge over the gold standard. That, of course, is why people use it!

In order to assess objectively just how useful the urine glucose test for diabetes is, we would need to select a sample of people (say, 100) and do two tests on each of them: the urine test (screening test), and a standard glucose tolerance test (gold standard). We could then see, for each person, whether the result of the screening test matched the gold standard. Such an exercise is known as a
validation study
. We could express the results of the validation study in a two-by-two table (also known as a
two-by-two matrix
) as in
Figure 8.2
, and calculate various features of the test as in
Table 8.1
, just as we did for the features of the jury in section ‘Complex interventions’.

Figure 8.2
2 × 2 table notation for expressing the results of a validation study for a diagnostic or screening test.

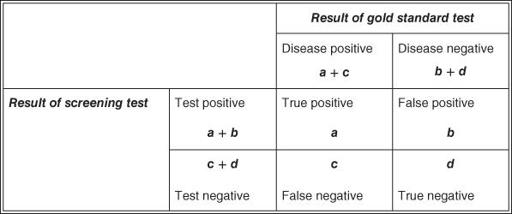
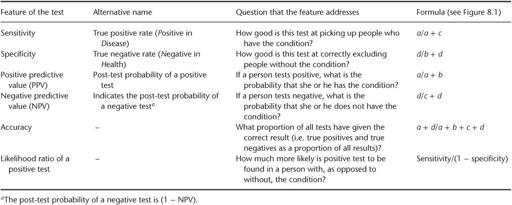
Table 8.1
Features of a diagnostic test, which can be calculated by comparing it with a gold standard in a validation study

If the values for the various features of a test (such as sensitivity and specificity) fell within reasonable limits, we would be able to say that the test was
valid
(see Question Seven). The validity of urine testing for glucose in diagnosing diabetes was assessed many years ago by Andersson and colleagues [2], whose data I have used in the example in
Figure 8.3
. In fact, the original study was performed on 3268 participants, of whom 67 either refused to produce a specimen or, for some other reason, were not adequately tested. For simplicity's sake, I have ignored these irregularities and expressed the results in terms of a denominator (total number tested) of 1000 participants.

In actual fact, these data came from an epidemiological survey to detect the prevalence of diabetes in a population; the validation of urine testing was a side issue to the main study. If the validation had been the main aim of the study, the participants selected would have included far more diabetic individuals, as Question Two in will show [2]. If you look up the original paper, you will also find that the gold standard for diagnosing true diabetes was not the oral glucose tolerance test but a more unconventional series of observations. Nevertheless, the example serves its purpose, as it provides us with some figures to put through the equations listed in the last column of
Table 8.1
. We can calculate the important features of the urine test for diabetes as follows:

a.
sensitivity =
a
/(
a
+
c
) = 6/27 = 22.2%;

b.
specificity =
d
/(
b
+
d
) = 966/973 = 99.3%;

c.
positive predictive value =
a
/(
a
+
b
) = 6/13 = 46.2%;

d.
negative predictive value =
d
/(
c
+
d
) = 966/987 = 97.9%;

e.
accuracy = (
a
+
d
)/(
a
+
b
+
c
+
d
) = 972/1000 = 97.2%;

f.
likelihood ratio of a positive test = sensitivity/(1 − specificity) = 22.2/0.7 = 32;

g.
likelihood ratio of a negative test = (1 − sensitivity)/specificity = 77.8/99.3 = 0.78.

Figure 8.3
2 × 2 table showing results of a validation study of urine glucose testing for diabetes against the gold standard of glucose tolerance test (based on Andersson et al. [2]).

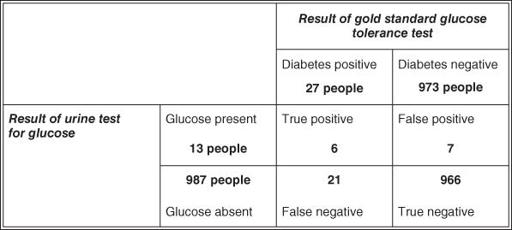
From these features, you can probably see why I did not share the window cleaner's assurance that he did not have diabetes. A positive urine glucose test is only 22% sensitive, which means that the test misses nearly four-fifths of people who really do have diabetes. In the presence of classical symptoms and a family history, the window cleaner's baseline odds (pre-test likelihood) of having the condition are pretty high, and they are only reduced to about four-fifths of this (the negative likelihood ratio, 0.78; see section ‘Likelihood ratios’) after a single negative urine test. In view of his symptoms, this man clearly needs to undergo a more definitive test for diabetes [3]. Note that as the definitions in
Table 8.1
show, if the test had been positive the window cleaner would have good reason to be concerned, because even though the test is not very
sensitive
(i.e. it is not good at picking up people with the disease), it is pretty
specific
(i.e. it
is
good at excluding people without the disease).

Despite the findings of these studies from almost 20 years ago, urine testing to ‘exclude diabetes’ is still shockingly common in some settings. But the academic argument has long shifted to the question of whether the HbA1c blood test is sufficiently sensitive and specific to serve as a screening test for diabetes [4] [5]. The arguments have become far more complex as epidemiologists have weighed in with evidence on early (subclinical) microvascular damage, but the essential principles of the 2 × 2 matrix and the questions about false positives and false negatives still apply. In short, the test performs very well—but it does require a blood test and the costs are not insignificant.

Students often get mixed up about the sensitivity/specificity dimension of a test and the positive/negative predictive value dimension. As a rule of thumb, the sensitivity or specificity tells you about the
test in general
, whereas the predictive value tells you about
what a particular test result means for the patient in front of you
. Hence, sensitivity and specificity are generally used more by epidemiologists and public health specialists whose day-to-day work involves making decisions about
populations
.

A screening mammogram (breast X-ray) might have an 80% sensitivity and a 90% specificity for detecting breast cancer, which means that the test will pick up 80% of cancers and exclude 90% of women without cancer. But imagine you were a GP or practice nurse and a patient comes to see you for the result of her mammogram. The question she will want answered is (if the test has come back positive), ‘What is the chance that I’ve got cancer?' or (if it has come back negative) ‘What is the chance that I can now forget about the possibility of cancer?’ Many patients (and far too many health professionals) assume that the negative predictive value of a test is 100%—that is, if the test is ‘normal’ or ‘clear’ they think there is no chance of the disease being present—and you only need to read the confessional stories in women's magazines (‘I was told I had cancer but tests later proved the doctors wrong’) to find examples of women who have assumed that the positive predictive value of a test is 100%.

Ten questions to ask about a paper that claims to validate a diagnostic or screening test

In preparing these tips, I have drawn on three main published sources: the Users' Guides to the Medical Literature [6] [7]; a more recent article by some of the same authors [8] and Mant's [9] simple and pragmatic guidelines for ‘testing a test’. Like many of the checklists in this book, these are no more than pragmatic rules-of-thumb for the novice critical appraiser: for a much more comprehensive and rigorously developed set of criteria (which runs to a daunting 234 pages) known as the
QADAS
(Quality in Diagnostic and Screening tests) checklist, see a recent review by the UK Health Technology Assessment Programme [8]. Lucas and colleagues [10] have since produced a checklist that is similar but not identical to the questions listed here.

Question One: Is this test potentially relevant to my practice?

This is the ‘so what?’ question, which epidemiologists call the
utility
of the test. Even if this test were 100% valid, accurate and reliable, would it help me? Would it identify a treatable disorder? If so, would I use it in preference to the test I use now? Could I (or my patients or the taxpayer) afford it? Would my patients consent to it? Would it change the probabilities for competing diagnoses sufficiently for me to alter my treatment plan? If the answers to these questions are all ‘no’, you may be able to reject the paper without reading further than the abstract or introduction.