Read In Pursuit of the Unknown Online
Authors: Ian Stewart
In Pursuit of the Unknown (17 page)
Table 1
The development of algebraic notation.
The most important topics in the
Ars Magna
were new methods for solving cubic and quartic equations. These are like quadratic equations, which most of us meet in school algebra, but more complicated. A quadratic equation states a relationship involving an unknown quantity, normally symbolised by the letter
x
, and its square
x
2
. âQuadratic' comes from the Latin for âsquare'. A typical example is
Verbally, this says: âSquare the unknown, subtract 5 times the unknown, and add 6: the result is zero.' Given an equation involving an unknown, our task is to solve the equation â to find the value or values of the unknown that make the equation correct.
x
2
â 5
x
+ 6 = 0
For a randomly chosen value of
x
, this equation will usually be false. For example, if we try
x
= 1, then
x
2
â 5
x
+ 6 = 1 â 5 + 6 = 2, which isn't zero. But for rare choices of
x
, the equation is true. For example, when
x
= 2 we have
x
2
â5
x
+ 6 = 4 â 10 + 6 = 0. But this is not the
only
solution! When
x
= 3 we have
x
2
â 5
x
+ 6 = 9 â 15 + 6 = 0 as well. There are two solutions,
x
= 2 and
x
= 3, and it can be shown that there are no others. A quadratic equation can have two solutions, one, or none (in real numbers). For example,
x
â 2
x
+ 1 = 0 has only the solution
x
= 1, and
x
2
+ 1 = 0 has no solutions in real numbers.
Cardano's masterwork provides methods for solving cubic equations, which along with
x
and
x
2
also involve the cube
x
3
of the unknown, and quartic equations, where
x
4
turns up as well. The algebra gets very complicated; even with modern symbolism it takes a page or two to derive the answers. Cardano did not go on to quintic equations, involving
x
5
, because he did not know how to solve them. Much later it was proved that no solutions (of the type Cardano would have wanted) exist: although highly accurate numerical solutions can be calculated in any particular case, there is no general
formula
for them, unless you invent new symbols specifically for the task.
I'm going to write down a few algebraic formulas, because I think the topic makes more sense if we don't try to avoid them. You don't need to follow the details, but I'd like to show you what everything looks like. Using modern symbols, we can write out Cardano's solution of the cubic equation in a special case, when
x
3
+
ax
+
b
= 0 for specific numbers
a
and
b
. (If
x
2
is present, a cunning trick gets rid of it, so this case actually deals with everything.) The answer is:
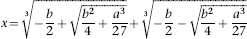
This may appear a bit of a mouthful, but it's a lot simpler than many algebraic formulas. It tells us how to calculate the unknown
x
by working out the square of
b
and the cube of
a
, adding a few fractions, and taking a couple of square roots (the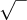 symbol) and a couple of cube roots (the
symbol) and a couple of cube roots (the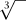 symbol). The cube root of a number is whatever you have to cube to get that number.
symbol). The cube root of a number is whatever you have to cube to get that number.
The discovery of the solution for cubic equations involves at least three other mathematicians, one of whom complained bitterly that Cardano had promised not to reveal his secret. The story, though fascinating, is too complicated to relate here.
1
The quartic was solved by Cardano's student Lodovico Ferrari. I'll spare you the even more complicated formula for quartic equations.
The results reported in the
Ars Magna
were a mathematical triumph, the culmination of a story that spanned millennia. The Babylonians knew how to solve quadratic equations around 1500
BC
, perhaps earlier. The ancient Greeks and Omar Khayyam knew geometric methods for solving cubics, but algebraic solutions of cubic equations, let alone quartics, were unprecedented. At a stroke, mathematics outstripped its classical origins.
There was one tiny snag, however. Cardano noticed it, and several people tried to explain it; they all failed. Sometimes the method works brilliantly; at other times, the formula is as enigmatic as the Delphic oracle. Suppose we apply Cardano's formula to the equation
x
3
â 15
x
â 4 = 0. The result is
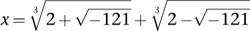
However, â121 is negative, so it has no square root. To compound the mystery, there is a perfectly good solution,
x
= 4. The formula doesn't give it.
Light of a kind was shed in 1572 when Bombelli published
L'Algebra
. His main aim was to clarify Cardano's book, but when he came to this particular thorny issue he spotted something Cardano had missed. If you ignore what the symbols mean, and just perform routine calculations, the standard rules of algebra show that
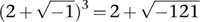
Therefore you are entitled to write
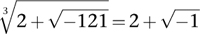
Similarly,
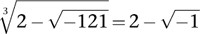
Now the formula that baffled Cardano can be rewritten as
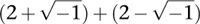
which is equal to 4 because the troublesome square roots cancel out. So Bombelli's nonsensical formal calculations
got the right answer
. And that was a perfectly normal real number.
Somehow, pretending that square roots of negative numbers made sense, even though they obviously did not, could lead to sensible answers. Why?
To answer this question, mathematicians had to develop good ways to think about square roots of negative quantities, and do calculations with them. Early writers, among them Descartes and Newton, interpreted these âimaginary' numbers as a sign that a problem has no solutions. If you wanted to find a number whose square was minus one, the formal solution âsquare root of minus one' was imaginary, so no solution existed. But Bombelli's calculation implied that there was more to imaginaries than that. They could be used to
find
solutions; they could arise as part of the calculation of solutions that
did
exist.