Read In Pursuit of the Unknown Online
Authors: Ian Stewart
In Pursuit of the Unknown (21 page)
In fact, the formula lets us sidestep the tricky issue of defining âhole' altogether. Instead, we define ânumber of holes' as a package, without either defining a hole or counting how many there are. How? Easy. Just rewrite the generalised version of Euler's formula
F
â
E
+
V
= 2 â2
g
in the form
g
= 1 â
F
/2 +
E
/2 â
V
/2
Now we can calculate
g
by drawing faces and so forth on our solid, counting
F, E
, and
V
, and substituting those values into the formula. Since the expression is an invariant, it doesn't matter how we cut the solid up: we always get the same answer. But nothing that we do depends on having a definition of a hole. Instead, ânumber of holes' becomes an interpretation, in intuitive terms, derived by looking at simple examples where we feel we know what the phrase should mean.
It may seem like a cheat, but it makes significant inroads into a central question in topology: when can one shape be continuously deformed into another? That is, as far as topologists are concerned, are the two shapes the same or not? If they are the same, their invariants must also be the same; conversely, if the invariants are different, so are the shapes. (However, sometimes two shapes might have the same invariant, but be different; it depends on the invariant.) Since a sphere has Euler characteristic 2, but a torus has Euler characteristic 0, there is no way to deform a sphere continuously into a torus. This may seem obvious, because of the hole. . . but we've seen the turbulent waters into which that way of thinking can lead. You don't have to interpret the Euler characteristic in order to use it to distinguish shapes, and here it is decisive.
Less obviously, the Euler characteristic shows that the puzzling hole-through-a-hole-in-a-hole (
Figure 24
) is actually just a 3-holed torus in disguise. Most of the apparent complexity stems not from the intrinsic topology of the surface, but from the way I have chosen to embed it in space.
The first really significant theorem in topology grew out of the formula for the Euler characteristic. It was a complete classification of surfaces, curved two-dimensional shapes like the surface of a sphere or that of a torus. A couple of technical conditions were also imposed: the surface should have no boundary, and it should be of finite extent (the jargon is âcompact').
For this purpose a surface is described intrinsically; that is, it is not conceived as existing in some surrounding space. One way to do this is to view the surface as a number of polygonal regions (which topologically are equivalent to circular discs) that are glued together along their edges according to specified rules, like the âglue tab A to tab B' instructions you get when assembling a cardboard cut-out. A sphere, for instance, can be described using two discs, glued together along their boundaries. One disc becomes the northern hemisphere, the other the southern hemisphere. A torus has an especially elegant description as a square with opposite edges glued to each other. This construction can be visualised in a surrounding space (
Figure 25
), which explains why it creates a torus, but the mathematics can be carried out using just the square together with the gluing rules, and this offers advantages precisely because it is intrinsic.
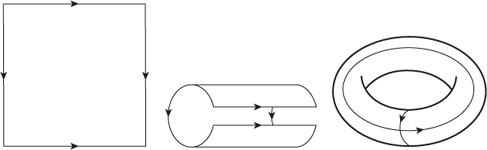
Fig 25
Gluing the edges of a square to make a torus.
The possibility of gluing bits of boundary together leads to a rather strange phenomenon: surfaces with only one side. The most famous example is the Möbius band, introduced by Möbius and Listing in 1858, which is a rectangular strip whose ends are glued together with a 180° turn (usually called a half-twist, on the convention that 360° constitutes a full twist). The Möbius band, see
Figure 26
(
left)
, has an edge, comprising the edges of the rectangle that don't get glued to anything. This is the only edge, because the two separate edges of the rectangle are connected together into a closed loop by the half-twist, which glues them end to end.
It is possible to make a model of a Möbius band from paper, because it embeds naturally in three-dimensional space. The band has only one side, in the sense that if you start painting one of its surfaces, and keep going, you will eventually cover the entire surface, front and back. This happens because the half-twist connects the front to the back. That's not an intrinsic description, because it relies on embedding the band in space, but
there is an equivalent, more technical property known as orientability, which is intrinsic.
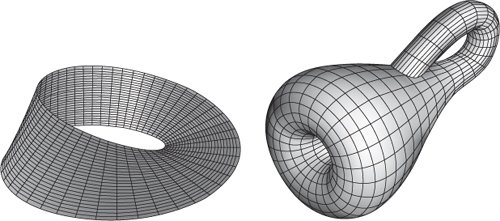
Fig 26
Left
: Möbius band.
Right
: Klein bottle. The apparent self-intersection occurs because the drawing embeds it in three-dimensional space.
There is a related surface with only one side, having no edges at all,
Figure 26
(
right
). It arises if we glue two sides of a rectangle together like a Möbius band, and glue the other two sides together without any twisting. Any model in three-dimensional space has to pass through itself, even though from an intrinsic point of view the gluing rules do not introduce any self-intersections. If this surface is pictured with such a crossing, it looks like a bottle whose neck has been poked through the side wall and joined to the bottom. It was invented by Felix Klein, and is known as a Klein bottle â almost certainly a joke based on a German pun, changing
Kleinsche Fläche
(Klein's surface) to
Kleinsche Flasche
(Klein's bottle).
The Klein bottle has no boundary and is compact, so any classification of surfaces must include it. It is the best known of an entire family of onesided surfaces, and surprisingly it is not the simplest. This honour goes to the projective plane, which arises if you glue both pairs of opposite sides of a square together, with a half-twist for each. (This is difficult to do with paper because paper is too rigid; like the Klein bottle it requires the surface to intersect itself. It is best done âconceptually', that is, by drawing pictures on the square but remembering the gluing rules when lines go off the edge and âwrap round'.) The classification theorem for surfaces, proved by Johann Listing around 1860, leads to two families of surfaces. Those with two sides are the sphere, torus, 2-holed torus, 3-holed torus, and so on. Those with only one side form a similar infinite family, starting with the projective plane and the Klein bottle. They can be obtained by cutting a
small disc out of the corresponding two-sided surface and gluing in a Möbius band instead.
Surfaces turn up naturally in many areas of mathematics. They are important in complex analysis, where surfaces are associated with singularities, points at which functions behave strangely â for instance, the derivative fails to exist. Singularities are the key to many problems in complex analysis; in a sense they capture the essence of the function. Since singularities are associated with surfaces, the topology of surfaces provides an important technique for complex analysis. Historically, this motivated the classification.
Most modern topology is highly abstract, and a lot of it happens in four or more dimensions. We can get a feel for the subject in a more familiar setting: knots. In the real world, a knot is a tangle tied in a length of string. Topologists need a way to stop the knot escaping off the ends once it has been tied, so they join the ends of the string together to form a closed loop. Now a knot is just a circle embedded in space. Intrinsically, a knot is topologically identical to a circle, but on this occasion what counts is how the circle sits inside its surrounding space. This might seem contrary to the spirit of topology, but the essence of a knot lies in the relation between the loop of string and the space that surrounds it. By considering not just the loop, but how it relates to space, topology can tackle important questions about knots. Among these are:
â¢
How do we know a knot is really knotted?
â¢
How can we distinguish topologically different knots?
â¢
Can we classify all possible knots?
Experience tells us that there are many different types of knot.
Figure 27
shows a few of them: the overhand or trefoil knot, reef knot, granny knot, figure-8, stevedore's knot, and so on. There is also the unknot, an ordinary circular loop; as the name reflects, this loop is
not
knotted. Many different kinds of knot have been used by generations of mariners, mountaineers, and boy scouts. Any topological theory should of course reflect this wealth of experience, but everything has to be proved, rigorously, within the formal setting of topology, just as Euclid had to prove Pythagoras's theorem instead of just drawing a few triangles and measuring them. Remarkably, the first topological proof that knots exist, in the sense that there is an embedding of the circle that cannot be deformed into the unknot, first appeared in 1926 in the German mathematician Kurt Reidemeister's
Knoten und Gruppen
(âKnots and Groups'). The word âgroup' is a technical term in abstract algebra, which quickly became the most effective source of topological invariants. In 1927 Reidemeister, and independently the American James Waddell Alexander, in collaboration with his student G. B. Briggs, found a simpler proof of the existence of knots using the âknot diagram'. This is a cartoon image of the knot, drawn with tiny breaks in the loop to show how the separate strands overlap, as in
Figure 27
. The breaks are not present in the knotted loop itself, but they represent its three-dimensional structure in a two-dimensional diagram. Now we can use the breaks to split the knot diagram into a number of distinct pieces, its components, and then we can manipulate the diagram and see what happens to the components.
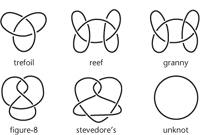
Fig 27
Five knots and the unknot.
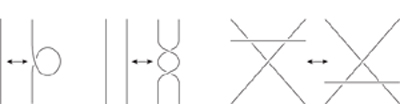
If you look back at how I used the invariance of the Euler characteristic, you'll see that I simplified the solid using a series of special moves: merge two faces by removing an edge, merge two edges by removing a point. The same trick applies to knot diagrams, but now you need three types of move to simplify them, called Reidemeister moves,
Figure 28
. Each move can be carried out in either direction: add or remove a twist, overlap two strands or pull them apart, move one strand through the place where two others cross.