In Pursuit of the Unknown (44 page)

d
²
= (
x
–
X
)
²
+ (
y
–
Y
)
²
+(
z
–
Z
)
²
–
c
²
(
t
–
T
)
²

The factor
c
²
is just a consequence of the units used to measure time, but the minus sign in front of it is crucial. The ‘distance'
d
is called the interval, and the square root is real only when the right-hand side of the equation is positive. That boils down to the spatial distance between the two events being larger than the temporal difference (in correct units: light-years and years, for instance). That in turn means that in principle a body could travel from the first point in space at the first time, and arrive at the second point in space at the second time, without going faster than light.

In other words, the interval is real if and only if it is physically possible, in principle, to travel between the two events. The interval is zero if and only if light could travel between them. This physically accessible region is called the light cone of an event, and it comes in two pieces: the past and the future.
Figure 50
shows the geometry when space is reduced to one dimension.

I've now shown you three relativistic equations, and sketched how they arose, but none of them is Einstein's iconic equation. However, we're now ready to understand how he derived it, once we appreciate one more innovation of early twentieth-century physics. As we've seen, physicists had previously performed experiments to demonstrate conclusively that light is a wave, and Maxwell had shown that it is a wave of electromagnetism. However, by 1905 it was becoming clear that despite the weight of evidence for the wave nature of light, there are circumstances in which it behaves like a particle. In that year Einstein used this idea to explain some features of the photoelectric effect, in which light that hits a suitable metal generates electricity. He argued that the experiments made sense only if light comes in discrete packages: in effect, particles. They are now called photons.

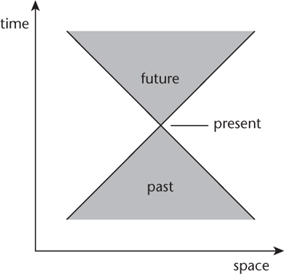
Fig 50
Minkowski space-time, with space shown as one-dimensional.

This puzzling discovery was one of the key steps towards quantum mechanics, and I'll say more about it in
Chapter 14
. Curiously, this quintessentially quantum-mechanical idea was vital to Einstein's formulation of relativity. To derive his equation relating mass to energy, Einstein thought about what happens to a body that emits a pair of photons. To simplify the calculations he restricted attention to one dimension of space, so that the body moved along a straight line. This simplification does not affect the answer. The basic idea is to consider the system in two different frames of reference.
²
One moves with the body, so that the body appears to be stationary within that frame. The other frame moves with a small, nonzero velocity relative to the body. Let me call these the stationary and moving frames. They are like the spaceship (in its own frame of reference it is stationary) and my ground observer (to whom it appears to be moving).

Einstein assumed that the two photons are equally energetic, but emitted in opposite directions. Their velocities are equal and opposite, so the velocity of the body (in either frame) does not change when the photons are emitted. Then he calculated the energy of the system before the body emits the pair of photons, and afterwards. By assuming that energy must be conserved, he obtained an expression that relates the change in the body's energy, caused by emitting the photons, to the change in its (relativistic) mass. The upshot was:

(change in energy) = (change in mass) ×
c
²

Making the reasonable assumption that a body of zero mass has zero energy, it then followed that

energy = mass ×
c
²

This, of course, is the famous formula, in which
E
symbolises energy and
m
mass.

As well as doing the calculations, Einstein had to interpret their meaning. In particular, he argued that in a frame for which the body is at rest, the energy given by the formula should be considered to be its ‘internal' energy, which it possesses because it is made from subatomic particles, each of which has its own energy. In a moving frame, there is also a contribution from kinetic energy. There are other mathematical subtleties too, such as the use of a small velocity and approximations to the exact formulas.

Einstein is often credited, if that's the word, with the realisation that an atomic bomb would release stupendous quantities of energy. Certainly
Time
magazine gave that impression in July 1946 when it put his face on the cover with an atomic mushroom cloud in the background bearing his iconic equation. The connection between the equation and a huge explosion seems clear: the equation tells us that the energy inherent in any object is its mass multiplied by the square of the speed of light. Since the speed of light is huge, its square is even bigger, which equates to a lot of energy in a small amount of matter. The energy in one gram of matter turns out to be 90 terajoules, equivalent to about one day's output of electricity from a nuclear power station.

However, it didn't happen like that. The energy released in an atomic bomb is only a tiny fraction of the relativistic rest mass, and physicists were already aware, on experimental grounds, that certain nuclear reactions could release a lot of energy. The main technical problem was to hold a lump of suitable radioactive material together long enough to get a chain reaction, in which the decay of one radioactive atom causes it to emit radiation that triggers the same effect in other atoms, growing exponentially. Nevertheless, Einstein's equation quickly became established in the public mind as the progenitor of the atomic bomb. The Smyth report, an American government document released to the public to explain the atomic bomb, placed the equation on its second page. I suspect that what happened is what Jack Cohen and I have called ‘lies to
children' – simplified stories told for legitimate purposes, which pave the way to more accurate enlightenment.
³
This is how education works: the full story is always too complicated for anyone except the experts, and they know so much that they don't believe most of it.

However, Einstein's equation can't just be dismissed out of hand. It did play a role in the development of nuclear weapons. The notion of nuclear fission, which powers the atom bomb, arose from discussions between the physicists Lise Meitner and Otto Frisch in Nazi Germany in 1938. They were trying to understand the forces that held the atom together, which were a bit like the surface tension of a drop of liquid. They were out walking, discussing physics, and they applied Einstein's equation to work out whether fission was possible on energy grounds. Frisch later wrote:
⁴

We both sat down on a tree trunk and started to calculate on scraps of paper. . . When the two drops separated they would be driven apart by electrical repulsion, about 200 MeV in all. Fortunately Lise Meitner remembered how to compute the masses of nuclei. . . and worked out that the two nuclei formed. . . would be lighter by about one-fifth the mass of a proton. . . according to Einstein's formula
E
=
mc
²
. . . the mass was just equivalent to 200 MeV. It all fitted!

Although
E
=
mc
²
was not directly responsible for the atom bomb, it was one of the big discoveries in physics that led to an effective theoretical understanding of nuclear reactions. Einstein's most important role regarding the atomic bomb was political. Urged by Leo Szilard, Einstein wrote to President Roosevelt, warning that the Nazis might be developing atomic weapons and explaining their awesome power. His reputation and influence were enormous, and the president heeded the warning. The Manhattan Project, Hiroshima and Nagasaki, and the ensuing Cold War were just some of the consequences.

Einstein wasn't satisfied with special relativity. It provided a unified theory of space, time, matter, and electromagnetism, but it missed out one vital ingredient.

Gravity.

Einstein believed that ‘all the laws of physics' must satisfy his extended version of Galileo's principle of relativity. The law of gravitation surely ought to be among them. But that wasn't the case for the current version of relativity. Newton's inverse square law did not transform correctly between
frames of reference. So Einstein decided he had to change Newton's law. He'd already changed virtually everything else in the Newtonian universe, so why not?

It took him ten years. His starting-point was to work out the implications of the principle of relativity for an observer moving freely under the influence of gravity – in a lift that is dropping freely, for example. Eventually he homed in on a suitable formulation. In this he was aided by a close friend, the mathematician Marcel Grossmann, who pointed him towards a rapidly growing field of mathematics: differential geometry. This had developed from Riemann's concept of a manifold and his characterisation of curvature, discussed in
Chapter 1
. There I mentioned that Riemann's metric can be written as a 3 × 3 matrix, and that technically this is a symmetric tensor. A school of Italian mathematicians, notably Tullio Levi-Civita and Gregorio Ricci-Curbastro, took up Riemann's ideas and developed them into tensor calculus.

From 1912, Einstein was convinced that the key to a relativistic theory of gravity required him to reformulate his ideas using tensor calculus, but in a 4-dimensional space-time rather than 3-dimensional space. The mathematicians were happily following Riemann and allowing any number of dimensions, so they had already set things up in more than enough generality. To cut a long story short, he eventually derived what we now call the Einstein field equations, which he wrote as:

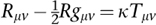
Here
R, g
, and
T
are tensors – quantities that define physical properties and transform according to the rules of differential geometry – and
κ
is a constant. The subscripts
μ
and
v
run over the four coordinates of space-time, so each tensor is a 4 × 4 table of 16 numbers. Both are symmetric, meaning that they don't change when
μ
and
v
are swapped, which reduces them to a list of 10 distinct numbers. So really the formula packages together 10 equations, which is why we often refer to them using the plural – compare Maxwell's equations.
R
is Riemann's metric: it defines the shape of space-time.
g
is the Ricci curvature tensor, which is a modification of Riemann's notion of curvature. And
T
is the energy–momentum tensor, which describes how these two fundamental quantities depend on the space-time event concerned. Einstein presented his equations to the Prussian Academy of Science in 1915. He called his new work the general theory of relativity.

We can interpret Einstein's equations geometrically, and when we do,
they provide a new approach to gravity. The basic innovation is that gravity is not represented as a force, but as the curvature of space-time. In the absence of gravity, space-time reduces to Minkowski space. The formula for the interval determines the corresponding curvature tensor. Its interpretation is ‘not curved', just as Pythagoras's theorem applies to a flat plane but not to a positively or negatively curved non-Euclidean space. Minkowski space-time is flat. But when gravity occurs, space-time
bends
.