Mathematics and the Real World (20 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein
This explanation is very general, and in 1740 the French Royal Academy of Sciences offered a prize to anyone who would develop an exact detailed mathematical explanation. Such developments, based on
Newton's laws, were offered, separately, by Daniel Bernoulli, Leonhard Euler, Colin Maclaurin, and Antonine Cavalleri, all of whom were (jointly) awarded the prize. Sufficient numerical calculations describing the ebb and flow of the tides around the whole world were achieved only in the 1950s, at the Weizmann Institute of Science in Israel, with the appearance of electronic computers.
The mathematical formula that describes Newton's law of gravity omits one important link, and that is the question of the mechanism through which the attraction operates. Since Aristotle, the idea had become deeply entrenched that matter is continuous and that was what enabled force to be exerted by one body on another. Aristotle's opposition to the atomistic approach was based on, among other things, his puzzlement about how a force could be exerted despite the vacuum between the atoms. Newton's law of gravity gives a mathematical formula for the size of the force but does not refer to how the force is exerted. Newton did not ignore this question, and to answer it he adopted Aristotle's solution to the movement of heavenly bodies, taken up by Ptolemy, of the existence of the ether, that imperceptible material that fills the whole world. The great success of Newton's formula in predicting events and foreseeing orbits diverted research from studying what the ether was and trying to prove its existence.
Newton's contributions to science and mathematics far exceeded what we have described briefly above. They included fundamental contributions to optics, including the separation of white light into the colors of the spectrum, and in mathematics, for example, his binomial law, and so on. His great conceptual innovation in mathematics and science derived from his daring to create a new mathematics, specifically to describe phenomena in nature. After Newton, mathematicians did not hesitate to develop new branches of mathematics to describe nature better.
21. PURPOSE: THE PRINCIPLE OF LEAST ACTION
In his laws, Newton ignored the purpose that Aristotle's approach required. He made do with formulating mathematical laws through which, using mathematical operations, properties of the element being studied could be derived and predicted. A comparison of the prediction with the actual outcome is what corroborates a mathematical law of nature. When Newton was asked why his laws were formulated as they were, he answered that there was no doubt that God created a world that followed clear and simple mathematical laws. Tradition, however, and the approach that predominated in science until then were deep-rooted enough to make other scientists try to describe natural occurrences via basic principles rather than mere equations.
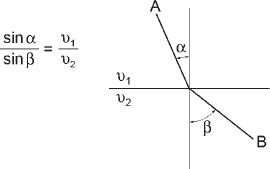
One route followed in the search for a purpose derived from an empirical law. Scientists had long known that the path of a beam of light passing from one medium to another is refracted at the point of transition. Willebrord van Roijen Snell (1580–1626), a Dutch physicist, discovered empirically and formulated what is known today as Snell's law of refraction. The law states that the sines of the angles of refraction are in the same ratio to each other as are the speeds of light in the different media (see the diagram below, in which the speeds of light in the two media are notated
v
1
and
v
2
). The great French mathematician Pierre de Fermat (1601–1665) showed that Snell's law was equivalent to saying that the light beam passes from one point to another in a space such that it minimizes the time to get there. In other words, if we choose two points, A and B, on the beam, the point of refraction will be that which reduces the time the light takes to get from A to B to its minimum.
One way of interpreting Fermat's principle is to say that the light beam in effect solves a mathematical problem: it chooses a route that will get it as quickly as possible from one point to another. Fermat proved that the solution to the mathematical problem was given by Snell's formula. Obviously neither Fermat nor his successors claimed that the light beam had the purpose of reaching its destination as quickly as possible. They saw this property as a basic principle beyond a mathematical description, and thus, in the Greek tradition, the principle of the least time served as the purpose underlying the law of nature.
It is interesting to note that the Greeks themselves used a similar rationale. As is generally known, the angle of reflection of a beam of light striking a mirror equals the angle at which it strikes the mirror (or the angle of incidence equals the angle of reflection). Hero (or Heron) of Alexandria (10–70 CE) proved that the identity of the two angles leads to the conclusion that a beam of light from point A toward a mirror is reflected by the mirror and reaches a point B such that it moves from A to B (via the mirror) in the shortest possible time. Hero's reasoning, however, was inverted by Fermat. Hero considered it axiomatic that the angle of incidence equals the angle of reflection and proved that the light took the quickest route. Fermat proposed as an axiom, as a purpose, the principle of the minimum time and concluded that, in the case of the beam reflected from a mirror, the angles had to be equal.
From the time Newton's laws were published, many scientists tried to generalize Fermat's least time principle so that it would also apply to new laws. The most famous of those scientists were Leibniz, Euler, Lagrange, and Hamilton. The modern formulation of this type of principle, that is, the least action principle, is attributed to the latter. In this, the purpose is achieved by minimizing the integral along the path the body takes, integral of the physical quantity called the momentum of the system, that is, the multiple of the mass and the speed. This principle too is corroborated by experiments. Moreover, Newton's equations of motion can be derived from this principle. Hence, at least as far as mechanics are concerned, complete equivalence has been achieved between the direct mathematical description of the equations of motion and the description of the system
by means of the purpose inherent in the least action principle. The reason for nature revealing such “efficiency” is a question with no clear answer.
Moreover, sometimes we try to attribute to nature an element of efficiency that it apparently does not have. For example, parts of lava fields have hardened into hexagonal shapes, as can be seen in the photograph below, taken in Iceland. The explanation offered by the tour guide and by scientists I have asked about this is that covering an area with hexagons is a solution to the minimum energy problem, which is rather difficult to formulate. The hexagonal structure of honeycombs is explained in a similar fashion. The bees try to “solve” the problem of constructing a surface of cells of a given magnitude with minimum length of walls. The intention is to minimize the amount of wax required. The ancient Greeks already conjectured that hexagons offer a solution to this minimization problem, called the honeycomb conjecture. Many tried to resolve the issue, but a complete proof of this mathematical fact was published in only 2001 by Thomas C. Hales of the University of Michigan, more recently of the University of Pittsburgh.
In regard to lava hexagons, I offer an alternative explanation. The support offered by one hexagon to its neighbors makes the hexagonal structure the most stable, the most able to withstand external forces of displacement. At the time of the formation of the lava fields, various weird and wonderful
shapes were formed, covering different areas, such as squares and triangles. Those small areas covered by hexagons best survived the shocks and earthquakes that occurred there, which is why that is the shape we can see today, millions of years after its formation. That is also why the area covered by hexagons is only a small part of the total lava fields, with only smaller areas covered by other shapes that survived too. With regard to honeycombs, evolution may have taught bees to solve the honeycomb problem, but it may also be the case that the stability aspect also played a role; in other words, evolution selected the bees that constructed stabler honeycombs.
22. THE WAVE EQUATION
The laws of nature set out in the form of the relation between functions and their rates of change, that is, using differential equations, have, since Newton, become the major instrument used to understand nature through mathematics. Newton laid the foundation, and from his days until today scientists use his method and propose new equations to describe additional natural phenomena. If and when the experimental results corroborate the correctness of the equation, it is customary to name the equation after the scientist who proposed it. The following is a partial list of equations mentioned in the titles of lectures given recently in mathematical conferences in which I participated: Euler equation, Riccati equation, Navier-Stokes equation, Korteweg-de Vries equation, Burgers equation, Smoluchowski equation, Euler-Lagrange equation, Lyapunov equation, Bellman equation, Hamilton-Jacobi equation, Lotka-Volterra equation, Schrödinger equation, Kuramoto-Sivashinsky equation, Cucker-Smale equation, and so on. Each equation has its story and its use. Generally, the equations are formulated in terms of the relation between a function or a set of functions and their derivatives or integrals. The equations implement Newton's laws, sometimes in conjunction with other laws of nature, such as the law of conservation of energy or the law of conservation of matter. The names of the equations show that scientists have been using differential equations since Newton and continue to do so, and much remains to be done.
In this section we will present one equation that connects the distant past with the current era. This equation played a crucial role in the additional revolution in the relation between mathematics and nature, a revolution that we will discuss in the
next chapter
. The equation is not named after its formulator but after what it describes, namely, the wave equation. We are particularly interested in one specific aspect of it, and that is the string equation. No mathematical background is needed to understand what follows, but it does call for patience and tolerance for the mathematical symbols (and these can also be skipped without impairing the understanding of the text).
Undulations, or wavelike motion, can be seen in many of the materials around us, from the actual waves in the sea to the vibrations of string or membranes stretched to different extents. As we stated in the previous section, the equation that describes the motion of a spring or a pendulum was put forward as early as in Newton's days. In discussing the oscillation of a stretched piece of string or the movement of the waves in the sea, the situation is slightly more complex as the height of the wave changes from one place to another, and it also changes with time. That is, to describe a wave requires a function of time and place. The height of the wave may be notated by
u
, and for every location
x
and time
t
, the quantity
u
(
x
,
t
) will represent the height of the wave at that location and at that time. We can relate to the rate of change of the height of the wave according to the time at a fixed location, and according to the location at a fixed point in time. The rate of change of the function according to location at a fixed time (imagine the profile of a wave at a given moment in time) is written in mathematics as ∂
x
u
(
x
,
t
), and it is called the
partial derivative
by location (the notation ∂ was introduced to mathematics by the Marquis de Condorcet in 1770; some attribute it to the mathematician Adrien-Marie Legendre in 1786). Similarly, the expression ∂
t
u
(
x
,
t
) indicates the rate of change of the function according to time (imagine the increase and decrease in the height of the wave at a given location). The second derivatives, that is to say the rate of change of the function of the rate of change, are written in mathematics as ∂
xx
u
(
x
,
t
), and ∂
tt
u
(
x
,
t
), respectively (see the diagram below of an advancing wave). The height of the wave varies with time and location. The law of its change will be given by a differential equation.