Mathematics and the Real World (34 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein
Now we ask a more complex question. A coin is removed from a box that was chosen randomly, and it turns out to be a gold coin. What are the chances that the coin left in the box is silver? It is simple to formulate the question, but try giving an intuitive answer (without having to use formulae that you may have learned in lessons on probability). A simple analysis shows that from the information that a gold coin was taken from the box we can conclude that the box chosen was not the first (which held two silver coins). The other two boxes have an equal chance of being selected, that is, 50 percent. If the second box is chosen, the remaining coin will be the silver one (as the gold coin was taken out). If the third box is selected, the remaining coin will be the second gold one in that box. Thus, in the situation as described with a gold coin removed from a randomly selected box, the probability of the remaining coin being silver is one-half. Although this analysis is simple, it is incorrect (there was a reason that de Moivre did not arrive at a satisfactory answer to the question of how to solve such problems and left it in his book as an open question). The error is similar to the one committed by Pascal in his first letter to Fermat, as described in a previous section. In other words, the “solution” ignores the probabilities of a gold coin being selected in the different scenarios and therefore is in error in the precise implication it draws from the information. The correct analysis is: the gold coin that was drawn from the selected box came either from the second box (with a gold and a silver coin) with a probability of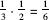 , or from the third box (which held two gold coins) with a probability of
, or from the third box (which held two gold coins) with a probability of . Only in the first of these two possibilities will the remaining coin be silver. The weight of that happening in the number of occurrences in which a gold coin is selected in the first draw is
. Only in the first of these two possibilities will the remaining coin be silver. The weight of that happening in the number of occurrences in which a gold coin is selected in the first draw is divided by
divided by , that is, one-third.
, that is, one-third.
The principle underlying the above calculation is simple. If you wish to draw a conclusion based on new information, you have to take into account all the factors that are likely to result in that information reaching you, and to weight all those factors according to their probabilities. Specifically, relating to our above example, assume that you want to find the probability that event
B
will occur, given that you are told that
A
has occurred.
First, find the chance that you will be told that
A
has occurred if
B
occurs. Then find the chance that you will be told that
A
occurred if
B
does not occur. Then calculate the weight of being told that
A
occurred if
B
occurred relative to the total chance of being told that
A
occurred. This scheme can be written in the form of a formula, which we will set out in the next section. The principle underlying the weighting is the essence of the Bayes's scheme. We will present several other examples that will make the situation even clearer.
The principle presented by Bayes enables the probabilities to be updated whenever new information is received. Theoretically the probabilities could be updated continuously until exact assessments are obtained. That refinement of Bayes's scheme was developed by Laplace. Laplace apparently arrived independently at a formula similar to Bayes's and then developed the complete formulae of updates that become more and more exact, but when he heard of Bayes's previous work, he gave Bayes's name to the method. That name, the Bayesian inference or Bayesian statistics, has prevailed still today.
But the approach has a fundamental drawback. In order to apply Bayes's formula we need to know the probabilities that the events we are referring to will take place. The problem is that generally, in our daily lives, the information regarding these probabilities is not known. How then can we learn from experience? Bayes had a controversial answer: if you have no idea of the probability that
A
will occur or will not occur, assume that the chances are equal. Once you assume the initial probabilities, also called the a priori probabilities, you can calculate the new probability, called the a posteriori probability, with a high degree of accuracy. The question arises: Can we allow the use of an arbitrary assumption about the values of an a priori probability?
The dispute between the supporters and the opponents of the system was not limited by space or time. The statistics of frequencies and samples had a firm theoretical basis, but to use it required very many repetitions of the same random occurrence. This type of statistics was not applicable to statistical assessments of non-repeated events. Bayesian statistics is a tool
for analyzing isolated events, but without reliable information on a priori probabilities, the results depend on subjective assessments, and these do not constitute a reliable basis for scientific findings, its opponents claimed. It is better to rely on subjective assessments than to ignore the advantages offered by the method, replied its supporters. Moreover, they added, the more information that is added, the greater the reduction in the effect of the arbitrary assumptions, until it reaches a minimum, a fact that gives scientific validity to the Bayesian approach. This dispute spilled over onto a personal level, and for many years the two methods developed side by side. Even today statisticians are divided into Bayesians and non-Bayesians, but it now seems that the borders and limitations of the two methods have been drawn more clearly, and each occupies its proper position.
41. THE FORMALISM OF PROBABILITY
The mathematical developments and increasing uses of the concepts of probability theory and statistical methods resulted in the accumulation of great expertise in the practice of the mathematical theory at the beginning of the twentieth century. This development, however, was accompanied by much unease, the roots of which were mentioned previously. First, there was the duality in the subject matter. The same terms and considerations were used both in the analysis of repeated events, in which the probability can be interpreted as the proportion of total occurrences in which the event takes place, as well as in cases of assessing the probability of a non-repeated event. Second, no understanding or agreement had been reached regarding the source of the probabilities. Even in coin-flipping experiments, the only reason for thinking that both sides of the coin had equal chances of falling uppermost was that there was no reason for thinking that the chances were not equal. Is that argument strong enough to convince us that the calculations represent nature? In addition, there was no general logical mathematical framework for dealing with the mathematics of randomness. For example, no one had proposed a precise general definition of the concept of independence. The reader will no doubt have noticed that
we have used the term
independent
several times, and the intuitive feeling is that even without a formal definition, we know when events are independent. That feeling, however, is not enough for mathematical analysis, and a definition that met the strict criteria of mathematics did not exist.
George Boole (1815–1864), a British mathematician and philosopher, tried to present a general mathematical framework. He claimed that mathematical logic, and in particular the union and intersection of sets to present information, is appropriate for the analysis of events involving probabilities. To this end Boole constructed the basis of logic through the use of sets and defined what is today known as Boolean algebra. These efforts did not result in much success, however, among other reasons because Boole's works contained discrepancies that resulted from a lack of consistency in the model he used. For example, Boole related in different and conflicting ways to the concept of independence. In one case independence meant the inability to imply a conclusion from one event to another, and in another case it meant that events do not overlap. Thus, at the beginning of the twentieth century, the mathematics of randomness did not provide a satisfactory answer regarding how to analyze events involving probabilities and the sources from which those probabilities originated.
It was Andrey Kolmogorov (1903–1987) who proposed the complete framework of logic. Kolmogorov was a preeminent mathematician of the twentieth century. In addition to his contribution to mathematical research, he was interested in the teaching of mathematics in schools and held various administrative positions in universities and Russian academia. Kolmogorov made important contributions in a wide range of mathematical subjects: Fourier series, set theory, logic, fluid mechanics, turbulence, analysis of complexity, and probability theory, which we will turn to shortly. He was granted many awards and honors, including the Stalin Prize, the Lenin Prize, and, in 1980, the prestigious Wolf Prize, the award ceremony of which he did not attend. This led to a change in the rules of the prize, so that in order to be awarded the prize, the recipient must attend the ceremony.
Kolmogorov adopted the Greeks’ approach. He drew up a list of
axioms with which the concepts that had previously been used only intuitively could be explained. We will discuss the connection between the axioms and nature after we have presented them. Kolmogorov's general approach adopted George Boole's proposal from several decades earlier, that is, the use of logic operators on sets to describe probabilities. The axioms that Kolmogorov wrote in his book in 1933 are quite simple and are set out below (they can be followed even without previous mathematical knowledge, but even if they are skipped, the text that follows can still be understood).
