The Amazing Story of Quantum Mechanics (14 page)
Read The Amazing Story of Quantum Mechanics Online
Authors: James Kakalios

An understanding of average values and standard deviations of bell-shaped curves is also relevant to issues of climate change and explains why scientists are concerned about an increase in the average global temperature of a few degrees, which admittedly does not sound that menacing.
Consider a histogram plot of the temperature of North America, where the horizontal axis lists the average daily temperature, and the vertical axis charts the number of days per year for which that particular average temperature is recorded. We expect to find, and we do, a roughly bell-shaped curve, just as we have been discussing for grades in a large class or measurements of an electron’s position or momentum. There will be a large peak in the temperature histogram around the average daily temperature over the course of a year, and small tails at lower and higher temperatures.
What is the effect of the yearly average temperature being raised by a few degrees? The answer is easiest to see if we briefly return to the classroom analogy. Suppose we add 5 extra-credit points to every student’s final exam paper. Thus, if the average had been a grade of 50 before, now it will be 55, and the lowest score will shift from 0 to 5, while the highest possible grade will move from 100 to 105. A shift in the average grade from 50 to 55 does not seem like much, and for most students there will be no significant effect. I am just adding a uniform 5 points to everyone’s grade, so the shape of the curve does not change. In addition, I do not adjust the cutoff line for what grade merits an A, what score deserves a B, and so on. In this case I would find that by shifting the grades upward by only 5 points, the number of students that are at or above the A-cutoff threshold has increased dramatically. A minor shift in the average, which does not have a large influence on the grade of the majority of the students, has a big impact on those students that were near but just below the threshold for a letter grade of A.
A small shift in the average annual global temperature is akin to giving everyone in the class 5 extra-credit points. There will thus be more days with higher-than-normal average temperatures (corresponding to those students whose exam performance warranted an A), and those days are what drive extreme weather situations. A shift of the average upward by a few degrees is not a big deal on an average day and is even welcome in the winter in states such as Minnesota, where we would not have such extreme cold snaps. But other parts of the nation in the summer would see a greater number of days where it is hotter than normal. It takes a lot of energy to warm up a large mass of water such as the Gulf of Mexico, and it also takes a long time to cool it back down. The energy of these hotter-than-normal days can be viewed as “stored” in the ocean, and warmer water temperatures can provide energy for hurricanes, tropical storms, and other extreme events. Moreover, the more days with higher temperatures, the more ice will melt in northern regions. Fresh snow reflects 80 to 90 percent of all sunlight shining on it, while liquid water absorbs (and stores) 70 percent of the sunlight. There is thus a positive feedback mechanism by which higher temperatures lead to additional warming. Just as in the case of the Heisenberg uncertainty principle, it’s not the averages that matter so much as the width of the standard deviations. Those long tails will get us in the end.
28
28
CHAPTER EIGHT
Why So Blue, Dr. Manhattan?
In Chapter 5 I stated that
at least some of the amazing superpowers displayed by Dr. Manhattan in the graphic novel and motion picture
Watchmen
are a consequence of his having control over his quantum mechanical wave function. Now that we know a little bit more about wave functions, let’s see how that might work.
at least some of the amazing superpowers displayed by Dr. Manhattan in the graphic novel and motion picture
Watchmen
are a consequence of his having control over his quantum mechanical wave function. Now that we know a little bit more about wave functions, let’s see how that might work.
While it is certainly true that all objects, from electrons, atoms, and molecules to baseballs and research scientists, have a quantum mechanical wave function, one can safely ignore the existence of a matter-wave for anything larger than an atom. This is because the larger the mass, the larger the momentum—and the bigger the momentum, the smaller the spatial extent of the wave function. Anything bigger than an atom or a small molecule has such a large mass that its corresponding de Broglie wavelength is too small to ever be detected. So, right off the bat we must grant Dr. Manhattan a miracle exception from the laws of nature such that he can control his wave function’s spatial extent independently of his momentum. While the de Broglie wavelength for an adult male is typically less than a trillionth trillionth of the width of an atom, Dr. Manhattan must be able to vary his wave function so that it extends a great distance from his body—even as far as the distance between the Earth and Mars!
The quantum mechanical wave function contains all the information about an object. If we want to know the object’s average position, its average speed, its energy, its angular momentum for rotation about a given axis, and how these quantities will change with time, we perform various mathematical operations on the wave function, which yield calculated values for any measured characteristic of the object.
The “wave function” is so named because it is a mathematical function that has the properties of an actual wave. To review: In mathematics a “function” describes any situation where providing one input value leads to the calculation of a related number. The simple equation relating distance to time spent driving at a constant speed—that is, distance = speed × time—is a mathematical function. If your speed is 60 miles per hour, and if you tell me the time you spent driving—1/2 hour, 1 hour, 3 hours—then this simple function enables me to calculate the distance you have covered (30 miles, 60 miles, or 180 miles, respectively, in this example). Most mathematical functions are more complicated than this, and sometimes they get as involved as the Schrödinger wave function, but they all relate some input parameter or parameters to an output value. For the quantum mechanical wave function of an electron in an atom, if you tell me its location in three-dimensional space relative to the nucleus, then the solution to the Schrödinger equation returns the amplitude of the electron’s wave function at that point in space and time.
What does it mean to say that the wave function has the properties of a wave, such as a vibrating string or the series of concentric circles created on the surface of a pond when a rock is tossed into the water? Waves are distinguished by having amplitudes that vary periodically in space and time. Consider the ripples created when a rock is tossed into a pond. At some points of the wave there are crests, where the height of the water wave is large and positive (that is, the surface of the water is higher than normal); at some points there are troughs, where the height of the water is lower than normal; and in other regions the amplitude of the wave is zero—the height of the water’s surface is the same as it would be without the rock’s disturbance.
The amplitude of the peaks and valleys typically becomes smaller with distance from the source of the waves. This is why on the California shore we don’t notice if a rock is dropped into the center of the Pacific Ocean. Certain large disturbances can create tsunamis that maintain large amplitudes even when traveling great distances. Dr. Manhattan, presumably, is able to change the amplitude of his quantum mechanical wave function so that it can have an appreciable amplitude at some large distance away from him. This would be how he teleports, though in quantum mechanics we would say that he is “tunneling.”
Schrödinger’s equation enables us to calculate the wave function of an object as a function of the forces acting on it. If there are no net forces, the electron, for example, can have uniform straight-line motion, with a well-defined de Broglie wavelength determined by its momentum. If this electron strikes a barrier and it lacks sufficient energy to go over the obstacle, then the electron will be reflected, bouncing off the barrier and returning from where it came.
We are familiar with such wave phenomena whenever we use a mirror. Light waves move in straight lines, passing through the glass covering of the mirror, until they reach the silvered backing. Unable to penetrate the metal, the waves are reflected back in another straight-line trajectory, along a path that makes the same angle with a line perpendicular to the mirror’s surface as the incoming beam.
In fact, one does not need the metal backing to see this reflection effect. We all know that a single pane of glass can act like a mirror, when we look out the window from a well-lit room at night. In this case just the difference in optical media, glass and air, can cause light reflection, particularly when we look at the window at an angle. The reflection is more noticeable if the direction we are looking, relative to the glass surface, is larger than a particular angle that depends on the optical properties of glass and air. When we place our face against the glass, this reflection effect goes away, for then most of the light rays that we see from outside travel perpendicular to the surface. Light travels slower in glass than in air (more on this in a moment), and this difference in light velocities (characterized by the material’s index of refraction, for technical reasons) accounts for the reflection effect. This can occur during daytime as well but is less noticeable when more light comes into the room from the outside than goes out from the interior.
Suppose that we are looking at the window at night from the interior of a strongly lit room. The glass reflects our image as if it were a conventional mirror. Now imagine a second sheet of glass placed behind the first, as in a double-paned window, only the separation between the two sheets isn’t a quarter of an inch, but more like a millionth of a centimeter. In this case, even though the light would have been completely reflected without the second sheet of glass, the presence of the second pane enables some of the light to pass through both sheets of glass, even though they are not touching each other. This phenomenon is a hallmark of the wavelike properties of light (so for the sake of argument we will ignore for the moment that light is actually comprised of discrete photons). It turns out that the light wave is not completely reflected at the first glass-air interface, but instead a small amount of the oscillating electric and magnetic fields leak out into the air. The small leakage is limited to a thin region very near the interface and is normally not important. But when the second sheet of glass is brought very close to the first interface, some of the protruding light waves extend into the second piece of glass. In this case the wave is not reflected but rather propagates into the second glass. This “leakage effect” is not unique to light; it occurs for any wave—even those associated with matter!
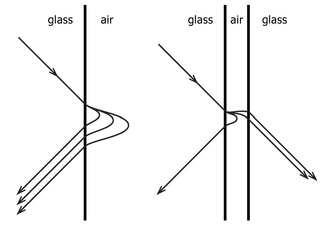
Figure 18:
Cartoon sketch illustrating a light wave, which is normally reflected at a glass/air interface and may have a small amplitude leaking into the air. If another piece of glass is placed near the first (the separation should be no more than a few wavelengths of the light), then the wave may be able to propagate into the second material. A similar phenomenon occurs with matter waves during quantum mechanical tunneling.
Cartoon sketch illustrating a light wave, which is normally reflected at a glass/air interface and may have a small amplitude leaking into the air. If another piece of glass is placed near the first (the separation should be no more than a few wavelengths of the light), then the wave may be able to propagate into the second material. A similar phenomenon occurs with matter waves during quantum mechanical tunneling.
One of the most fantastic aspects of quantum mechanics, and one that provides dramatic confirmation that there is a wavelike aspect to the motion of matter, is that this “leakage effect” is observed for electrons, protons, and neutrons. Here, instead of light and a sheet of glass, consider an electron in a metal or semiconductor. Instead of a glass-air interface, there might be a barrier at the surface of the conductor, either the vacuum of empty space or some other electrical insulator. The electron would normally not have enough energy to leave the conducting material and would be reflected at this surface. If another conductor is placed on the other side of the barrier, and if this barrier is not too thick compared to the electron’s de Broglie wavelength, then there is a probability that the matter-wave can extend through the gap. Even though the electron does not have sufficient energy to jump or spark across the gap, as its quantum mechanical wave function leaks through the forbidden barrier into the second region, it can thus be found in the second conductor.
Other books
One Rough Night (BWWM Motorcycle Erotic Romance) by Monroe, Tasha
Circle of Stones by Suzanne Alyssa Andrew
Completely Smitten by Kristine Grayson
The Secret Ways of Perfume by Cristina Caboni
In the Heart of Forever by Jo-Anna Walker
Suzie and the Monsters by Francis Franklin
Going Rogue by Jessica Jefferson
Branded by Ana J. Phoenix
Ain't No Wifey 2 by Jahquel J.
El sueño de los justos by Francisco Pérez de Antón