The Amazing Story of Quantum Mechanics (28 page)
Read The Amazing Story of Quantum Mechanics Online
Authors: James Kakalios
A patent for a laser, capable of projecting a high-intensity beam of visible light, designed by Charles H. Townes and Arthur L. Schawlow at Bell Labs, was filed in 1958, and in 1960 Theodore H. Maiman at Hughes Research Laboratory in California successfully constructed the first working device. At his press conference in 1960, Maiman was peppered with journalists’ questions about whether he had in fact invented a death ray. When speaking to the public, scientists from Bell Labs were instructed by management to deflect any questions concerning using the laser as a lethal weapon and took pains to avoid saying anything that might be misconstrued or misquoted. Yeah, good luck with that. In 1961, the report in the
Detroit News
of a lecture by a Bell Labs scientist involved in their laser program prominently featured “Death Ray” as the invention’s first potential application. Four years after Maiman’s announcement, in 1964’s MGM film
Goldfinger
James Bond is threatened with a slow, painful death while strapped to a table. The circular buzz saw of the 1959 novel was replaced in the movie with a high-power industrial laser, its beam slowly moving along the length of the table on a trajectory intended to bisect Agent 007.
Detroit News
of a lecture by a Bell Labs scientist involved in their laser program prominently featured “Death Ray” as the invention’s first potential application. Four years after Maiman’s announcement, in 1964’s MGM film
Goldfinger
James Bond is threatened with a slow, painful death while strapped to a table. The circular buzz saw of the 1959 novel was replaced in the movie with a high-power industrial laser, its beam slowly moving along the length of the table on a trajectory intended to bisect Agent 007.
The physics of the laser is essentially that of a glow-in-the-dark solid. Depending on their chemical composition and material properties, lasers can emit not just green light, but red, green, blue, ultraviolet, or infrared photons. The two big differences between lasers and glow-in-the-dark solids is that in lasers, the mezzanine levels are nearly completely occupied with electrons, and, more important, when the electrons in the mezzanine level drop down to the ground state, they all do so at the same time.
How can one ensure that all the electrons residing in the laser levels will choose to drop down to the ground state, emitting photons, simultaneously? Consider the auditorium analogy for a solid, shown in Figure 35.
60
I use essentially the same argument as for the glow-in-the-dark situation from the last chapter. Electrons from the filled orchestra level are promoted up to the balcony by, for example, the absorption of light, or an electrical current. The electrons excited up into the balcony leave behind empty seats in the orchestra. The transition rate is high for electrons to go from the orchestra to the balcony, and it is similarly easy for these electrons to drop back down into the orchestra, emitting light as they do so. Occasionally, an electron will not fall from the balcony to the orchestra, but into a mezzanine seat instead. The transition rate into or out of these mezzanine levels is very low, so once the electron is in one of these quantum states it will stay there for quite some time. If electrons can be excited up to the balcony, and from there to the mezzanine, faster than they spontaneously drop down from the mezzanine level back to the orchestra, then we can obtain a situation where we have nearly as many electrons in the mezzanine level as in the orchestra.
60
I use essentially the same argument as for the glow-in-the-dark situation from the last chapter. Electrons from the filled orchestra level are promoted up to the balcony by, for example, the absorption of light, or an electrical current. The electrons excited up into the balcony leave behind empty seats in the orchestra. The transition rate is high for electrons to go from the orchestra to the balcony, and it is similarly easy for these electrons to drop back down into the orchestra, emitting light as they do so. Occasionally, an electron will not fall from the balcony to the orchestra, but into a mezzanine seat instead. The transition rate into or out of these mezzanine levels is very low, so once the electron is in one of these quantum states it will stay there for quite some time. If electrons can be excited up to the balcony, and from there to the mezzanine, faster than they spontaneously drop down from the mezzanine level back to the orchestra, then we can obtain a situation where we have nearly as many electrons in the mezzanine level as in the orchestra.
We are now ready for some laser action, as shown in Figure 36. There are two ways that an electron in the mezzanine band can return to an empty seat in the orchestra—it can fall or it can be pushed. The transition rate for an electron to spontaneously fall from the mezzanine to the orchestra can be, for some materials, up to a hundred million times slower than for the electron to move from the balcony to the orchestra. This was why we needed to go through the balcony levels in order to populate this intermediate energy band. What could push an electron down to the orchestra? Light.
During the transition from the mezzanine to the orchestra, the electron’s wave function can be expressed as the overlap of the orchestra and mezzanine quantum states. During this process the electron’s average location may be considered to oscillate between its value for each state. An oscillating electric charge emits electromagnetic waves at the frequency of vibration. A formal quantum mechanical analysis of this process finds that the energy emitted is in a discrete packet of energy (that is, a photon) whose energy corresponds to the energy difference between the mezzanine and orchestra levels.
61
61
Once a photon is emitted, this quantum of the electromagnetic wave can induce oscillations in another electron up in the mezzanine level, making it easier for this second electron to jump down into the orchestra, emitting its own light quantum in the process. This second photon can stimulate another electron to make the transition, generating yet another photon with an energy given by the separation of the mezzanine and orchestra bands. In this way a cascade of falling electrons, each induced (pushed) by the oscillating electric field of a light quantum, results. One photon in therefore leads to potentially trillions of photons out, all with exactly the same energy, emitted all at the same time. As the photons are fast, as in speed-of-light fast, there is no noticeable time lag between the first electron falling from the mezzanine and the trillions of electrons stimulated by other photons. The device produces
l
ight
a
mplification by
s
timulated
e
mission of
r
adiation and is called a “laser” for short.
l
ight
a
mplification by
s
timulated
e
mission of
r
adiation and is called a “laser” for short.
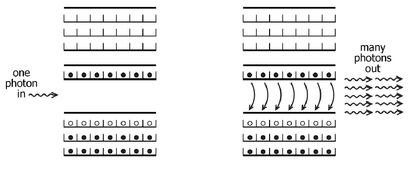
Figure 36:
The auditorium model from the last chapter, only now the occupation of the mezzanine level is quite high. A single photon can stimulate an electron in the mezzanine to drop down to an empty seat in the orchestra, emitting a photon in the process. This photon can in turn induce another electron to make this transition, with the net effect that a very large number of electrons may be stimulated into dropping down to the lower energy band, all emitting identical energy photons. This procedure is the basic physical mechanism underlying the laser.
The auditorium model from the last chapter, only now the occupation of the mezzanine level is quite high. A single photon can stimulate an electron in the mezzanine to drop down to an empty seat in the orchestra, emitting a photon in the process. This photon can in turn induce another electron to make this transition, with the net effect that a very large number of electrons may be stimulated into dropping down to the lower energy band, all emitting identical energy photons. This procedure is the basic physical mechanism underlying the laser.
Of course, if I want this stimulated emission of light to occur more than once, I have to continue to excite electrons up to the balcony level, so that I can maintain the population inversion of electrons in the mezzanine. Thus, it will take a great deal of energy to run the laser. The more photons that I want to be emitted per second, the more energy I have to expend maintaining the occupancy of the mezzanine level. A laser pointer used in a lecture presentation is relatively low intensity and can be run from two AA or AAA batteries, while the high-power versions used in industrial-laser cutting procedures require a thousand Watts of power, enough energy to run a standard household.
Lasers make use of the fact that the emitted light is coherent (that is, all the light waves are in phase with one another, as in the constructive interference example from Chapter 2, Figure 4). The material that is being stimulated to emit photons is typically housed in a long cylinder, both ends of which are mirrored, with one end having a small hole for light to escape. Consequently all the walls of the auditorium reflect photons, and only those light quanta moving in exactly the right direction toward the single exit will depart the hall.
62
Those photons that do not leave the chamber will bounce back and forth, inducing more transitions from the mezzanine to the lower level. The laser light thus forms a tightly focused beam, and as the photons are in phase, they will exhibit minimal spreading upon leaving the laser cavity. Laser light is therefore invisible unless you look directly at the aperture of the laser cylinder, unlike incandescent lightbulbs, from which the illumination spreads out uniformly in all directions. We can see light from an incandescent bulb regardless of where we are looking, but in a sense these photons’ energies are wasted, as light is hitting objects I don’t care about seeing. The laser beam can be seen only if it reflects off a surface. If there is no dust or particulates in the air to scatter the laser beam, the only way to see it is when it gets to where it is going. A tight, narrow laser beam, sent out from a lab on Earth, was measured to have broadened out to a width of only about two miles after traveling 240,000 miles to the moon.
62
Those photons that do not leave the chamber will bounce back and forth, inducing more transitions from the mezzanine to the lower level. The laser light thus forms a tightly focused beam, and as the photons are in phase, they will exhibit minimal spreading upon leaving the laser cavity. Laser light is therefore invisible unless you look directly at the aperture of the laser cylinder, unlike incandescent lightbulbs, from which the illumination spreads out uniformly in all directions. We can see light from an incandescent bulb regardless of where we are looking, but in a sense these photons’ energies are wasted, as light is hitting objects I don’t care about seeing. The laser beam can be seen only if it reflects off a surface. If there is no dust or particulates in the air to scatter the laser beam, the only way to see it is when it gets to where it is going. A tight, narrow laser beam, sent out from a lab on Earth, was measured to have broadened out to a width of only about two miles after traveling 240,000 miles to the moon.
Thanks to the quantization of energy levels, when the electrons drop from the mezzanine to the lower-energy orchestra in response to the photon stimulation, they will all emit light of exactly the same energy. The light from a laser will thus be of a single frequency, that is, one color, with remarkably small variations. An efficient mechanism to generate red laser light is to use a mixture of two gases, helium and neon. Both of these elements have completely filled outer quantum levels (as shown in Figure 31b) and are thus chemically inert—they do not lower their energy by forming any type of chemical bond. When an electron beam is passed through this gas mixture, the kinetic energy of the electron current can be transferred when it collides with a helium atom. An electron in the helium atom is excited from the ground state to an “excited state”—which we have been terming the balcony level. The spacing of their quantum levels is such that when the helium atom with its electron in the higher-energy state collides with a neon atom, it promotes an electron into a very long-lived excited state in the neon atom that acts as the mezzanine level. When light of the necessary frequency stimulates the neon atoms, they drop back to their ground state, emitting red photons.
By using electrically charged (that is, ionized) argon gas instead of a helium-neon mixture, green light can be produced. Using semiconducting diodes (much more on this in the next chapter), one can dispense with the gases and construct a completely solid-state laser, capable of producing red, green, or even blue light. Red light has a lower energy, of 1.9 electron Volts, and longer wavelength (about 650 nanometers) compared to blue light’s photon energy of 2.6 electron Volts and a wavelength of 475 nanometers. The difference in wavelength may not seem like much, but it makes a big difference in your DVD player.
Anyone who has closely examined an old-style newspaper photograph, composed of a series of black and white dots, understands that the information contained in an image may be relayed via a series of pixels. Digital versatile discs (DVDs) and compact discs (CDs) encode images and sound or just sound, respectively, through a set of instructions for either a video display or audio system. Pixels are binary, in that they have just two states: on or off, bright or dark. All digital data representation basically involves strings of “ons” and “offs,” often referred to as “ones” or “zeros.”
The development of inexpensive, compact solid-state lasers enables one to “read” the storage of these ones and zeros on a disc. A laser is bounced off the shiny side of the disc, and the reflected light is detected by an optical sensor. If the surface of the disc is smooth, then the laser light, which travels in a straight line, will be reflected directly onto the optical detector, and that location on the disc will be recorded as being a bright spot. If the laser light falls on a region of the disc that is distorted (for example, at the edge of a little pit gouged into the disc or a bump protruding from the surface), then the light will scatter in some random direction and not be reflected onto the optical detector. The detector will thus indicate a dark spot at this location of the disc. Calling the bright spot a “zero” and the dark spot a “one,” we can store and transmit digital information.
Moving the laser along the disc, one can record the sequence of smooth and rough regions and translate that into ones and zeros, which in turn can be decoded to make beautiful music. Actually, it’s easier to keep the laser fixed and move the disc underneath it (rotating the disc at high speed—typically at several hundred revolutions per minute) as the laser spot is moved from the center of the disc to its outer edge. The higher the density of ones and zeros (that is, the more bits of information in a given length), the higher the resolution of the video or audio signal. Here is where innovations in laser technology, thanks to quantum mechanics, have had a real impact on consumer entertainment technology.
If you wish to paint a two-inch-high statuette of an Orc (to take a random geeky example), you do not use the same large brush you would use for painting your house (assuming you are interested in doing more than just glopping a single color of paint on the figure). In order to apply different colors over the small details on the tiny character, you will need a very fine brush that would make house painting tedious but is well suited for the detailed work on the statuette. When light is used as a probe, the wavelength plays the same role as the fineness of the brush’s bristles. One cannot use a wave to detect features smaller than the spacing between the peaks or troughs of the wave.
This is why optical microscopes, using visible light whose wavelengths are on the order of several hundred nanometers, are not able to let us see viruses or other nanometer-scale objects, regardless of the focusing. To “see” such small-scale structures, either you need light with a wavelength on the order of nanometers or smaller (such as high-energy X-rays, which lead to the necessity to develop X-ray lenses and focusing procedures) or you can employ electrons. The de Broglie wavelength of electrons can be adjusted by varying the momentum, which is easy to control by changing the magnitude of the accelerating voltage acting on the electron beam, and a series of charged plates can focus the electron beam. Detection of the current either reflected from a surface or transmitted through a thin sample can thereby provide “images” with atomic-scale resolution, and these electron microscopes are another example of quantum mechanics in action.
Other books
The Train Was On Time by Heinrich Boll
Stories from Islamic History by Nayab Naseer
The Seraphim Sequence: The Fifth Column 2 by Farrugia, Nathan M
Singapore Fling by Rhian Cahill
Heaven Scent by SpursFanatic
Rogue Alpha: Wolf Shifter Romance (Wild Lake Wolves Book 1) by White, Kimber
Isvik by Innes, Hammond;
Curtis's Dads 23 by Lynn Hagen
Amelia by Marie, Bernadette
Foxglove Summer by Ben Aaronovitch