The Amazing Story of Quantum Mechanics (23 page)
Read The Amazing Story of Quantum Mechanics Online
Authors: James Kakalios
Right away, from the fact that electrons have an intrinsic angular momentum of
ħ
/2, we can understand the structure of the periodic table of the elements. In Chapter 6 we discussed the solutions to Schrödinger’s equation when the potential V is that of the electrical attraction between the negatively charged electrons and the positively charged nucleus. Schrödinger found that there were a series of possible solutions corresponding to different energy states that we argued were not unlike a series of rows of seats in a classroom, sketched in Figure 15. Some seats are close to the front of the classroom, while there are other rows farther from the front of the room. The configuration of the rows of seats depends only on the attractive force between the positive nucleus and the negative electron. We now understand why all the electrons in an atom don’t just pile up in the chair in the front row, which is the lowest-energy quantum state available. For if they were to do that, then all of the electrons would be in the same location in the same quantum state, and as we have just shown, the probability of that happening is zero.
ħ
/2, we can understand the structure of the periodic table of the elements. In Chapter 6 we discussed the solutions to Schrödinger’s equation when the potential V is that of the electrical attraction between the negatively charged electrons and the positively charged nucleus. Schrödinger found that there were a series of possible solutions corresponding to different energy states that we argued were not unlike a series of rows of seats in a classroom, sketched in Figure 15. Some seats are close to the front of the classroom, while there are other rows farther from the front of the room. The configuration of the rows of seats depends only on the attractive force between the positive nucleus and the negative electron. We now understand why all the electrons in an atom don’t just pile up in the chair in the front row, which is the lowest-energy quantum state available. For if they were to do that, then all of the electrons would be in the same location in the same quantum state, and as we have just shown, the probability of that happening is zero.
There’s a fancy term used to describe the fact that no two electrons can ever be in the same position in the same quantum state—the Pauli exclusion principle. Wolfgang Pauli, one of the founding fathers of quantum mechanics, postulated this principle in 1925 in order to account for the configuration of electrons in elements. Hydrogen with one electron has the lowest energy state occupied, shown in Figure 31a. As there is only one electron in this element, it is exempt from the exclusion principle. The next element in the periodic table is helium, with two electrons. We now extend this physical analogy and propose that each “seat” in the auditorium is actually a “love seat” that can accommodate two electrons, provided that they face away from each other (that is, as long as one is spin “up” and the other is spin “down.”
49
As in Figure 31b, both of these electrons can reside in the lowest energy state, as long as one has a spin value of +
ħ
/2 and the other has a spin of -
ħ
/2, since each spin state counts as a different quantum state. As there are no other possible spin values, a third electron in lithium (the next element up the table, shown in Figure 31c) will have to reside in the next higher energy state. If all three electrons were to reside in the lowest energy state in lithium, then there would be at least two electrons both with spin = +
ħ
/2 or spin = -
ħ
/2, and the probability of this occurring is Ψ
2
= 0. Carbon, shown in Figure 31d, has six electrons—two sit in the ground state, and the remaining four sit in the next highest “row of seats”—and is able to form chemical bonds in a wide variety of ways. By forming these bonds, the carbon atom and the other atoms it chemically interacts with lower their energies, compared to their unbonded states. If all of carbon’s six electrons could drop down into the lowest energy state, there would be no energetic advantage to forming chemical bonds with other atoms. Consequently, there would be no methane, no diamond, no DNA, without the Pauli exclusion principle.
49
As in Figure 31b, both of these electrons can reside in the lowest energy state, as long as one has a spin value of +
ħ
/2 and the other has a spin of -
ħ
/2, since each spin state counts as a different quantum state. As there are no other possible spin values, a third electron in lithium (the next element up the table, shown in Figure 31c) will have to reside in the next higher energy state. If all three electrons were to reside in the lowest energy state in lithium, then there would be at least two electrons both with spin = +
ħ
/2 or spin = -
ħ
/2, and the probability of this occurring is Ψ
2
= 0. Carbon, shown in Figure 31d, has six electrons—two sit in the ground state, and the remaining four sit in the next highest “row of seats”—and is able to form chemical bonds in a wide variety of ways. By forming these bonds, the carbon atom and the other atoms it chemically interacts with lower their energies, compared to their unbonded states. If all of carbon’s six electrons could drop down into the lowest energy state, there would be no energetic advantage to forming chemical bonds with other atoms. Consequently, there would be no methane, no diamond, no DNA, without the Pauli exclusion principle.
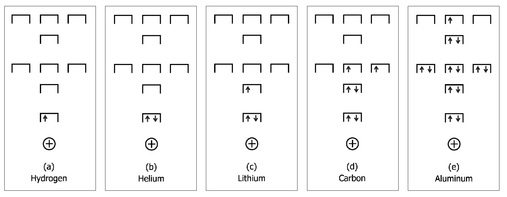
Figure 31:
Representation of the allowed quantum state solutions to the Schröedinger equation for an electron in an atom as a set of seats in a classroom. The Pauli principle indicates that each seat can accommodate two electrons provided they have opposite spins. Shown from left to right are the occupied quantum states for atoms containing one, two, three, six, and thirteen electrons, corresponding to hydrogen, helium, lithium, carbon, and aluminum, respectively.
Representation of the allowed quantum state solutions to the Schröedinger equation for an electron in an atom as a set of seats in a classroom. The Pauli principle indicates that each seat can accommodate two electrons provided they have opposite spins. Shown from left to right are the occupied quantum states for atoms containing one, two, three, six, and thirteen electrons, corresponding to hydrogen, helium, lithium, carbon, and aluminum, respectively.
Consider an atom such as aluminum, with thirteen electrons, shown in Figure 31e. All but one of these electrons are arranged in +
ħ
/2 and -
ħ
/2 pairs, and thus only this last electron can participate in chemical bonds. The other twelve electrons are chemically inert and form the inner core of the aluminum atoms. Not that we can’t make use of these inner electrons. The Pauli principle forces the electrons to reside in higher and higher energy states, equivalent to having some students sit in rows far from the front of the classroom, even when the atom is in its lowest energy configuration. If we could knock one of the electrons out of the ground state (a row close to the front of the lecture hall), then an empty position suddenly would open up, as if we had ejected a student sitting in a front-row seat. A student sitting in one of the upper rows could then jump down into the newly vacant seat. Just such a situation can arise when a high-energy beam of electrons strikes an atom. In that case, when one of the outer electrons falls down to occupy the lower energy state, it can emit an X-ray photon during the transition. This is in fact a very efficient way to generate X-rays, and most dental X-ray machines employ electron currents striking a copper target to create the penetrating radiation.
ħ
/2 and -
ħ
/2 pairs, and thus only this last electron can participate in chemical bonds. The other twelve electrons are chemically inert and form the inner core of the aluminum atoms. Not that we can’t make use of these inner electrons. The Pauli principle forces the electrons to reside in higher and higher energy states, equivalent to having some students sit in rows far from the front of the classroom, even when the atom is in its lowest energy configuration. If we could knock one of the electrons out of the ground state (a row close to the front of the lecture hall), then an empty position suddenly would open up, as if we had ejected a student sitting in a front-row seat. A student sitting in one of the upper rows could then jump down into the newly vacant seat. Just such a situation can arise when a high-energy beam of electrons strikes an atom. In that case, when one of the outer electrons falls down to occupy the lower energy state, it can emit an X-ray photon during the transition. This is in fact a very efficient way to generate X-rays, and most dental X-ray machines employ electron currents striking a copper target to create the penetrating radiation.
How do the last few electrons that are not residing in paired quantum states, and are thus available to participate in chemical bonds, combine with those from neighboring aluminum atoms to hold all trillion trillion atoms together in a solid piece of aluminum? How do the last unpaired electrons between carbon atoms in diamond combine to bind this rigid insulator? In both cases, the electrons arrange themselves to satisfy the Pauli exclusion principle, though the resulting material properties in aluminum and diamond could not be more different.
One easy way to satisfy the Pauli principle is to never let the electrons be at the same place at the same time. If I have a line of atoms, and next to each atom is a barrier, then I can place an electron inside each theoretical box (we’ll see soon what this “box” really is), and all these negative charges can be in the same quantum state. This does not cause any problem, for by creating a series of containers for each electron, I have in principle made them distinguishable. I can tell which electron is in the box on the right and which on the left, just as I could tell apart the two stones that I tossed into the pond. The walls of the boxes prevent the de Broglie waves of each electron from overlapping with those of its neighbors, so the trillion trillion electrons can all be in the same quantum state, as the total wave function is just the one electron function repeated a trillion trillion times. Each electron is described by its own ribbon, as shown in Figure 30, and no ribbon is used for more than one electron. When I calculate the average energy of each electron in a box, assuming the width of the box is the spacing between atoms in my solid, I arrive at a number of about three electron Volts (the exact value obviously depends on all sorts of details of how the atoms in the solid are arranged—termed the crystalline configuration). This is the energy I would have to give to an electron to remove it from the box. Of course, as each electron has two possible values of spin, I can actually put two electrons in each box (each box contains a love seat), as long as they have intrinsic angular momentum +
ħ
/2 and -
ħ
/2.
ħ
/2 and -
ħ
/2.
Consider carbon, shown in Figure 31d. Carbon can easily “rearrange the seats in the rows” of the four upper electrons, mixing the quantum mechanical wave functions to form differing configurations of quantum states that allow for a variety of chemical interactions. Carbon can form strong bonds in a straight line, in proteins and DNA; it can form graphite, with three strong bonds in a plane and one weak bond above or below the plane, which is why graphite can be easily peeled apart when used in a pencil, for example; and when the “seats” are configured to form four equally strong bonds, we call this form of carbon “diamond.” In each case, the carbon atom has four electrons that are capable of participating in chemical bonds, represented by four boxes, each of which holds one electron. The Pauli principle tells us that each box can hold a second electron, provided it has an opposite spin from the first. When two carbon atoms come close enough to each other that the quantum states containing these unpaired electrons overlap, the two electrons can be represented by a two-electron wave function. It turns out that each of the unpaired electrons can lower its energy if the electrons fill up the love seats in each box (Figure 32a). That is, I must add energy to the atoms to remove the electrons from these boxes, and restore each one to its unpaired state. The overlapping electron wave functions form a chemical bond between the atoms, holding them together in the crystalline solid. The Pauli principle is satisfied by the localization of the electrons in space. In a diamond crystal, each carbon is surrounded by four other carbon atoms in a tetrahedral arrangement, and their unpaired electrons can occupy the second seat in the first atom’s boxes (Figure 32b).
But there is another way to satisfy the Pauli exclusion principle. Let’s say that there are no boxes, and I let the electrons wander over the entire solid. In this case two electrons can be at the same place at the same time, so I have to ensure that they are each in different quantum states. How many different lowest-energy quantum levels are available for the last unpaired electron, such as the thirteenth electron for aluminum, shown in Figure 31e? As many as there are atoms in the solid. Since I have given up having any knowledge of where the electrons may be, I can compensate by having the electrons reside in states that have a well-defined momentum. I can have a matter wave with a very large wavelength, equal to the entire length of the solid. Since (momentum) × (wavelength) = Planck’s constant, this large wavelength corresponds to a very small momentum, and hence energy. At the other extreme, the smallest wavelength that can be constructed corresponds to the distance between atoms in the solid. This is very short, so the momentum of this matter-wave is high. The highest energy of this shortest wavelength is
also
about three electron Volts, again, depending on the details of the atomic configurations in the solid.
also
about three electron Volts, again, depending on the details of the atomic configurations in the solid.
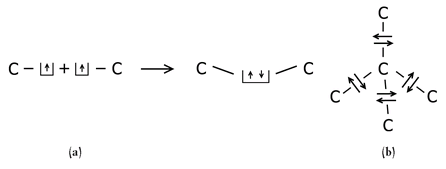
Figure 32:
Sketch of the lowering in energy when two unpaired electrons from adjacent carbon atoms overlap and form a carbon-carbon bond (a). Also shown is a sketch of the configuration of carbon when in the diamond configuration, allowing four chemical binds with its neighbors, in a tetrahedral orientation (b).
Sketch of the lowering in energy when two unpaired electrons from adjacent carbon atoms overlap and form a carbon-carbon bond (a). Also shown is a sketch of the configuration of carbon when in the diamond configuration, allowing four chemical binds with its neighbors, in a tetrahedral orientation (b).
So, whether the electrons are put inside boxes in each atom, or allowed to roam over the solid, we still wind up with an energy of about three electron Volts. However, in the second situation, where the electrons can move around the solid in discrete momentum states, three electron Volts is approximately the energy of the
most
energetic electron, while when the electrons are placed in boxes, three electron Volts is roughly the energy of
each
electron. The average energy of an electron in the free-to-roam case is less than three electron Volts, and in fact will be closer to 1.5 electron Volts (recall the class from our discussion of the Heisenberg uncertainty principle, where every student had a different exam score, from 0 to 100. In this case the average grade was 50 percent). For the electrons-in-a-box situation, every electron has the same energy, so the average energy is also three electron Volts (if every student scores a perfect 100 percent, then the class average is also 100 percent). Consequently, depending on its chemical composition, the solid as a whole can lower its energy by letting the electrons wander around the crystal. This won’t be true for all solids. Some materials will be able to lower their total energy by keeping every electron localized in boxes around each atom. We call the free-to-roam cases “metals,” and the electrons-in-a-box materials “insulators.”
most
energetic electron, while when the electrons are placed in boxes, three electron Volts is roughly the energy of
each
electron. The average energy of an electron in the free-to-roam case is less than three electron Volts, and in fact will be closer to 1.5 electron Volts (recall the class from our discussion of the Heisenberg uncertainty principle, where every student had a different exam score, from 0 to 100. In this case the average grade was 50 percent). For the electrons-in-a-box situation, every electron has the same energy, so the average energy is also three electron Volts (if every student scores a perfect 100 percent, then the class average is also 100 percent). Consequently, depending on its chemical composition, the solid as a whole can lower its energy by letting the electrons wander around the crystal. This won’t be true for all solids. Some materials will be able to lower their total energy by keeping every electron localized in boxes around each atom. We call the free-to-roam cases “metals,” and the electrons-in-a-box materials “insulators.”
And that’s how quantum mechanics explains solid-state physics. At very low temperatures, all solids either conduct electricity or they don’t. We call the first case metals, and the second are insulators (the distinction between insulators and semiconductors is most relevant around room temperature, and I defer for now a discussion of the differences between the two).
Metals such as aluminum are good conductors of electricity because the outermost electrons satisfy the Pauli principle by residing in momentum states and are free to move around the entire solid, while insulators keep theirs in boxes (bonds) around each atom. To remove a metal atom from the solid, I must first grab one of the free-range electrons and localize it on a positively charged atom—in essence, put it in a box so that I can pull the neutral atom out of the solid. But this costs me a few electron Volts of energy, and this can be considered the binding energy holding the atoms together in the metal. There are no directional bonds between atoms, so it is easy to move atoms past each other, which is why metals are easy to pull into wires or pound into thin sheets, without losing their structural coherence. If light is absorbed by the solid, there is always a free electron that can absorb its energy and reemit it back again, which is why metals are reflective and shiny. The sea of free electrons makes metals good conductors of both electrical current and heat.
Other books
Marius' Mules VI: Caesar's Vow by S.J.A. Turney
Mostly Harmless by Douglas Adams
Salvage by Jason Nahrung
Little Birds by Anais Nin
A Deadly Shaker Spring by Deborah Woodworth
Healed by Hope by Jim Melvin
Secrets [5] Echoes: Part One by A.M. Hudson
Five Minute Man: A Contemporary Love Story by Zanders, Abbie
A Slice of Honeybear Pie (BWWM Paranormal BBW Bear Shifter Romance) (Bearfield Book 1) by Jacqueline Sweet, Eva Wilder
Saving Scarlett by R. E. Butler