The Code Book (14 page)
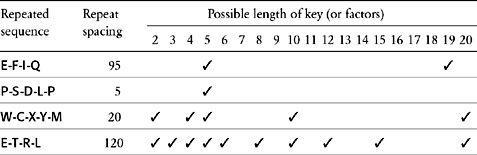
The first stage in Babbage’s cryptanalysis is to look for sequences of letters that appear more than once in the ciphertext. There are two ways that such repetitions could arise. The most likely is that the same sequence of letters in the plaintext has been enciphered using the same part of the key. Alternatively, there is a slight possibility that two different sequences of letters in the plaintext have been enciphered using different parts of the key, coincidentally leading to the identical sequence in the ciphertext. If we restrict ourselves to long sequences, then we largely discount the second possibility, and, in this case, we shall consider repeated sequences only if they are of four letters or more.
Table 8
is a log of such repetitions, along with the spacing between the repetition. For example, the sequence E-F-I-Q appears in the first line of the ciphertext and then in the fifth line, shifted forward by 95 letters.
As well as being used to encipher the plaintext into ciphertext, the keyword is also used by the receiver to decipher the ciphertext back into plaintext. Hence, if we could identify the keyword, deciphering the text would be easy. At this stage we do not have enough information to work out the keyword, but
Table 8
does provide some very good clues as to its length. Having listed which sequences repeat themselves and the spacing between these repetitions, the rest of the table is given over to identifying the
factors
of the spacing—the numbers that will divide into the spacing.

Figure 13
The ciphertext, enciphered using the Vigenère cipher.
For example, the sequence W-C-X-Y-M repeats itself after 20 letters, and the numbers 1, 2, 4, 5, 10 and 20 are factors, because they divide perfectly into 20 without leaving a remainder. These factors suggest six possibilities:
(1) The key is 1 letter long and is recycled 20 times between encryptions.
(2) The key is 2 letters long and is recycled 10 times between encryptions.
(3) The key is 4 letters long and is recycled 5 times between encryptions.
(4) The key is 5 letters long and is recycled 4 times between encryptions.
(5) The key is 10 letters long and is recycled 2 times between encryptions.
(6) The key is 20 letters long and is recycled 1 time between encryptions.
The first possibility can be excluded, because a key that is only 1 letter long gives rise to a monoalphabetic cipher—only one row of the Vigenère square would be used for the entire encryption, and the cipher alphabet would remain unchanged; it is unlikely that a cryptographer would do this. To indicate each of the other possibilities, a ✓ is placed in the appropriate column of
Table 8
. Each ✓ indicates a potential key length.
To identify whether the key is 2, 4, 5, 10 or 20 letters long, we need to look at the factors of all the other spacings. Because the keyword seems to be 20 letters or smaller,
Table 8
lists those factors that are 20 or smaller for each of the other spacings. There is a clear propensity for a spacing divisible by 5. In fact, every spacing is divisible by 5. The first repeated sequence, E-F-I-Q, can be explained by a keyword of length 5 recycled nineteen times between the first and second encryptions. The second repeated sequence, P-S-D-L-P, can be explained by a keyword of length 5 recycled just once between the first and second encryptions. The third repeated sequence, W-C-X-Y-M, can be explained by a keyword of length 5 recycled four times between the first and second encryptions. The fourth repeated sequence, E-T-R-L, can be explained by a keyword of length 5 recycled twenty-four times between the first and second encryptions. In short, everything is consistent with a five-letter keyword.
Table 8
Repetitions and spacings in the ciphertext.
Assuming that the keyword is indeed 5 letters long, the next step is to work out the actual letters of the keyword. For the time being, let us call the keyword L
1
-L
2
-L
3
-L
4
-L
5
, such that L
1
represents the first letter of the keyword, and so on. The process of encipherment would have begun with enciphering the first letter of the plaintext according to the first letter of the keyword, L
1
. The letter L
1
defines one row of the Vigenère square, and effectively provides a monoalphabetic substitution cipher alphabet for the first letter of the plaintext. However, when it comes to encrypting the second letter of the plaintext, the cryptographer would have used L
2
to define a different row of the Vigenère square, effectively providing a different monoalphabetic substitution cipher alphabet. The third letter of plaintext would be encrypted according to L
3
, the fourth according to L
4
, and the fifth according to L
5
. Each letter of the keyword is providing a different cipher alphabet for encryption. However, the sixth letter of the plaintext would once again be encrypted according to L
1
, the seventh letter of the plaintext would once again be encrypted according to L
2
, and the cycle repeats itself thereafter. In other words, the polyalphabetic cipher consists of five monoalphabetic ciphers, each monoalphabetic cipher is responsible for encrypting one-fifth of the entire message, and, most importantly, we already know how to cryptanalyze monoalphabetic ciphers.
We proceed as follows. We know that one of the rows of the Vigenère square, defined by L
1
, provided the cipher alphabet to encrypt the 1st, 6th, 11th, 16th, … letters of the message. Hence, if we look at the 1st, 6th, 11th, 16th, … letters of the ciphertext, we should be able to use old-fashioned frequency analysis to work out the cipher alphabet in question.
Figure 14
shows the frequency distribution of the letters that appear in the 1st, 6th, 11th, 16th, … positions of the ciphertext, which are W, I, R, E,.… At this point, remember that each cipher alphabet in the Vigenère square is simply a standard alphabet shifted by a value between 1 and 26. Hence, the frequency distribution in
Figure 14
should have similar features to the frequency distribution of a standard alphabet, except that it will have been shifted by some distance. By comparing the L
1
distribution with the standard distribution, it should be possible to work out the shift.
Figure 15
shows the standard frequency distribution for a piece of English plaintext.
The standard distribution has peaks, plateaus and valleys, and to match it with the L
1
cipher distribution we look for the most outstanding combination of features. For example, the three spikes at R-S-T in the standard distribution (
Figure 15
) and the long depression to its right that stretches across six letters from U to Z together form a very distinctive pair of features. The only similar features in the L
1
distribution (
Figure 14
) are the three spikes at V-W-X, followed by the depression stretching six letters from Y to D. This would suggest that all the letters encrypted according to L
1
have been shifted four places, or that L
1
defines a cipher alphabet which begins E, F, G, H,.… In turn, this means that the first letter of the keyword, L
1
, is probably E. This hypothesis can be tested by shifting the L
1
distribution back four letters and comparing it with the standard distribution.
Figure 16
shows both distributions for comparison. The match between the major peaks is very strong, implying that it is safe to assume that the keyword does indeed begin with E.

Figure 14
Frequency distribution for letters in the ciphertext encrypted using the L
1
cipher alphabet (number of occurrences).
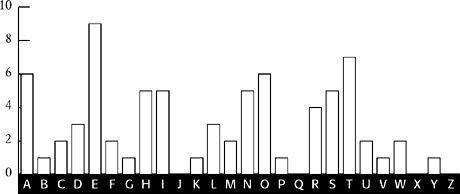
Figure 15
Standard frequency distribution (number of occurrences based on a piece of plaintext containing the same number of letters as in the ciphertext).
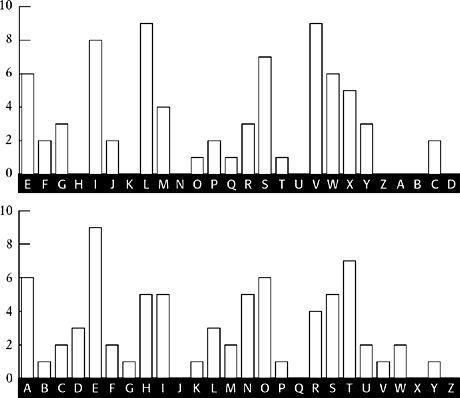
Figure 16
The L
1
distribution shifted back four letters (top), compared with the standard frequency distribution (bottom). All major peaks and troughs match.
To summarize, searching for repetitions in the ciphertext has allowed us to identify the length of the keyword, which turned out to be five letters long. This allowed us to split the ciphertext into five parts, each one enciphered according to a monoalphabetic substitution as defined by one letter of the keyword. By analyzing the fraction of the ciphertext that was enciphered according to the first letter of the keyword, we have been able to show that this letter, L
1
, is probably E. This process is repeated in order to identify the second letter of the keyword. A frequency distribution is established for the 2nd, 7th, 12th, 17th,… letters in the ciphertext. Again, the resulting distribution, shown in
Figure 17
, is compared with the standard distribution in order to deduce the shift.