The Code Book (42 page)
First, imagine that we wish to encrypt the message HELLO, employing a simple computer version of a transposition cipher. Before encryption can begin, we must translate the message into ASCII according to
Table 24
:
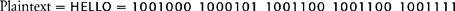
One of the simplest forms of transposition cipher would be to swap the first and second digits, the third and fourth digits, and so on. In this case the final digit would remain unchanged because there are an odd number of digits. In order to see the operation more clearly, I have removed the spaces between the ASCII blocks in the original plaintext to generate a single string, and then lined it up against the resulting ciphertext for comparison:
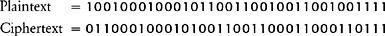
An interesting aspect of transposition at the level of binary digits is that the transposing can happen within the letter. Furthermore, bits of one letter can swap places with bits of the neighboring letter. For example, by swapping the seventh and eighth numbers, the final 0 of H is swapped with the initial 1 of E. The encrypted message is a single string of 35 binary digits, which can be transmitted to the receiver, who then reverses the transposition to re-create the original string of binary digits. Finally, the receiver reinterprets the binary digits via ASCII to regenerate the message HELLO.
Table 24
ASCII binary numbers for the capital letters.

Next, imagine that we wish to encrypt the same message, HELLO, this time employing a simple computer version of a substitution cipher. Once again, we begin by converting the message into ASCII before encryption. As usual, substitution relies on a key that has been agreed between sender and receiver. In this case the key is the word DAVID translated into ASCII, and it is used in the following way. Each element of the plaintext is “added” to the corresponding element of the key. Adding binary digits can be thought of in terms of two simple rules. If the elements in the plaintext and the key are the same, the element in the plaintext is substituted for 0 in the ciphertext. But, if the elements in the message and key are different, the element in the plaintext is substituted for 1 in the ciphertext:

The resulting encrypted message is a single string of 35 binary digits which can be transmitted to the receiver, who uses the same key to reverse the substitution, thus recreating the original string of binary digits. Finally, the receiver reinterprets the binary digits via ASCII to regenerate the message HELLO.
Computer encryption was restricted to those who had computers, which in the early days meant the government and the military. However, a series of scientific, technological and engineering breakthroughs made computers, and computer encryption, far more widely available. In 1947, AT&T Bell Laboratories invented the transistor, a cheap alternative to the electronic valve. Commercial computing became a reality in 1951 when companies such as Ferranti began to make computers to order. In 1953 IBM launched its first computer, and four years later it introduced Fortran, a programming language that allowed “ordinary” people to write computer programs. Then, in 1959, the invention of the integrated circuit heralded a new era of computing.
During the 1960s, computers became more powerful, and at the same time they became cheaper. Businesses were increasingly able to afford computers, and could use them to encrypt important communications such as money transfers or delicate trade negotiations. However, as more and more businesses bought computers, and as encryption between businesses spread, cryptographers were confronted with new problems, difficulties that had not existed when cryptography was the preserve of governments and the military. One of the primary concerns was the issue of standardization. A company might use a particular encryption system to ensure secure internal communication, but it could not send a secret message to an outside organization unless the receiver used the same system of encryption. Eventually, on May 15, 1973, America’s National Bureau of Standards planned to solve the problem, and formally requested proposals for a standard encryption system that would allow business to speak secretly unto business.
One of the more established cipher algorithms, and a candidate for the standard, was an IBM product known as Lucifer. It had been developed by Horst Feistel, a German émigré who had arrived in America in 1934. He was on the verge of becoming a U.S. citizen when America entered the war, which meant that he was placed under house arrest until 1944. For some years after, he suppressed his interest in cryptography to avoid arousing the suspicions of the American authorities. When he did eventually begin research into ciphers, at the Air Force’s Cambridge Research Center, he soon found himself in trouble with the National Security Agency (NSA), the organization with overall responsibility for maintaining the security of military and governmental communications, and which also attempts to intercept and decipher foreign communications. The NSA employs more mathematicians, buys more computer hardware, and intercepts more messages than any other organization in the world. It is the world leader when it comes to snooping.
The NSA did not object to Feistel’s past, they merely wanted to have a monopoly on cryptographic research, and it seems that they arranged for Feistel’s research project to be canceled. In the 1960s Feistel moved to the Mitre Corporation, but the NSA continued to apply pressure and forced him to abandon his work for a second time. Feistel eventually ended up at IBM’s Thomas J. Watson Laboratory near New York, where for several years he was able to conduct his research without being harassed. It was there, during the early 1970s, that he developed the Lucifer system.
Lucifer encrypts messages according to the following scrambling operation. First, the message is translated into a long string of binary digits. Second, the string is split into blocks of 64 digits, and encryption is performed separately on each of the blocks. Third, focusing on just one block, the 64 digits are shuffled, and then split into two half-blocks of 32, labeled Left
0
and Right
0
. The digits in Right
0
are then put through a “mangler function,” which changes the digits according to a complex substitution. The mangled Right
0
is then added to Left
0
to create a new halfblock of 32 digits called Right
1
. The original Right
0
is relabeled Left
1
. This set of operations is called a “round.” The whole process is repeated in a second round, but starting with the new half-blocks, Left
1
and Right
1
, and ending with Left
2
and Right
2
. This process is repeated until there have been 16 rounds in total. The encryption process is a bit like kneading a slab of dough. Imagine a long slab of dough with a message written on it. First, the long slab is divided into blocks that are 64 cm in length. Then, one half of one of the blocks is picked up, mangled, folded over, added to the other half and stretched to make a new block. Then the process is repeated over and over again until the message has been thoroughly mixed up. After 16 rounds of kneading the ciphertext is sent, and is then deciphered at the other end by reversing the process.
The exact details of the mangler function can change, and are determined by a key agreed by sender and receiver. In other words, the same message can be encrypted in a myriad of different ways depending on which key is chosen. The keys used in computer cryptography are simply numbers. Hence, the sender and receiver merely have to agree on a number in order to decide the key. Thereafter, encryption requires the sender to input the key number and the message into Lucifer, which then outputs the ciphertext. Decryption requires the receiver to input the same key number and the ciphertext into Lucifer, which then outputs the original message.
Lucifer was generally held to be one of the strongest commercially available encryption products, and consequently it was used by a variety of organizations. It seemed inevitable that this encryption system would be adopted as the American standard, but once again the NSA interfered with Feistel’s work. Lucifer was so strong that it offered the possibility of an encryption standard that was probably beyond the codebreaking capabilities of the NSA; not surprisingly, the NSA did not want to see an encryption standard that they could not break. Hence, it is rumored that the NSA lobbied to weaken one aspect of Lucifer, the number of possible keys, before allowing it to be adopted as the standard.
The number of possible keys is one of the crucial factors determining the strength of any cipher. A cryptanalyst trying to decipher an encrypted message could attempt to check all possible keys, and the greater the number of possible keys, the longer it will take to find the right one. If there are only 1,000,000 possible keys, a cryptanalyst could use a powerful computer to find the correct one in a matter of minutes, and thereby decipher an intercepted message. However, if the number of possible keys is large enough, finding the correct key becomes impractical. If Lucifer were to become the encryption standard, then the NSA wanted to ensure that it operated with only a restricted number of keys.
The NSA argued in favor of limiting the number of keys to roughly 100,000,000,000,000,000 (technically referred to as 56 bits, because this number consists of 56 digits when written in binary). It seems that the NSA believed that such a key would provide security within the civilian community, because no civilian organization had a computer powerful enough to check every possible key within a reasonable amount of time. However, the NSA itself, with access to the world’s greatest computing resource, would just about be able to break into messages. The 56-bit version of Feistel’s Lucifer cipher was officially adopted on November 23, 1976, and was called the Data Encryption Standard (DES). A quarter of a century later, DES remains America’s official standard for encryption.
The adoption of DES solved the problem of standardization, encouraging businesses to use cryptography for security. Furthermore, DES was strong enough to guarantee security against attacks from commercial rivals. It was effectively impossible for a company with a civilian computer to break into a DES-encrypted message because the number of possible keys was sufficiently large. Unfortunately, despite standardization and despite the strength of DES, businesses still had to deal with one more major issue, a problem known as
key distribution
.