The Information (27 page)
The symbolic version—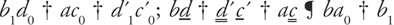 , i.e.
, i.e. —having been suitably drained of meaning, allowed the user to reach the desired conclusion without tripping over awkward intermediate propositions along the lines of “babies are despised.”
—having been suitably drained of meaning, allowed the user to reach the desired conclusion without tripping over awkward intermediate propositions along the lines of “babies are despised.”
As the century turned, Bertrand Russell paid George Boole an extraordinary compliment: “Pure mathematics was discovered by Boole, in a work which he called the
Laws of Thought
.”
♦
It has been quoted often.
What makes the compliment extraordinary is the seldom quoted disparagement that follows on its heels:
He was also mistaken in supposing that he was dealing with the laws of thought: the question how people actually think was quite irrelevant to him, and if his book had really contained the laws of thought, it was curious that no one should ever have thought in such a way before.
One might almost think Russell enjoyed paradoxes.
♦
But Count Miot de Melito claimed in his memoirs that Chappe submitted his idea to the War Office with the name tachygraphe (“swift writer”) and that he, Miot, proposed télégraphe instead—which “has become, so to speak, a household word.”
(No Other Thing Is More Enswathed in the Unknown)
The perfect symmetry of the whole apparatus—the wire in the middle, the two telephones at the ends of the wire, and the two gossips at the ends of the telephones—may be very fascinating to a mere mathematician.
—James Clerk Maxwell (1878)
♦
A CURIOUS CHILD IN A COUNTRY TOWN
in the 1920s might naturally form an interest in the sending of messages along wires, as Claude Shannon did in Gaylord, Michigan. He saw wires every day, fencing the pastures—double strands of steel, twisted and barbed, stretched from post to post. He scrounged what parts he could and jerry-rigged his own barbed-wire telegraph, tapping messages to another boy a half mile away. He used the code devised by Samuel F. B. Morse. That suited him. He liked the very idea of codes—not just secret codes, but codes in the more general sense, words or symbols standing in for other words or symbols. He was an inventive and playful spirit. The child stayed with the man. All his life, he played games and invented games. He was a gadgeteer. The grown-up Shannon juggled and devised theories about juggling. When researchers at the Massachusetts Institute of Technology or Bell Laboratories had to leap aside to let a unicycle pass, that was Shannon. He had more than his share of playfulness, and as a child he had a large portion of loneliness, too, which along with his tinkerer’s ingenuity helped motivate his barbed-wire telegraph.
Gaylord amounted to little more than a few streets and stores interrupting the broad northern farmland of the Michigan peninsula.
♦
Here and onward across the plains and prairie to the Rocky Mountains barbed wire had spread like a vine, begetting industrial fortunes though it was not a particularly glamorous technology amid the excitement of what was already called the Age of Electricity. Beginning in 1874, when an Illinois farmer received U. S. Patent No. 157,124 for “a new and valuable Improvement in Wire-Fences,” battles for ownership raged, ultimately reaching the Supreme Court, while the wire defined territory and closed the open range. At the peak, American farmers, ranchers, and railroads laid more than a million miles a year. Taken collectively the nation’s fence wire formed no web or network, just a broken lattice. Its purpose had been to separate, not to connect. For electricity it made a poor conductor even in dry weather. But wire was wire, and Claude Shannon was not the first to see this wide-ranging lattice as a potential communications grid. Thousands of farmers in remote places had the same idea. Unwilling to wait for the telephone companies to venture out from the cities, rural folk formed barbed-wire telephone cooperatives. They replaced metal staples with insulated fasteners. They attached dry batteries and speaking tubes and added spare wire to bridge the gaps. In the summer of 1895
The New York Times
reported: “There can be no doubt that many rough-and-ready utilizations of the telephone are now being made. For instance, a number of South Dakota farmers have helped themselves to a telephone system covering eight miles of wire by supplying themselves with transmitters and making connections with the barb wire which constitutes the fence in that part of the country.” The reporter observed: “The idea is gaining ground that the day of cheap telephones for the million is at hand. Whether this impression is soundly based is an open question.”
♦
Clearly people wanted the connections. Cattlemen who despised fences for making parcels of the free range now hooked up their speaking tubes to hear market quotations, weather reports, or just, crackling along the wires, the attenuated simulacrum of the human voice, a thrill in itself.
Three great waves of electrical communication crested in sequence: telegraphy, telephony, and radio. People began to feel that it was natural to possess machines dedicated to the sending and receiving of messages. These devices changed the topology—ripped the social fabric and reconnected it, added gateways and junctions where there had only been blank distance. Already at the turn of the twentieth century there was worry about unanticipated effects on social behavior. The superintendent of the line in Wisconsin fretted about young men and women “constantly sparking over the wire” between Eau Claire and Chippewa Falls. “This free use of the line for flirtation purposes has grown to an alarming extent,” he wrote, “and if it is to go on somebody must pay for it.” The Bell companies tried to discourage frivolous telephony, particularly by women and servants. A freer spirit prevailed at the farmer cooperatives, which avoided paying the telephone companies well into the 1920s. The Montana East Line Telephone Association—eight members—sent “up to the minute” news reports around its network, because the men also owned a radio.
♦
Children wanted to play this game, too.
Claude Elwood Shannon, born in 1916, was given the full name of his father, a self-made businessman—furniture, undertaking, and real estate—and probate judge, already well into middle age. Claude’s grandfather, a farmer, had invented a machine for washing clothes: a waterproof tub, a wooden arm, and a plunger. Claude’s mother, Mabel Catherine Wolf, daughter of German immigrants, worked as a language teacher and sometime principal of the high school. His older sister, Catherine Wolf Shannon (the parents doled out names parsimoniously), studied mathematics and regularly entertained Claude with puzzles. They lived on Center Street a few blocks north of Main Street. The town of Gaylord boasted barely three thousand souls, but this was enough to support a band with Teutonic uniforms and shiny instruments, and in grade school Claude played an E-flat alto horn broader than his chest. He had Erector Sets and books. He made model planes and earned money delivering telegrams for the local Western Union office. He solved cryptograms.
Left on his own, he read and reread books; a story he loved was Edgar Allan Poe’s “The Gold-Bug,” set on a remote southern island, featuring a peculiar William Legrand, a man with an “excitable brain” and “unusual powers of mind” but “subject to perverse moods of alternate enthusiasm and melancholy”
♦
—in other words, a version of his creator. Such ingenious protagonists were required by the times and duly conjured by Poe and other prescient writers, like Arthur Conan Doyle and H. G. Wells. The hero of “The Gold-Bug” finds buried treasure by deciphering a cryptograph written on parchment. Poe spells out the string of numerals and symbols (“rudely traced, in a red tint, between the death’s-head and the goat”)—53
‡‡†
305) )6* ;4826)4
‡
.)4
‡
) ;806* ;48
†
8¶60) )85;1
‡
( ;:
‡
*8
†
83(88) 5*
‡
;46(;88*96*?;8) *
‡
(;485) ;5*
†
2:*
‡
(;4956*2(5*–4) 8§8* ;4069285) ;)6
†
8)4
‡‡
;1 (
‡
9;48081 ;8:8
‡
1 ;48
†
85;4)485
†
528806*81 (
‡
9:48;(88;4 (
‡
?34;48)4
‡
;161;:188;
‡
?;—and walks the reader through every twist of its construction and deconstruction. “Circumstances, and a certain bias of mind, have led me to take interest in such riddles,”
♦
his dark hero proclaims, thrilling a reader who might have the same bias of mind. The solution leads to the gold, but no one cares about the gold, really. The thrill is in the code: mystery and transmutation.
Claude finished Gaylord High School in three years instead of four and went on in 1932 to the University of Michigan, where he studied electrical engineering and mathematics. Just before graduating, in 1936, he saw a postcard on a bulletin board advertising a graduate-student job at the Massachusetts Institute of Technology. Vannevar Bush, then the dean of engineering, was looking for a research assistant to run a new machine with a peculiar name: the Differential Analyzer. This was a 100-ton iron platform of rotating shafts and gears. In the newspapers it was being called a “mechanical brain” or “thinking machine”; a typical headline declared:
“Thinking Machine” Does Higher Mathematics;
Solves Equations That Take Humans Months
♦
Charles Babbage’s Difference Engine and Analytical Engine loomed as ancestral ghosts, but despite the echoes of nomenclature and the similarity of purpose, the Differential Analyzer owed virtually nothing to Babbage. Bush had barely heard of him. Bush, like Babbage, hated the numbing, wasteful labor of mere calculation. “A mathematician is not a man who can readily manipulate figures; often he cannot,” Bush wrote. “He is primarily an individual who is skilled in the use of symbolic logic on a high plane, and especially he is a man of intuitive judgment.”
♦
MIT in the years after World War I was one of the nation’s three focal points for the burgeoning practical science of electrical engineering, along with the Bell Telephone Laboratories and General Electric. It was also a place with a voracious need for the solving of equations—especially differential equations, and particularly differential equations of the second order. Differential equations express rates of change, as in ballistic projectiles and oscillating electric currents. Second-order differential equations concern rates of change in rates of change: from position to velocity to acceleration. They are hard to solve analytically, and they pop up everywhere. Bush designed his machine to handle this entire class of problems and thus the whole range of physical systems that generated them. Like Babbage’s machines, it was essentially mechanical, though it used electric motors to drive the weighty apparatus and, as it evolved, more and more electromechanical switches to control it.
Unlike Babbage’s machine, it did not manipulate numbers. It worked on quantities—generating curves, as Bush liked to say, to represent the future of a dynamical system. We would say now that it was analog rather than digital. Its wheels and disks were arranged to produce a physical analog of the differential equations. In a way it was a monstrous descendant of the planimeter, a little measuring contraption that translated the integration of curves into the motion of a wheel. Professors and students came to the Differential Analyzer as supplicants, and when it could solve their equations with 2 percent accuracy, the operator, Claude Shannon, was happy. In any case he was utterly captivated by this “computer,” and
not just by the grinding, rasping, room-filling analog part, but by the nearly silent (save for the occasional click and tap) electrical controls.
♦
