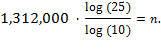The Unimaginable Mathematics of Borges' Library of Babel (8 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction
gggggggggggggggggggggggggggggggggggggggghggggggggggggggggggggggggggggggggggggggg
and, as above, all of the rest
of the symbols in the book are the letter
g
.
How many
books like this are there? Well, there are exactly 1,312,000 different slots
that the single
h
can occupy, and every other slot must be filled with a
g
. Thus, there are exactly 1,312,000 such books.
Now, we
allow ourselves to imagine a book that consists of 1,311,998 slots filled with
the symbol
g
and two slots—not necessarily adjacent— filled with an
h.
There are precisely
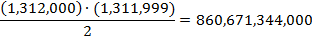
such books. (At the end of
this chapter, see the second Math Aftermath, "An Example of the Ars
Combinatoria," for an explanation of this and the next two formulas.) Put
into human terms, assuming the world population is currently somewhat less than
seven billion people, this translates to every one of us enjoying a personal
library of about 123 of these books.
If we next
consider books that, excepting three instances of the letter h, are all g, all
the time, we perform a similar calculation to find that there are exactly
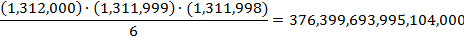
such books. This number,
although perhaps not appearing much larger than the preceding one, expands
these monotonous libraries to about 53 million distinct books for each person
currently alive.
Pursuing
this notion to its conclusion, by considering the number of books consisting of
a mere 16 occurrences of the letter
h
in an otherwise uniform desert of
the letter
g
, we find there are
3,683,681,259,485,362,310,918,865,543,989,208,654,728,931,149,486,911,733,618,072,454,576,141,229,488,660,718,000
distinct books—about 3.7 x 10
84
books—more than enough to fill three cubic universes. These books, droning
wearily of
g
with a little respite provided only by the scant 16
instances of
h
, are not typographical phantasmagoria to inflame the
imagination or addle the senses, and yet if they were all collected into a
subsection of the Library, they would occupy a space greater than three times
our known universe.
Finally, it
would be a tedious, uninspired, but straightforward calculation to determine
how big the Library needs be to hold the books in the hexagonal configurations
described by Borges. Given the work we've just done, it should be clear that
however the Library is constructed, any sort of ambulatory circumnavigation
would be utterly impossible for a human being: a vigorous, long-lived librarian
who managed to walk a little over 60 miles—about 100 kilometers—every day for
100 years would cover somewhat less distance than light travels in two
minutes.
To cross our universe, which is incomprehensibly dwarfed by the
Library, light would need to travel for at least 15 billion
years.
The
number of books in the Library, although easily notated, is unimaginable.
Math Aftermath I: The Logos of Logarithms
There are those who dance
to the rhythm that is played to them, those who only dance to their own rhythm,
and those who don't dance at all.
—Jose
Bergamin,
The Rocket and the Star
This Aftermath is included for
two purposes, one explanatory and one hortatory. The expository side is to
provide a basis for those who wish to understand the details of how certain
approximations and calculations are made in this chapter, as well as the
chapter "Real Analysis." The public relations portion is to
reconceive of the logarithm as a function imbued with a friendly collection of
useful, easily manipulated properties.
For the
purposes of this book, we'll say that
a function
is a rule such that for
each legitimate number the rule is applied to, it returns back exactly one
number. The output number might be the same or different from the input number;
however, the important thing is that given a specific input number, the output
number for it is always the same. (There are many interesting generalizations
of this idea, including that of studying spaces whose elements are themselves
functions.) One of the functions most misunderstood and maligned by generations
of students is that of the logarithm.
The
logarithm (base 10) is typically notated
log
; frequently it is written
log(x)
to emphasize it is a function: given an input of one number,
x,
it outputs another number,
log(x).
The modern notation is quite
evocative:
x
→
log(x).
We could, at this juncture,
include a graph of the logarithmic function; after all, a picture is useful for
nurturing our visual awareness. However, we deliberately exclude such an
illustration to hammer home a point: the logarithm, as it turns out, is a
function that may be defined by a number of truly remarkable properties. Since
really we only need to use one of the properties, let's jump right in: if
x
is any positive number, and
n
is any number, then
log(x
n
)
=
n log(x).
log(x).
That is, the logarithm,
remarkably, "lowers" the exponential, thereby reducing it to a much
more familiar operation—multiplication. There are many marvelous implications
of this property, but for our purposes, the property alone will give us what we
need.
Earlier in
the chapter, using exponential notation, we found that there are 25
1,312,000
distinct volumes in
the Library. We'd like to contextualize the number of books by putting that
number into a somewhat more familiar form. We choose to convert it to the power
of 10 notation, 10
n
, because we may think of that as a single 1
followed by
n
0s. Therefore, we set up the following equation and
endeavor to solve it for
n
.
25
1,312,000
= 10
n
When we solve this equation
for
n,
we thus gain a greater intuition for the number of books in the
Library.
Here's the
key point: even though 25
1,312,000
and 10
n
are written
differently and look different, if we choose some
n
such that the two
numbers are equal,
then they are, in fact, the same number.
Since they
are the same number, by the definition of a function, it must the case that
using both representations of the number as inputs to the function entails that
both of the outputs must continue to be equal to each other. So we apply the
logarithm to both sides of the equation and get
log
(25
1,312,000
) =
log
(10
n
).
Now, the remarkable property
of the logarithm "brings the exponential down" and gives
1,312,000 log
log
(25) = n log
log
(10).
(In fact, things are even
better than they appear, for
log
(10) is equal to 1, but that need not concern us here.) Divide
both sides by
log
(10) to
solve for
n
: