Understanding Computation (12 page)
DFAs are simple to
understand and to implement, but that’s because they’re very
similar to machines we’re already familiar with. Having stripped away all
the complexity of a real computer, we now have the opportunity to
experiment with less conventional ideas that take us further away from the
machines we’re used to, without having to deal with the incidental
difficulties of making those ideas work in a real system.
One way to explore is by chipping away at our existing assumptions
and constraints. For one thing, the determinism constraints seem
restrictive: maybe we don’t care about every possible input character at
every state, so why can’t we just leave out rules for characters we don’t
care about and assume that the machine can go into a generic failure state
when something unexpected happens? More exotically, what would it mean to
allow the machine to have contradictory rules, so that more than one
execution path is possible? Our setup also assumes that each state change
must happen in response to a character being read from the input stream,
but what would happen if the machine could change state without having to
read anything?
In this section, we’ll investigate these ideas and see what new possibilities are opened
up by tweaking a finite automaton’s capabilities.
Suppose we
wanted a finite automaton that would accept any string ofas andbs as long as the third character wasb. It’s easy enough to come up with a suitable
DFA design:
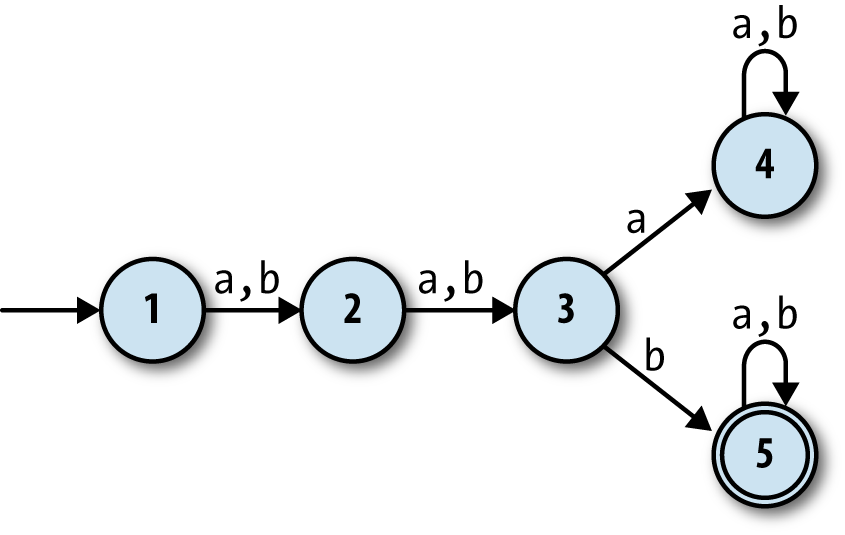
What if we wanted a machine that would accept strings where the
third-from-last
character isb? How would that work? It seems more
difficult: the DFA above is guaranteed to be in state 3 when it reads
the third character, but a machine can’t know in advance
when
it’s reading the third-from-last character,
because it doesn’t know how long the string is until it’s finished
reading it. It might not be immediately clear whether such a DFA is even
possible.
However, if we relax the determinism constraints and allow the
rulebook to contain multiple rules (or no rules at all)
for a given state and input, we can design a machine that does the
job:
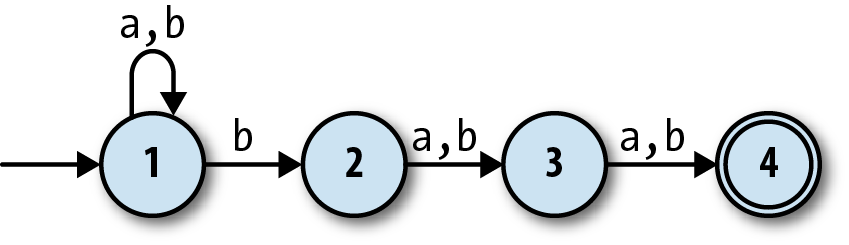
This state machine, a
nondeterministic finite
automaton
(NFA), no longer has exactly one execution path
for each sequence of
inputs. When it’s in state 1 and readsbas input, it’s possible for it to follow a
rule that keeps it in
state 1, but it’s also possible for it to follow a
different rule that takes it into state 2 instead. Conversely, once it
gets into state 4, it has no rules to follow and therefore no way to
read any more input. A DFA’s next state is always completely determined
by its current state and its input, but an NFA sometimes has more than
one possibility for which state to move into next, and sometimes none at
all.
A DFA accepts a string if reading the characters and blindly
following the rules causes the machine to end up in an accept state, so
what does it mean for an NFA to accept or reject a string? The natural
answer is that a string is accepted if there’s
some
way for the NFA to end up in an accept state by following some of its
rules—that is, if finishing in an accept state is
possible
, even if it’s not inevitable.
For example, this NFA accepts the string'baa',
because,
starting at state 1, the rules say there is a way for the machine to read aband move into state 2, then read anaand move into state 3, and finally read anotheraand finish in state 4, which is an accept state. It also
accepts the string'bbbbb', because it’s possible for the
NFA to initially follow a different rule and stay in state 1 while reading the first twobs, and only use the rule for moving into state 2 when
reading the thirdb, which then lets it read the rest of
the string and finish in state 4 as before.
On the other hand, there’s no way for it to read'abb'and end up in state 4—depending on which rules it follows, it can only
end up in state 1, 2, or 3—so'abb'is not accepted by
this NFA. Neither is'bbabb', which can only ever get as
far as state 3; if it goes straight into state 2 when reading the firstb, it will end up in state 4 too early, with two characters
still left to read but no more
rules to follow.
The collection of strings that are accepted by a particular
machine is called a
language
: we say that the
machine
recognizes
that language. Not all
possible languages have a DFA or NFA that can recognize them (see
Chapter 4
for more information), but those
languages that can be recognized by finite automata are called
regular languages
.
Relaxing the determinism constraints has produced an imaginary
machine that is very different from the real, deterministic computers
we’re familiar with. An NFA deals in possibilities rather than
certainties; we talk about its behavior in terms of what
can
happen rather than what
will
happen. This seems powerful, but how can such
a machine work in the real world? At first glance it looks like a real
implementation of an NFA would need some kind of foresight in order to
know which of several possibilities to choose while it reads input: to
stand a chance of accepting a string, our example NFA must stay in state
1 until it reads the third-from-last character, but it has no way of
knowing how many more characters it will receive. How can we simulate an
exciting machine like this in boring, deterministic Ruby?
The key to
simulating an NFA on a deterministic computer is to find a way to explore
all possible executions
of the machine. This brute-force approach
eliminates the spooky foresight that would be required to simulate only one possible
execution by somehow making all the right decisions along the way. When an NFA reads a
character, there are only ever a finite number of possibilities for what it can do next, so
we can simulate the nondeterminism by somehow trying all of them and seeing whether any of
them ultimately allows it to reach an accept state.
We could do this by recursively trying all possibilities: each time the simulated NFA
reads a character and there’s more than one applicable rule, follow one of those rules and
try reading the rest of the input; if that doesn’t leave the machine in an accept state,
then go back into the earlier state, rewind the input to its earlier position, and try again
by following a different rule; repeat until some choice of rules leads to an accept state,
or until all possible choices have been tried without success.
Another strategy is to simulate all possibilities in parallel by spawning new threads
every time the machine has more than one rule it can follow next, effectively copying the
simulated NFA so that each copy can try a different rule to see how it pans out. All those
threads can be run at once, each reading from its own copy of the input string, and if any
thread ends up with a machine that’s read every character and stopped in an accept state,
then we can say the string has been accepted.
Both of these implementations are feasible, but they’re a bit
complicated and inefficient. Our DFA simulation was simple and could
read individual characters while constantly reporting back on whether
the machine is in an accept state, so it would be nice to simulate an
NFA in a way that gives us the same simplicity and transparency.
Fortunately, there’s an easy way to simulate an NFA without needing to rewind our
progress, spawn threads, or know all the input characters in advance. In fact, just as we
simulated a single DFA by keeping track of its current state, we can simulate a single NFA
by keeping track of all its
possible
current states. This is simpler
and more efficient than simulating multiple NFAs that go off in different directions, and it
turns out to achieve the same thing in the end. If we did simulate many separate machines,
then all we’d care about is what state each of them was in, but any machines in the same
state are completely indistinguishable,
[
21
]
so we don’t lose anything by collapsing all those possibilities down into a
single machine and asking “which states
could
it be in by now?”
instead.
For example, let’s walk through what happens to our example NFA as it reads the string'bab':
Before the NFA has read any input, it’s definitely in state 1, its start
state.It reads the first character,
b. From state 1,
there’s onebrule that lets the NFA stay in state 1
and anotherbrule that takes it to state 2, so we
know it can be in either state 1 or 2 afterward. Neither of those is an accept state,
which tells us there’s no possible way for the NFA to reach an accept state by reading
the string'b'.It reads the second character,
a. If it’s in
state 1 then there’s only onearule it can follow,
which will keep it in state 1; if it’s in state 2, it’ll have to follow thearule that leads to state 3. It must end up in state 1 or
3, and again, these aren’t accept states, so there’s no way the string'ba'can be accepted by this machine.It reads the third character,
b. If it’s in state
1 then, as before it can stay in state 1 or go to state 2; if it’s in state 3, then it
must go to state 4.Now we know that it’s possible for the NFA to be in state 1, state 2, or state 4
after reading the whole input string. State 4
is
an accept state,
and our simulation shows that there must be
some
way for the
machine to reach state 4 by reading that string, so the NFA
does
accept'bab'.
This simulation strategy is easy to turn into code. First we need
a rulebook suitable for
storing an NFA’s rules. A DFA rulebook always returns a
single state when we ask it where the DFA should go next after reading a
particular character while in a specific state, but an NFA rulebook
needs to answer a different question: when an NFA is possibly in one of
several states, and it reads a particular character, what states can it
possibly be in next? The implementation looks like this:
require'set'classNFARulebook<Struct.new(:rules)defnext_states(states,character)states.flat_map{|state|follow_rules_for(state,character)}.to_setenddeffollow_rules_for(state,character)rules_for(state,character).map(&:follow)enddefrules_for(state,character)rules.select{|rule|rule.applies_to?(state,character)}endend
We’re using theSetclass,
from Ruby’s standard library, to store the collection of possible
states returned by#next_states. We
could have used anArray, butSethas three useful
features:
It automatically eliminates duplicate elements.
Set[1, 2, 2, 3, 3, 3]is equal toSet[1, 2, 3].It ignores the order of elements.
Set[3, 2, 1]is equal toSet[1, 2, 3].It provides standard set operations like intersection
(#&), union (#+), and subset testing (#subset?).
The first feature is useful because it doesn’t make sense to say
“the NFA is in state 3 or state 3,” and returning aSetmakes sure we never include any
duplicates. The other two features will be useful later.