Understanding Computation (14 page)
We’ve seen that
nondeterminism and free moves make finite automata more expressive without
interfering with our ability to simulate them. In this section, we’ll look at an important
practical application of these features: regular expression matching.
Regular expressions
provide
a language for writing textual
patterns
against which strings may be matched. Some
example regular expressions are:
hello, which only matches the string'hello'hello|goodbye, which matches the strings'hello'and'goodbye'(hello)*, which matches the strings'hello','hellohello','hellohellohello', and so on, as well as the empty
string
In this chapter, we’ll always think of a regular expression as matching an
entire
string. Real-world implementations of regular expressions
typically use them for matching
parts
of strings, with extra syntax
needed if we want to specify that an entire string should be matched.
For example, our regular expressionhello|goodbyewould be written in Ruby as/\A(hello|goodbye)\z/to make sure
that any match is anchored to the beginning (\A) and end (\z) of the string.
Given a regular expression and a string, how do we write a program
to decide whether the string matches that expression? Most programming
languages, Ruby included, already have regular expression support built
in, but how does that support work? How would we implement regular
expressions in Ruby if the language didn’t already have them?
It turns out that finite automata are perfectly suited to this job. As we’ll see, it’s
possible to convert any regular expression into an equivalent NFA—every string matched by the
regular expression is accepted by the NFA, and vice versa—and then match a string by feeding
it to a simulation of that NFA to see whether it gets accepted. In the language of
Chapter 2
, we can think of this as providing a sort of
denotational semantics for regular expressions: we may not know how to execute a regular
expression directly, but we can show how to denote it as an NFA, and because we have an
operational semantics for NFAs (“change state by reading characters and following rules”), we
can execute the denotation to achieve the same result.
Let’s be precise
about what we mean by “regular expression.” To get us off
the ground, here are two kinds of extremely simple regular expression
that are not built out of anything simpler:
An empty regular expression. This matches the empty string and
nothing else.A regular expression containing a single, literal character. For example,
aandbare regular
expressions that match only the strings'a'and'b'respectively.
Once we have these simple kinds of pattern, there are three ways
we can combine them to build more complex expressions:
Concatenate two patterns. We can concatenate the regular expressions
aandbto get the
regular expressionab, which only matches the string'ab'.Choose between two patterns, written by joining them with the
|operator. We can join the regular expressionsaorbto get the regular
expressiona|b, which matches the strings'a'and'b'.Repeat a pattern zero or more times, written by suffixing it with the
*operator. We can suffix the regular expressionato geta*, which
matches the strings'a','aa','aaa', and so on, as well as the
empty string''(i.e., zero repetitions).
Real-world regular expression engines, like the one built into Ruby, support more
features than this. In the interests of simplicity, we won’t try to implement these extra
features, many of which are technically redundant and only provided as a
convenience.
For example, omitting the repetition operators?and+doesn’t make an important difference, because
their effects—“repeat one or zero times” and “repeat one or more times,” respectively—are
easy enough to achieve with the features we already have: the regular expressionab?can be rewritten asab|a, and the patternab+matches the same
strings asabb*. The same is true of other convenience
features like counted repetition (e.g.,a{2,5}) and
character classes (e.g.,[abc]).
More advanced features like capture groups, backreferences and
lookahead/lookbehind assertions are outside of the scope of this
chapter.
To implement this syntax in Ruby, we can define a class for each kind of regular
expression and use instances of those classes to represent the abstract syntax tree of any
regular expression, just as we did for
Simple
expressions
in
Chapter 2
:
modulePatterndefbracket(outer_precedence)ifprecedence<outer_precedence'('+to_s+')'elseto_sendenddefinspect"/#{self}/"endendclassEmptyincludePatterndefto_s''enddefprecedence3endendclassLiteral<Struct.new(:character)includePatterndefto_scharacterenddefprecedence3endendclassConcatenate<Struct.new(:first,:second)includePatterndefto_s[first,second].map{|pattern|pattern.bracket(precedence)}.joinenddefprecedence1endendclassChoose<Struct.new(:first,:second)includePatterndefto_s[first,second].map{|pattern|pattern.bracket(precedence)}.join('|')enddefprecedence0endendclassRepeat<Struct.new(:pattern)includePatterndefto_spattern.bracket(precedence)+'*'enddefprecedence2endend
In the same way that multiplication binds its arguments more tightly than addition in
arithmetic expressions (1 + 2 × 3 equals 7, not 9), the convention for the concrete syntax
of regular expressions is for the*operator to bind
more tightly than concatenation, which in turn binds more tightly than the|operator. For example, in the regular expressionabc*it’s understood that the*applies only to thec('abc','abcc','abccc'…), and to make it apply to all ofabc('abc','abcabc'…), we’d need to add brackets and write(abc)*instead.
The syntax classes’ implementations of#to_s, along with thePattern#bracketmethod, deal with
automatically inserting these brackets when necessary so that we can
view a simple string representation of an abstract syntax tree without
losing information about its structure.
These classes let us
manually build trees to represent regular
expressions:
>>pattern=Repeat.new(Choose.new(Concatenate.new(Literal.new('a'),Literal.new('b')),Literal.new('a')))=> /(ab|a)*/
Of course, in a real implementation, we’d use a parser to build these trees instead of
constructing them by hand; see
Parsing
for instructions
on how to do
this.
Now that we
have a way of representing the syntax of a regular
expression as a tree of Ruby objects, how can we convert that syntax
into an NFA?
We need to decide how instances of each syntax class should be
turned into NFAs. The easiest class to convert isEmpty, which we should always turn into the
one-state NFA that only accepts the empty string:

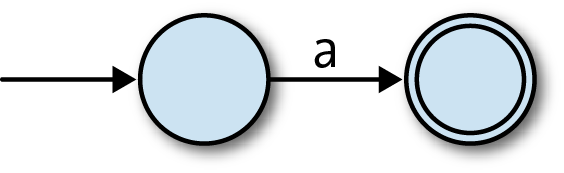
Similarly, we should turn any literal, single-character pattern
into the NFA that only accepts the single-character string containing
that character. Here’s the NFA for the patterna:
It’s easy enough to implement#to_nfa_designmethods forEmptyandLiteralto generate these NFAs:
classEmptydefto_nfa_designstart_state=Object.newaccept_states=[start_state]rulebook=NFARulebook.new([])NFADesign.new(start_state,accept_states,rulebook)endendclassLiteraldefto_nfa_designstart_state=Object.newaccept_state=Object.newrule=FARule.new(start_state,character,accept_state)rulebook=NFARulebook.new([rule])NFADesign.new(start_state,[accept_state],rulebook)endend
As mentioned in
Simulation
, the states of an automaton must be
implemented as Ruby objects that can be distinguished from each other. Here, instead of
using numbers (i.e.,Fixnuminstances) as states, we’re
using freshly created instances ofObject.
This is so that each NFA gets its own unique states, which gives
us the ability to combine small machines into larger ones without
accidentally merging any of their states. If two distinct NFAs both
used the RubyFixnumobject1as a state, for example, they
couldn’t be connected together while keeping those two states
separate. We’ll want to be able to do that as part of implementing
more complex regular expressions.
Similarly, we won’t label states on the diagrams any more, so
that we don’t have to relabel them when we start connecting diagrams
together.
We can check that the
NFAs generated fromEmptyandLiteralregular expressions accept the strings
we want them to:
>>nfa_design=Empty.new.to_nfa_design=> #>>nfa_design.accepts?('')=> true>>nfa_design.accepts?('a')=> false>>nfa_design=Literal.new('a').to_nfa_design=> #>>nfa_design.accepts?('')=> false>>nfa_design.accepts?('a')=> true>>nfa_design.accepts?('b')=> false
There’s an opportunity here to wrap#to_nfa_designin a#matches?method to give patterns a nicer
interface:
modulePatterndefmatches?(string)to_nfa_design.accepts?(string)endend
This lets us match patterns directly against strings:
>>Empty.new.matches?('a')=> false>>Literal.new('a').matches?('a')=> true
Now that we know how to turn simpleEmptyandLiteralregular expressions into NFAs, we need
a similar setup forConcatenate,Choose, andRepeat.
Let’s begin withConcatenate:
if we have two regular expressions that we already know how to turn into
NFAs, how can we build an NFA to represent the concatenation of those
regular expressions? For example, given that we can turn
the single-character regular expressionsaandbinto NFAs, how do we turnabinto
one?
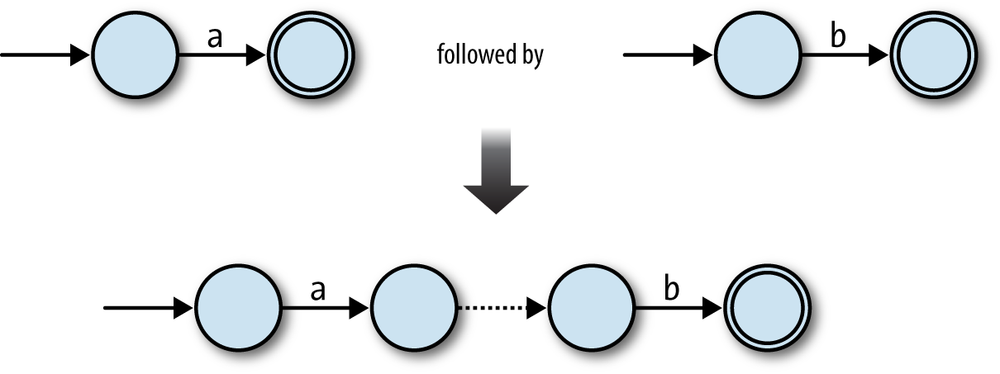
In theabcase, we can connect the two NFAs in
sequence, joining them together with a free move, and keeping the second NFA’s accept
state:
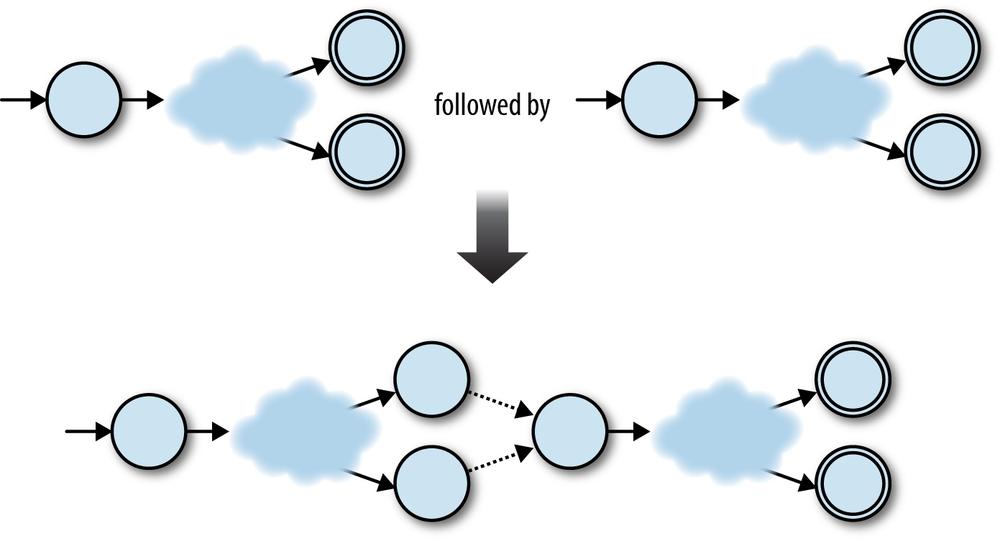
This technique works in other cases too. Any two NFAs can be concatenated by turning
every accept state from the first NFA into a nonaccept state and connecting it to the start
state of the second NFA with a free move. Once the concatenated machine has read a sequence
of inputs that would have put the first NFA into an accept state, it can spontaneously move
into a state corresponding to the start state of the second NFA, and then reach an accept
state by reading a sequence of inputs that the second NFA would have accepted.
So, the raw ingredients for the combined machine are:
The start state of the first NFA
The accept states of the second NFA
All the rules from both NFAs
Some extra free moves to connect each of the first NFA’s old accept states to the
second NFA’s old start state
We can turn this idea into an implementation ofConcatenate#to_nfa_design:
classConcatenatedefto_nfa_designfirst_nfa_design=first.to_nfa_designsecond_nfa_design=second.to_nfa_designstart_state=first_nfa_design.start_stateaccept_states=second_nfa_design.accept_statesrules=first_nfa_design.rulebook.rules+second_nfa_design.rulebook.rulesextra_rules=first_nfa_design.accept_states.map{|state|FARule.new(state,nil,second_nfa_design.start_state)}rulebook=NFARulebook.new(rules+extra_rules)NFADesign.new(start_state,accept_states,rulebook)endend
This code first converts the first and second regular expressions
intoNFADesigns, then combines their
states and rules in the appropriate way to make a newNFADesign. It works as expected for the simpleabcase: