Antifragile: Things That Gain from Disorder (56 page)
Read Antifragile: Things That Gain from Disorder Online
Authors: Nassim Nicholas Taleb
And now, reader, after the Herculean effort I put into making the ideas of the last few chapters clearer to you, my turn to take it easy and express things technically, sort of. Accordingly, this chapter—a deepening of the ideas of the previous one—will be denser and should be skipped by the enlightened reader.
Let us examine a method to detect fragility—the inverse philosopher’s stone. We can illustrate it with the story of the giant government-sponsored lending firm called Fannie Mae, a corporation that collapsed leaving the United States taxpayer with hundreds of billions of dollars of losses (and, alas, still counting).
One day in 2003, Alex Berenson, a
New York Times
journalist, came into my office with the secret risk reports of Fannie Mae, given to him by a defector. It was the kind of report getting into the guts of the methodology for risk calculation that only an insider can see—Fannie Mae made its own risk calculations and disclosed what it wanted to whomever it wanted, the public or someone else. But only a defector could show us the guts to see how the risk was calculated.
We looked at the report: simply, a move upward in an economic variable led to massive losses, a move downward (in the opposite direction), to small profits. Further moves upward led to even larger additional losses and further moves downward to even smaller profits. It looked exactly like the story of the stone in
Figure 9
. Acceleration of harm was obvious—in fact it was monstrous. So we immediately saw that their blowup was inevitable: their exposures were severely “concave,” similar to the graph of traffic in
Figure 14
: losses that accelerate as one deviates economic variables (I did not even need to understand which one, as fragility to one variable of this magnitude implies fragility to all other parameters). I worked with my emotions, not my brain, and I had a pang before even understanding what numbers I had been looking at. It was the mother of all fragilities and, thanks to Berenson,
The New York Times
presented my concern. A smear campaign ensued, but nothing too notable. For I had in the meantime called a few key people charlatans and they were not too excited about it.
The key is that the nonlinear is vastly more affected by extreme events—and nobody was interested in extreme events since they had a mental block against them.
I kept telling anyone who would listen to me, including random taxi drivers (well, almost), that the company Fannie Mae was “sitting on a barrel of dynamite.” Of course, blowups don’t happen every day (just as poorly built bridges don’t collapse immediately), and people kept saying that my opinion was wrong and unfounded (using some argument that the stock was going up or something even more circular). I also inferred that other institutions, almost all banks, were in the same situation. After checking similar institutions, and seeing that the problem was general, I realized that a total collapse of the banking system was a certainty. I was so certain I could not see straight and went back to the markets to get my revenge against the turkeys. As in the scene from
The Godfather
(III), “Just when I thought I was out, they pull me back in.”
Things happened as if they were planned by destiny. Fannie Mae went bust, along with other banks. It just took a bit longer than expected, no big deal.
The stupid part of the story is that I had not seen the link between financial and general fragility—nor did I use the term “fragility.” Maybe I didn’t look at too many porcelain cups. However, thanks to the episode of the attic I had a measure for fragility, hence antifragility.
It all boils down to the following: figuring out if our miscalculations
or misforecasts are on balance more harmful than they are beneficial, and how accelerating the damage is. Exactly as in the story of the king, in which the damage from a ten-kilogram stone is more than twice the damage from a five-kilogram one. Such accelerating damage means that a large stone would eventually kill the person. Likewise a large market deviation would eventually kill the company.
Once I figured out that fragility was directly from nonlinearity and convexity effects, and that convexity was measurable, I got all excited. The technique—detecting
acceleration
of harm—applies to anything that entails decision making under uncertainty, and risk management. While it was the most interesting in medicine and technology, the immediate demand was in economics. So I suggested to the International Monetary Fund a measure of fragility to substitute for their measures of risk that they knew didn’t work. Most people in the risk business had been frustrated by the poor (rather, the random) performance of their models, but they didn’t like my earlier stance: “don’t use any model.” They wanted something. And a risk measure was there.
1
So here is something to use. The technique, a simple heuristic called the
fragility (and antifragility) detection heuristic,
works as follows. Let’s say you want to check whether a town is overoptimized. Say you measure that when traffic increases by ten thousand cars, travel time grows by ten minutes. But if traffic increases by ten thousand more cars, travel time now extends by an extra thirty minutes. Such acceleration of traffic time shows that traffic is fragile and you have too many cars and need to reduce traffic until the acceleration becomes mild (acceleration, I repeat, is acute concavity, or negative convexity effect).
Likewise, government deficits are particularly concave to changes in economic conditions. Every additional deviation in, say, the unemployment rate—particularly when the government has debt—makes deficits incrementally worse. And financial leverage for a company has the same
effect: you need to borrow more and more to get the same effect. Just as in a Ponzi scheme.
The same with operational leverage on the part of a fragile company. Should sales increase 10 percent, then profits would increase less than they would decrease should sales drop 10 percent.
That was in a way the technique I used intuitively to declare that the Highly Respected Firm Fannie Mae was on its way to the cemetery—and it was easy to produce a rule of thumb out of it. Now with the IMF we had a simple measure with a stamp. It looks simple, too simple, so the initial reaction from “experts” was that it was “trivial” (said by people who visibly never detected these risks before—academics and quantitative analysts scorn what they can understand too easily and get ticked off by what they did not think of themselves).
According to the wonderful principle that one should use people’s stupidity to have fun, I invited my friend Raphael Douady to collaborate in expressing this simple idea using the most opaque mathematical derivations, with incomprehensible theorems that would take half a day (for a professional) to understand. Raphael, Bruno Dupire, and I had been involved in an almost two-decades-long continuous conversation on how everything entailing risk—everything—can be seen with a lot more rigor and clarity from the vantage point of an option professional. Raphael and I managed to prove the link between nonlinearity, dislike of volatility, and fragility. Remarkably—as has been shown—if you can say something straightforward in a complicated manner with complex theorems, even if there is no large gain in rigor from these complicated equations, people take the idea very seriously. We got nothing but positive reactions, and we were now told that this simple detection heuristic was “intelligent” (by the same people who had found it trivial). The only problem is that mathematics is addictive.
Now what I believe is my true specialty: error in models.
When I was in the transaction business, I used to make plenty of errors of execution. You buy one thousand units and in fact you discover the next day that you bought two thousand. If the price went up in the meantime you had a handsome profit. Otherwise you had a large loss. So these errors are in the long run neutral in effect, since they can affect you both ways. They increase the variance, but they don’t affect your
business too much. There is no one-sidedness to them. And these errors can be kept under control thanks to size limits—you make a lot of small transactions, so errors remain small. And at year end, typically, the errors “wash out,” as they say.
But that is not the case with most things we build, and with errors related to things that are fragile, in the presence of negative convexity effects. This class of errors has a one-way outcome, that is, negative, and tends to make planes land later, not earlier. Wars tend to get worse, not better. As we saw with traffic, variations (now called disturbances) tend to increase travel time from South Kensington to Piccadilly Circus, never shorten it. Some things, like traffic, do rarely experience the equivalent of positive disturbances.
This one-sidedness brings both underestimation of randomness and underestimation of harm, since one is more exposed to harm than benefit from error. If in the long run we get as much variation in the source of randomness one way as the other, the harm would severely outweigh the benefits.
So—and this is the key to the Triad—we can classify things by three simple distinctions: things that, in the long run, like disturbances (or errors), things that are neutral to them, and those that dislike them. By now we have seen that evolution likes disturbances. We saw that discovery likes disturbances. Some forecasts are hurt by uncertainty—and, like travel time, one needs a buffer. Airlines figured out how to do it, but not governments, when they estimate deficits.
This method is very general. I even used it with Fukushima-style computations and realized how fragile their computation of small probabilities was—in fact all small probabilities tend to be very fragile to errors, as a small change in the assumptions can make the probability rise dramatically, from one per million to one per hundred. Indeed, a ten-thousand-fold underestimation.
Finally, this method can show us where the math in economic models is bogus—which models are fragile and which ones are not. Simply do a small change in the assumptions, and look at how large the effect, and if there is acceleration of such effect. Acceleration implies—as with Fannie Mae—that someone relying on the model blows up from Black Swan effects.
Molto facile.
A detailed methodology to detect which results are bogus in economics—along with a discussion of small probabilities—is provided in the Appendix. What I can say for now is that much of what
is taught in economics that has an equation, as well as econometrics, should be immediately ditched—which explains why economics is largely a charlatanic profession. Fragilistas,
semper fragilisti
!
Next I will explain the following effect of nonlinearity: conditions under which the average—the first order effect—does not matter. As a first step before getting into the workings of the philosopher’s stone.
As the saying goes:
Do not cross a river if it is on average four feet deep.
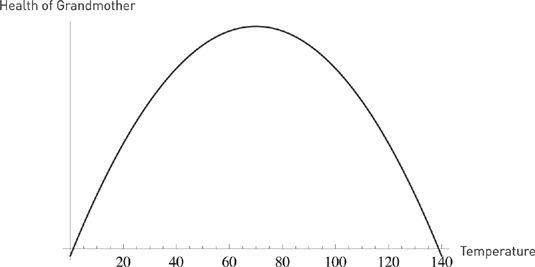
You have just been informed that your grandmother will spend the next two hours at the very desirable average temperature of seventy degrees Fahrenheit (about twenty-one degrees Celsius). Excellent, you think, since seventy degrees is the optimal temperature for grandmothers. Since you went to business school, you are a “big picture” type of person and are satisfied with the summary information.
But there is a second piece of data. Your grandmother, it turns out, will spend the first hour at zero degrees Fahrenheit (around minus eighteen Celsius), and the second hour at one hundred and forty degrees (around 60º C), for an average of the very desirable Mediterranean-style seventy degrees (21º C). So it looks as though you will most certainly end up with no grandmother, a funeral, and, possibly, an inheritance.
Clearly, temperature changes become more and more harmful as they deviate from seventy degrees. As you see, the second piece of information, the variability, turned out to be more important than the first. The notion of average is of no significance when one is fragile to variations—the dispersion in possible thermal outcomes here matters much more. Your grandmother is fragile to variations of temperature, to the volatility of the weather. Let us call that second piece of information the
second-order effect,
or, more precisely, the
convexity effect
.
Here, consider that, as much as a good simplification the notion of average can be, it can also be a Procrustean bed. The information that the average temperature is seventy degrees Fahrenheit does not simplify the situation for your grandmother. It is information squeezed into a Procrustean bed—and these are necessarily committed by scientific modelers,
since a model is
by its very nature
a simplification. You just don’t want the simplification to distort the situation to the point of being harmful.
Figure 16
shows the fragility of the health of the grandmother to variations. If I plot health on the vertical axis, and temperature on the horizontal one, I see a shape that curves inward—a “concave” shape, or
negative
convexity effect.
If the grandmother’s response was “linear” (no curve, a straight line), then the harm of temperature below seventy degrees would be offset by the benefits of temperature above it. And the fact is that the health of the grandmother has to be capped at a maximum, otherwise she would keep improving.
FIGURE 16
. Megafragility. Health as a function of temperature curves inward. A combination of 0 and 140 degrees (F) is worse for your grandmother’s health than just 70 degrees. In fact almost
any
combination averaging 70 degrees is worse than just 70 degrees.
2
The graph shows concavity or negative convexity effects—curves inward.