Data Mining (123 page)
Authors: Mehmed Kantardzic
where
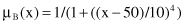
This is illustrated in Figure
14.1
b.
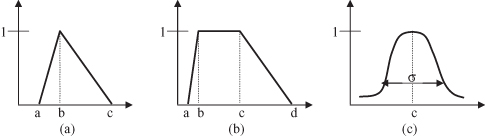
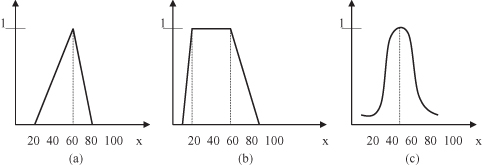
As mentioned earlier, a fuzzy set is completely characterized by its MF. Since many fuzzy sets in use have a universe of discourse X consisting of the real line R, it would be impractical to list all the pairs defining an MF. A more convenient and concise way to define an MF is to express it as a mathematical formula. Several classes of parametrized MFs are introduced, and in real-world applications of fuzzy sets the shape of MFs is usually restricted to a certain class of functions that can be specified with only few parameters. The most well known are triangular, trapezoidal, and Gaussian; Figure
14.2
shows these commonly used shapes for MFs.
Figure 14.2.
Most commonly used shapes for membership functions. (a) Triangular; (b) trapezoidal; (c) Gaussian.
A triangular MF is specified by three parameters {a, b, c} as follows:
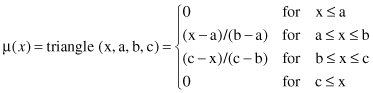
The parameters {a, b, c}, with a < b < c, determine the x coordinates of the three corners of the underlying triangular MF.
A trapezoidal MF is specified by four parameters {a, b, c, d} as follows:
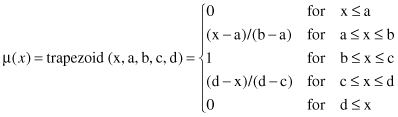
The parameters {a, b, c, d}, with a < b ≤ c < d, determine the x coordinates of the four corners of the underlying trapezoidal MF. A triangular MF can be seen as a special case of the trapezoidal form where b = c.
Finally, a Gaussian MF is specified by two parameters {c, σ}:
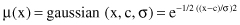
A Gaussian MF is determined completely by c and σ; c represents the membership-function center, and σ determines the membership-function width. Figure
14.3
illustrates the three classes of parametrized MFs.
Figure 14.3.
Examples of parametrized membership functions. (a) Triangle(x, 20, 60, 80); (b) trapezoid(x, 10, 20, 60, 90); (c) Gaussian(x, 50, 20).
From the preceding examples, it is obvious that the construction of a fuzzy set depends on two things: the identification of a suitable universe of discourse and the specification of an appropriate MF. The specification of an MF is subjective, which means that the MFs for the same concept (e.g., “sensible number of children in a family”) when specified by different persons may vary considerably. This subjectivity comes from individual differences in perceiving or expressing abstract concepts and has little to do with randomness. Therefore, the
subjectivity
and
nonrandomness
of fuzzy sets is the primary difference between the study of fuzzy sets and the probability theory, which deals with the objective treatment of random phenomena.
There are several parameters and characteristics of MF that are used very often in some fuzzy-set operations and fuzzy-set inference systems. We will define only some of them that are, in our opinion, the most important:
1.
Support
. The
support
of a fuzzy set A is the set of all points x in the universe of discourse X such that μ
A
(x) > 0:
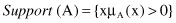
2.
Core
. The
core
of a fuzzy set A is the set of all points x in X such that μ
A
(x) = 1:

3.
Normalization
. A fuzzy set A is
normal
if its core is nonempty. In other words, we can always find a point x ∈ X such that μ
A
(x) = 1.
4.
Cardinality
. Given a fuzzy set A in a finite universe X, its cardinality, denoted by Card(A), is defined as
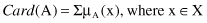
Often,
Card
(X) is referred to as the scalar cardinality or the count of A. For example, the fuzzy set A = 0.1/1 + 0.3/2 + 0.6/3 + 1.0/4 + 0.4/5 in universe X = {1, 2, 3, 4, 5, 6} has a cardinality
Card
(A) = 2.4.
5.
α-cut.
The
α-cut
or
α-level set
of a fuzzy set A is a crisp set defined by
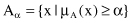
6.
Fuzzy number
. Fuzzy numbers are a special type of fuzzy sets restricting the possible types of MFs:
(a)
The MF must be normalized (i.e., the core is nonempty) and singular. This results in precisely one point, which lies inside the core, modeling the typical value of the fuzzy number. This point is called the modal value.
(b)
The MF has to monotonically increase the left of the core and monotonically decrease on the right. This ensures that only one peak and, therefore, only one typical value exists. The spread of the support (i.e., the nonzero area of the fuzzy set) describes the degree of imprecision expressed by the fuzzy number.