Data Mining (127 page)
Authors: Mehmed Kantardzic
subject to x ∈ X and y = f(x). Actually, in the expression above, the min operator is just a choice within a family of operators called triangular norms.
More specifically, suppose that f is a function from X to Y where X and Y are discrete universes of discourse, and A is a fuzzy set on X defined as
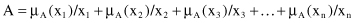
then the extension principle states that the image of fuzzy set A under the mapping f can be expressed as a fuzzy set B:

where y
i
= f(x
i
), i = 1, … , n. In other words, the fuzzy set B can be defined through the mapped values x
i
using the function f.
Let us analyze the extension principle using one example. Suppose that X = {1, 2, 3, 4} and Y = {1, 2, 3, 4, 5, 6} are two universes of discourse, and the function for transformation is y = x + 2. For a given fuzzy set A = 0.1/1 + 0.2/2 + 0.7/3 + 1.0/4 in X, it is necessary to find a corresponding fuzzy set B(y) in Y using the extension principle through function B = f(A). In this case, the process of computation is straightforward and a final, transformed fuzzy set is B = 0.1/3 + 0.2/4 + 0.7/5 + 1.0/6.
Another problem will show that the computational process is not always a one-step process. Suppose that A is given as

and the function f is

Upon applying the extension principle, we have
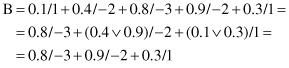
where ∨ represents the max function. For a fuzzy set with a continuous universe of discourse X, an analogous procedure applies.
Besides being useful in the application of the extension principle, some of the unary and binary fuzzy relations are also very important in a fuzzy-reasoning process. Binary fuzzy relations are fuzzy sets in X × Y that map each element in X × Y to a membership grade between 0 and 1. Let X and Y be two universes of discourse. Then
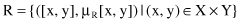
is a binary fuzzy relation in X × Y. Note that μ
R
(x, y) is in fact a two-dimensional (2-D) MF. For example, let X = Y = R
+
(the positive real axis); the fuzzy relation is given as R = “y is much greater than x.” The MF of the fuzzy relation can be subjectively defined as

If X and Y are a finite set of discrete values such as X {3, 4, 5} and Y = {3, 4, 5, 6, 7}, then it is convenient to express the fuzzy relation R as a relation matrix:

where the element at row i and column j is equal to the membership grade between the i
th
element of X and the j
th
element of Y.
Common examples of binary fuzzy relations are as follows:
1.
x is close to y (x and y are numbers).
2.
x depends on y (x and y are categorical data).
3.
x and y look alike.
4.
If x is large, then y is small.
Fuzzy relations in different product spaces can be combined through a composition operation. Different composition operations have been suggested for fuzzy relations; the best known is the max–min composition proposed by Zadeh. Let R
1
and R
2
be two fuzzy relations defined on X × Y and Y × Z, respectively. The max–min composition of R
1
and R
2
is a fuzzy set defined by

or equivalently,
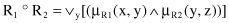
with the understanding that ∨ and ∧ represent max and min, respectively.
When R1 and R2 are expressed as relation matrices, the calculation of R
1
° R
2
is similar to the matrix-multiplication process, except that × and + operations are replaced by ∨ and ∧, respectively.
The following example demonstrates how to apply the max–min composition on two relations and how to interpret the resulting fuzzy relation R
1
° R
2
. Let R
1
= “x is relevant to y” and R
2
= “y is relevant to z” be two fuzzy relations defined on X × Y and Y × Z, where X = {1, 2, 3}, Y = {α, β, γ, δ}, and Z = {a, b}. Assume that R
1
and R
2
can be expressed as the following relation matrices of μ values:
