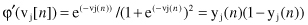Data Mining (62 page)
Authors: Mehmed Kantardzic
and
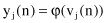
where m is the number of inputs for j
th
neuron. Also, we use the symbol v as a shorthand notation of the previously defined variable
net
. The backpropagation algorithm applies a correction Δw
ji
(
n
) to the synaptic weight w
ji
(
n
), which is proportional to the partial derivative δE(
n
)/δw
ji
(
n
). Using the chain rule for derivation, this partial derivative can be expressed as
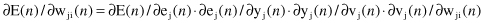
The partial derivative δE(
n
)/δwji(
n
) represents a sensitive factor, determining the direction of search in weight space. Knowing that the next relations
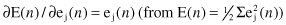
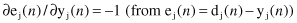
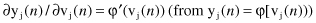

are valid, we can express the partial derivative ∂E(
n
)/∂w
ji
(
n
) in the form
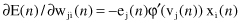
The correction Δw
ji
(
n
) applied to w
ji
(
n
) is defined by the delta rule

where η is the learning-rate parameter of the backpropagation algorithm. The use of the minus sign accounts for gradient descent in weight space, that is, a direction for weight change that reduces the value E(
n
). Asking for φ′(v
j
[
n
]) in the learning process is the best explanation for why we prefer continuous functions such as log-sigmoid and hyperbolic as a standard-activation function at the node level. Using the notation δ
j
(
n
) = e
j
(
n
)· , where δ
, where δ
j
(
n
) is the
local gradient
, the final equation for w
ji
(
n
) corrections is
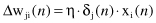
The local gradient δ
j
(
n
) points to the required changes in synaptic weights. According to its definition, the local gradient δ
j
(
n
) for output neuron j is equal to the product of the corresponding error signal e
j
(
n
) for that neuron and the derivative φ′(v
j
[
n
]) of the associated activation function.
Derivative φ′(v
j
[
n
]) can be easily computed for a standard activation function, where differentiation is the only requirement for the function. If the activation function is sigmoid, it means that in the form
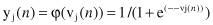
the first derivative is