Data Mining (63 page)
Authors: Mehmed Kantardzic
and a final weight correction is
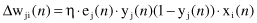
The final correction Δw
ji
(
n
) is proportional to the learning rate η, the error value at this node is e
j
(
n
), and the corresponding input and output values are x
i
(
n
) and y
j
(
n
). Therefore, the process of computation for a given sample
n
is relatively simple and straightforward.
If the activation function is a hyperbolic tangent, a similar computation will give the final value for the first derivative φ′(v
j
[
n
]):
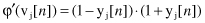
and
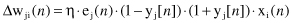
Again, the practical computation of Δw
ji
(
n
) is very simple because the local-gradient derivatives depend only on the output value of the node y
j
(
n
).
In general, we may identify two different cases of computation for Δw
ji
(
n
), depending on where in the network neuron j is located. In the first case, neuron j is an output node. This case is simple to handle because each output node of the network is supplied with a desired response, making it a straightforward matter to calculate the associated error signal. All previously developed relations are valid for output nodes without any modifications.
In the second case, neuron j is a hidden node. Even though hidden neurons are not directly accessible, they share responsibility for any error made at the output of the network. We may redefine the local gradient δ
j
(
n
) for a hidden neuron j as the product of the associated derivative φ′(v
j
[
n
]) and the weighted sum of the local gradients computed for the neurons in the next layer (hidden or output) that are connected to neuron j
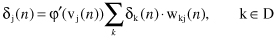
where D denotes the set of all nodes on the next layer that are connected to the node j. Going backward, all δ
k
(
n
) for the nodes in the next layer are known before computation of the local gradient δ
j
(
n
) for a given node on a layer closer to the inputs.
Let us analyze once more the application of the backpropagation-learning algorithm with two distinct passes of computation that are distinguished for each training example. In the first pass, which is referred to as the forward pass, the function signals of the network are computed on a neuron-by-neuron basis, starting with the nodes on first hidden layer (the input layer is without computational nodes), then the second, and so on, until the computation is finished with final output layer of nodes. In this pass, based on given input values of each learning sample, a network computes the corresponding output. Synaptic weights remain unaltered during this pass.
The second, backward pass, on the other hand, starts at the output layer, passing the error signal (the difference between the computed and the desired output value) leftward through the network, layer by layer, and recursively computing the local gradients δ for each neuron. This recursive process permits the synaptic weights of the network to undergo changes in accordance with the delta rule. For the neuron located at the output layer, δ is equal to the error signal of that neuron multiplied by the first derivative of its nonlinearity represented in the activation function. Based on local gradients δ, it is straightforward to compute Δw for each connection to the output nodes. Given the δ values for all neurons in the output layer, we use them in the previous layer before (usually the hidden layer) to compute modified local gradients for the nodes that are not the final, and again to correct Δw for input connections for this layer. The backward procedure is repeated until all layers are covered and all weight factors in the network are modified. Then, the backpropagation algorithm continues with a new training sample. When there are no more training samples, the first iteration of the learning process finishes. With the same samples, it is possible to go through a second, third, and sometimes hundreds of iterations until error energy E
av
for the given iteration is small enough to stop the algorithm.
The backpropagation algorithm provides an “approximation” to the trajectory in weight space computed by the method of steepest descent. The smaller we make the learning rate parameter η, the smaller the changes to the synaptic weights in the network will be from one iteration to the next and the smoother will be the trajectory in weight space. This improvement, however, is attained at the cost of a slower rate of learning. If, on the other hand, we make η too large in order to speed up the learning process, the resulting large changes in the synaptic weights can cause the network to become unstable, and the solution will become oscillatory about a minimal point never reaching it.
A simple method of increasing the rate of learning yet avoiding the danger of instability is to modify the delta rule by including a
momentum term
:
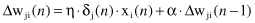
where α is usually a positive number called momentum constant and Δw
ji
(
n
− 1) is the correction of the weight factor for a previous (
n
− 1)
th
sample. α, in practice, is usually set to the value between 0.1 and 1. The addition of the momentum term smoothes the weight updating and tends to resist erratic weight changes because of gradient noise or high-spatial frequencies in the error surface. However, the use of momentum terms does not always seem to speed up training; it is more or less application-dependent. The momentum factor represents a method of averaging; rather than averaging derivatives, momentum averages the weight changes themselves. The idea behind momentum is apparent from its name: including some kind of inertia in weight corrections. The inclusion of the momentum term in the backpropagation algorithm has a stabilizing effect in cases where corrections in weight factors have a high oscillation and sign changes. The momentum term may also have the benefit of preventing the learning process from terminating in a shallow local minimum on the error surface.
Reflecting practical approaches to the problem of determining the optimal architecture of the network for a given task, the question about the values for three parameters, the number of hidden nodes (including the number of hidden layers), learning rate η, and momentum rate α, becomes very important. Usually the optimal architecture is determined experimentally, but some practical guidelines exist. If several networks with different numbers of hidden nodes give close results with respect to error criteria after the training, then the best network architecture is the one with smallest number of hidden nodes. Practically, that means starting the training process with networks that have a small number of hidden nodes, increasing this number, and then analyzing the resulting error in each case. If the error does not improve with the increasing number of hidden nodes, the latest analyzed network configuration can be selected as optimal. Optimal learning and momentum constants are also determined experimentally, but experience shows that the solution should be found with η about 0.1 and α about 0.5.
When the ANN is first set up, the initial weight factors must be given. The goal in choosing these values is to begin the learning process as fast as possible. The appropriate method is to take the initial weights as very small evenly distributed random numbers. That will cause the output values to be in mid-range regardless of the values of its inputs, and the learning process will converge much faster with every new iteration.
In backpropagation learning, we typically use the algorithm to compute the synaptic weights by using as many training samples as possible. The hope is that the neural network so designed will generalize the best. A network is said to generalize well when the input–output mapping computed by the network is correct for test data never used earlier in creating or training the network. In the MLP, if the number of hidden units is less that the number of inputs, the first layer performs a dimensionality reduction. Each hidden unit may be interpreted as defining a template. By analyzing these templates we can extract knowledge from a trained ANN. In this interpretation weights are defining relative importance in the templates. But the largest number of training samples and the largest number of learning iterations using these samples do not necessarily lead to the best generalization. Additional problems occur during the learning process, and they are briefly described through the following analysis.
The learning process using an ANN may be viewed as a curve-fitting problem. Such a viewpoint then permits us to look on generalization not as a theoretical property of neural networks but as the effect of a good, nonlinear interpolation of the input data. An ANN that is designed to generalize well will produce a correct input–output mapping, even when the input is slightly different from the samples used to train the network, as illustrated in Figure
7.11
a. When, however, an ANN learns from too many input–output samples, the network may end up memorizing the training data. Such a phenomenon is referred to as
overfitting
or
overtraining
. This problem has already been described in Chapter 4. When the network is overtrained, it loses the ability to generalize between similar patterns. A smoothness of input–output mapping, on the other hand, is closely related to the generalization abilities of an ANN. The essence is to select, based on training data, the simplest function for generalization, that means the smoothest function that approximates the mapping for a given error criterion. Smoothness is natural in many applications, depending on the scale of the phenomenon being studied. It is therefore important to seek a smooth nonlinear mapping, so that the network is able to classify novel patterns correctly with respect to the training patterns. In Figure
7.11
a,b, a fitting curve with a good generalization and an overfitted curve are represented for the same set of training data.