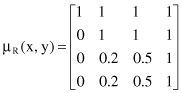Data Mining (128 page)
Authors: Mehmed Kantardzic

Fuzzy relation R
1
° R
2
can be interpreted as a derived relation “x is relevant to z” based on relations R
1
and R
2
. We will make a detailed max–min composition only for one element in a resulting fuzzy relation: (x, z) = (2, a).

Analogously, we can compute the other elements, and the final fuzzy matrix R
1
° R
2
will be

14.4 FUZZY LOGIC AND FUZZY INFERENCE SYSTEMS
Fuzzy logic enables us to handle uncertainty in a very intuitive and natural manner. In addition to making it possible to formalize imprecise data, it also enables us to do arithmetic and Boolean operations using fuzzy sets. Finally, it describes the inference systems based on fuzzy rules. Fuzzy rules and fuzzy-reasoning processes, which are the most important modeling tools based on the fuzzy-set theory, are the backbone of any fuzzy inference system. Typically, a fuzzy rule has the general format of a conditional proposition. A
fuzzy If-then rule
, also known as
fuzzy implication,
assumes the form
If x is A, then y is B
where A and B are linguistic values defined by fuzzy sets on the universes of discourse X and Y, respectively. Often, “x is A” is called the antecedent or premise, while “y is B” is called the consequence or conclusion. Examples of fuzzy if-then rules are widespread in our daily linguistic expressions, such as the following:
1.
If pressure is high, then volume is small.
2.
If the road is slippery, then driving is dangerous.
3.
If a tomato is red, then it is ripe.
4.
If the speed is high, then apply the brake a little.
Before we can employ fuzzy if-then rules to model and analyze a fuzzy reasoning-process, we have to formalize the meaning of the expression “if x is A then y is B,” sometimes abbreviated in a formal presentation as A → B. In essence, the expression describes a relation between two variables x and y; this suggests that a fuzzy if-then rule be defined as a binary fuzzy relation R on the product space X × Y. R can be viewed as a fuzzy set with a 2-D MF:

If we interpret A → B as A
entails
B, still it can be formalized in several different ways. One formula that could be applied based on a standard logical interpretation, is
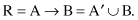
Note that this is only one of several possible interpretations for fuzzy implication. The accepted meaning of A → B represents the basis for an explanation of the fuzzy-reasoning process using if-then fuzzy rules.
Fuzzy reasoning, also known as approximate reasoning, is an inference procedure that derives its conclusions from a set of fuzzy rules and known facts (they also can be fuzzy sets). The basic rule of inference in a traditional two-valued logic is
modus ponens
, according to which we can infer the truth of a proposition B from the truth of A and the implication A → B. However, in much of human reasoning,
modus ponens
is employed in an approximate manner. For example, if we have the rule “if the tomato is red, then it is ripe” and we know that “the tomato is more or less red,” then we may infer that “the tomato is more or less ripe.” This type of approximate reasoning can be formalized as
Fact: x is A′
Rule: If x is A then y is B
Conclusion: y is B′
where A′ is close to A and B′ is close to B. When A, A′, B, and B′ are fuzzy sets of an approximate universe, the foregoing inference procedure is called approximate reasoning or fuzzy reasoning; it is also called
generalized modus ponens
, since it has
modus ponens
as a special case.
Using the composition rule of inference, we can formulate the inference procedure of fuzzy reasoning. Let A, A′, and B be fuzzy sets on X, X, and Y domains, respectively. Assume that the fuzzy implication A → B is expressed as a fuzzy relation R on X × Y. Then the fuzzy set B′ induced by A′ and A → B is defined by
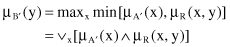
Some typical characteristics of the fuzzy-reasoning process and some conclusions useful for this type of reasoning are
1.
∀A, ∀ A′ → B′ ⊇ B ( \or μ
B′
(y) ≥ μ
B
(y))
2.
If A′ ⊆ A (or μ
A
(x) ≥ μ
A′
(x)) → B′ = B
Let us analyze the computational steps of a fuzzy-reasoning process for one simple example. Given the fact A′ = “x is above average height” and the fuzzy rule “if x is high, then his/her weight is also high,” we can formalize this as a fuzzy implication A → B. We can use a discrete representation of the initially given fuzzy sets A, A′, and B (based on subjective heuristics):

μ
R
(x, y) can be computed in several different ways, such as
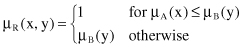
or as the Lukasiewicz norm:
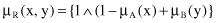
Both definitions lead to a very different interpretation of fuzzy implication. Applying the first relation for μ
R
(x, y) on the numeric representation for our sets A and B, the 2-D MF will be