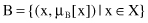Data Mining (122 page)

11. Search the Web to find the basic characteristics of publicly available or commercial software tools that are based on GAs. Document the results of your search.

13.9 REFERENCES FOR FURTHER STUDY

Fogel, D. B., ed.,
Evolutionary Computation
, IEEE Press, New York, 1998.

The book provides a collection of 30 landmark papers, and it spans the entire history of evolutionary computation—from today’s research back to its very origins more than 40 years ago.

Goldenberg, D. E.,
Genetic Algorithms in Search, Optimization and Machine Learning
, Addison Wesley, Reading, MA, 1989.

This book represents one of the first comprehensive texts on GAs. It introduces in a very systematic way most of the techniques that are, with small modifications and improvements, part of today’s approximate-optimization solutions.

Hruschka, E., R. Campello, A. Freitas, A. Carvalho, A Survey of Evolutionary Algorithms for Clustering,
IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews
, Vol. 39, No. 2, 2009, pp. 133–155.

This paper presents a survey of evolutionary algorithms designed for clustering tasks. It tries to reflect the profile of this area by focusing more on those subjects that have been given more importance in the literature. In this context, most of the paper is devoted to partitional algorithms that look for hard clustering of data, although overlapping (i.e., soft and fuzzy) approaches are also covered in the paper. The paper ends by addressing some important issues and open questions that can be the subjects of future research.

Michalewicz, Z.,
Genetic Algorithms
+
Data Structures
=
Evolution Programs
, Springer, Berlin, Germany, 1999.

This textbook explains the field of GAs in simple terms, and discusses the efficiency of its methods in many interesting test cases. The importance of these techniques is their applicability to many hard-optimization problems specified with large amounts of discrete data, such as the TSP, scheduling, partitioning, and control.

Chapter Objectives

• Explain the concept of fuzzy sets with formal interpretation in continuous and discrete domains.
  
• Analyze the characteristics of fuzzy sets and fuzzy-set operations.
  
• Describe the extension principle as a basic mechanism for fuzzy inferences.
  
• Discuss the importance of linguistic imprecision and computing with them in decision-making processes.
  
• Construct methods for multifactorial evaluation and extraction of a fuzzy rule-based model from large, numeric data sets.
  
• Understand why fuzzy computing and fuzzy systems are an important part of data-mining technology.
  

In the previous chapters, a number of different methodologies for the analysis of large data sets have been discussed. Most of the approaches presented, however, assume that the data are precise, that is, they assume that we deal with exact measurements for further analysis. Historically, as reflected in classical mathematics, we commonly seek a precise and crisp description of things or events. This precision is accomplished by expressing phenomena in numeric or categorical values. But in most, if not all, real-world scenarios, we will never have totally precise values. There is always going to be a degree of uncertainty. However, classical mathematics can encounter substantial difficulties because of this fuzziness. In many real-world situations, we may say that fuzziness is reality, whereas crispness or precision is simplification and idealization. The polarity between fuzziness and precision is quite a striking contradiction in the development of modern information-processing systems. One effective means of resolving the contradiction is the fuzzy-set theory, a bridge between high precision and the high complexity of fuzziness.

14.1 FUZZY SETS

Fuzzy concepts derive from fuzzy phenomena that commonly occur in the real world. For example, rain is a common natural phenomenon that is difficult to describe precisely since it can rain with varying intensity, anywhere from a light shower to a torrential downpour. Since the word rain does not adequately or precisely describe the wide variations in the amount and intensity of any rain event, “rain” is considered a fuzzy phenomenon.

Often, the concepts formed in the human brain for perceiving, recognizing, and categorizing natural phenomena are also fuzzy. The boundaries of these concepts are vague. Therefore, the judging and reasoning that emerges from them are also fuzzy. For instance, “rain” might be classified as “light rain,” “moderate rain,” and “heavy rain” in order to describe the degree of raining. Unfortunately, it is difficult to say when the rain is light, moderate, or heavy, because the boundaries are undefined. The concepts of “light,” “moderate,” and “heavy” are prime examples of fuzzy concepts themselves. To explain the principles of fuzzy sets, we will start with the basics in classical-set theory.

The notion of a set occurs frequently as we tend to organize, summarize, and generalize knowledge about objects. We can even speculate that the fundamental nature of any human being is to organize, arrange, and systematically classify information about the diversity of any environment. The encapsulation of objects into a collection whose members all share some general features naturally implies the notion of a set. Sets are used often and almost unconsciously; we talk about a set of even numbers, positive temperatures, personal computers, fruits, and the like. For example, a classical set A of real numbers greater than 6 is a set with a crisp boundary, and it can be expressed as

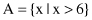
where there is a clear, unambiguous boundary 6 such that if x is greater than this number, then x belongs to the set A; otherwise, x does not belong to the set. Although classical sets have suitable applications and have proven to be an important tool for mathematics and computer science, they do not reflect the nature of human concepts and thoughts, which tend to be abstract and imprecise. As an illustration, mathematically we can express a set of tall persons as a collection of persons whose height is more than 6 ft; this is the set denoted by the previous equation, if we let A = “tall person” and x = “height.” Yet, this is an unnatural and inadequate way of representing our usual concept of “tall person.” The dichotomous nature of the classical set would classify a person 6.001 ft tall as a tall person, but not a person 5.999 ft tall. This distinction is intuitively unreasonable. The flaw comes from the sharp transition between inclusions and exclusions in a set.

In contrast to a classical set, a fuzzy set, as the name implies, is a set without a crisp boundary, that is, the transition from “belongs to a set” to “does not belong to a set” is gradual, and this smooth transition is characterized by membership functions (MFs) that give sets flexibility in modeling commonly used linguistic expressions such as “the water is hot” or “the temperature is high.” Let us introduce some basic definitions and their formalizations concerning fuzzy sets.

Let X be a space of objects and x be a generic element of X. A classical set A, A ⊆ X, is defined as a collection of elements or objects x ∈ X such that each x can either belong or not belong to set A. By defining a
characteristic function
for each element x in X, we can represent a classical set A by a set of ordered pairs (x, 0) or (x, 1), which indicates x ∉ A or x ∈ A, respectively.

Unlike the aforementioned conventional set, a fuzzy set expresses the degree to which an element belongs to a set. The characteristic function of a fuzzy set is allowed to have values between 0 and 1, which denotes the degree of membership of an element in a given set. If X is a collection of objects denoted generically by x, then a fuzzy set A in X is defined as a set of ordered pairs:

where μ
_A
(x) is called the membership function (MF) for the fuzzy set A. The MF maps each element of X to a membership grade (or membership value) between 0 and 1.

Obviously, the definition of a fuzzy set is a simple extension of the definition of a classical set in which the characteristic function is permitted to have any value between 0 and 1. If the value of the MF μ
_A
(x) is restricted to either 0 or 1, then A is reduced to a classic set and μ
_A
(x) is the characteristic function of A. For clarity, we shall also refer to classical sets as ordinary sets, crisp sets, non-fuzzy sets, or, simply, sets.

Usually X is referred to as the universe of discourse, or, simply, the universe, and it may consist of discrete (ordered or non-ordered) objects or continuous space. This can be clarified by the following examples. Let X = {San Francisco, Boston, Los Angeles} be the set of cities one may choose to live in. The fuzzy set C = “desirable city to live in” may be described as follows:

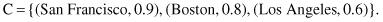
The universe of discourse X is discrete and it contains non-ordered objects: three big cities in the United States. As one can see, the membership grades listed above are quite subjective; anyone can come up with three different but legitimate values to reflect his or her preference.

In the next example, let X = {0, 1, 2, 3, 4, 5, 6} be a set of the number of children a family may choose to have. The fuzzy set A = “sensible number of children in a family” may be described as follows:

Or, in the notation that we will use through this chapter,

Here we have a discrete-order universe X; the MF for the fuzzy set A is shown in Figure
14.1
a. Again, the membership grades of this fuzzy set are obviously subjective measures.

Figure 14.1.
Discrete and continuous representation of membership functions for given fuzzy sets. (a) A = “sensible number of children”; (b) B = about 50 years old.

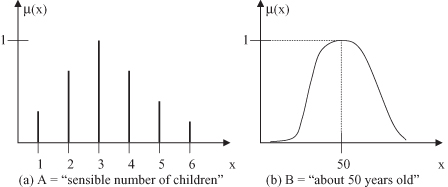
Finally, let X = R
⁺
be the set of possible ages for human beings. Then the fuzzy set B = “about 50 years old” may be expressed as