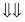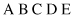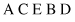Data Mining (117 page)

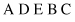
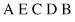
will produce new strings

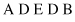
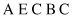
which are invalid solutions because they do not represent permutations of initial elements in the strings. To avoid this problem, a modified crossover operation is introduced that directly operates on permutations and still gives permutations. This is a
partially matched crossover
(PMC) operation. It can be used not only for the TSPs, but also for any other problems that involve permutations in a solution’s representation. We illustrate the effects of the PMC operation by an example. Assume that two solutions are given as permutations of the same symbols, and suppose that the PMC is a two-point operation. Selecting two strings and two random crossing points is the first step in the process of applying the PMC operation.

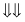
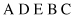
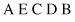
The substrings between crossing points are called matching sections. In our example, we have two elements in the matching sections: E B for the first string and C D for the second one. The crossover operation requires an exchange of the symbols E with C, denoted as an ordered pair (E, C), and B with D, represented as (B, D). The next step in the PMC operation is to permute each of these two-element permutations in each string. In other words, it is necessary to exchange the places for pairs (E, C) and (B, D) in both strings. The result of (E, C) changes in the first string is A D C B E, and after the second pair (B, D) has been changed, the final version of the first string is A B C D E. The second string after application of the same permutations will become A C E D B first, and then A C E B D finally. If we analyze the two strings obtained by PMC operation