Games and Mathematics (39 page)
Read Games and Mathematics Online
Authors: David Wells
Beauty and individual differences in perception
The general versus the specific and contingent
Beauty, form and understanding
Beauty is in the eye of the beholder.
Mathematicians cannot escape this everyday cliché. The vast landscape of modern mathematics guarantees that most mathematicians will only be at home in a small corner, and must lack the deeper understanding needed to make very delicate aesthetic judgements about regions of which they know little.
‘Which Is the Most Beautiful?’ was a questionnaire for readers of the
Mathematical Intelligencer
[Wells
1988
: 30–31] designed to test the plausible proposition that mathematicians no more agree on their judgements of beautiful mathematics than art lovers agree on favourite paintings or music lovers agree over Mozart and Beethoven. The items were chosen to be elementary, so that all respondents would be more-or-less familiar with all of them, (but see the comment on Ramanujan.)
Mathematical Intelligencer
[Wells
1988
: 30–31] designed to test the plausible proposition that mathematicians no more agree on their judgements of beautiful mathematics than art lovers agree on favourite paintings or music lovers agree over Mozart and Beethoven. The items were chosen to be elementary, so that all respondents would be more-or-less familiar with all of them, (but see the comment on Ramanujan.)
It worked well! The introduction quoted several classic comments such as John von Neumann's that, ‘I think it is correct to say that [the mathematician's]
criteria of selection, and also those of success, are mainly aesthetical,’ [von Neumann
1947
: 2053] and Poincaré's comment on this phenomenon: ‘It is true aesthetic feeling which all mathematicians recognise. The useful combinations are precisely the most beautiful’ [Poincaré 1914: 59]. In other words, the beauty of mathematics is not an add-on, it's not a bonus, and attention to beauty is not an option but an essential feature of mathematical creativity.
criteria of selection, and also those of success, are mainly aesthetical,’ [von Neumann
1947
: 2053] and Poincaré's comment on this phenomenon: ‘It is true aesthetic feeling which all mathematicians recognise. The useful combinations are precisely the most beautiful’ [Poincaré 1914: 59]. In other words, the beauty of mathematics is not an add-on, it's not a bonus, and attention to beauty is not an option but an essential feature of mathematical creativity.
The introduction also referred to theorems, proofs, concepts and strategies, because all these can be labelled
beautiful
. Readers were then given 24 theorems and asked to mark each of them from 0 to 10, the most beautiful getting the highest mark, and to add any comments they thought appropriate.
beautiful
. Readers were then given 24 theorems and asked to mark each of them from 0 to 10, the most beautiful getting the highest mark, and to add any comments they thought appropriate.
Responses from readers were predictable – they often agreed and often disagreed but – surprisingly, some of the disagreements were extreme. The Euler relationship, e
iπ
= −1 came top with an average of 7.7/10, but several readers thought it was too obvious and well-understood to be ranked highly.
iπ
= −1 came top with an average of 7.7/10, but several readers thought it was too obvious and well-understood to be ranked highly.
Euler won again with his polyhedron formula, V + F = E + 2, which tied second with ‘The number of primes is infinite’ on 7.5. The greatest surprise, however, was at the other end of the rankings. Equal last was a
partitions
identity from the great Ramanujan which J. E. Littlewood only 25 years previously had described as of ‘supreme beauty’:
p
(
n
) is the number of partitions of
n
:
partitions
identity from the great Ramanujan which J. E. Littlewood only 25 years previously had described as of ‘supreme beauty’:
p
(
n
) is the number of partitions of
n
:
Had aesthetic taste changed so much, so quickly? Or was Littlewood, perhaps, idiosyncratic even then? There is no doubt tastes do change – but that fits von Neumann's and Poincaré's claims: mathematicians ought to appreciate the ‘beauty’ that is most relevant to their own work, and partition theory is very special. I sympathise with Tito Tonietti who claimed that, ‘Beauty, even in mathematics, depends on historical and cultural contexts, and therefore tends to elude numerical interpretation.’
When they came to explain their choices there was somewhat more agreement. Several thought that you couldn't separate a theorem from its proof or its context and motivating ideas, but just about everyone agreed that simplicity and brevity were a plus though even here David Singmaster marked down Fermat's theorem that every prime of the form 4
n
+1 is uniquely the sum of two integer squares because it has no simple proof, while I am inclined to mark it up because it is that much more mysterious and, I suppose, deep. Are the most beautiful creations short lyrics or longer symphonies? Might apparent
depth merely be a sign that the theorem is not yet clearly understood? Simplicity contrasts also with surprise. 13+17=30 is incredibly simple but totally non-surprising, while Fermat's theorem is both simple and surprising.
n
+1 is uniquely the sum of two integer squares because it has no simple proof, while I am inclined to mark it up because it is that much more mysterious and, I suppose, deep. Are the most beautiful creations short lyrics or longer symphonies? Might apparent
depth merely be a sign that the theorem is not yet clearly understood? Simplicity contrasts also with surprise. 13+17=30 is incredibly simple but totally non-surprising, while Fermat's theorem is both simple and surprising.
Respondents did not highlight another difference which undoubtedly exists, as Freeman Dyson, a brilliant young mathematician who long ago became a world-class physicist, explains:
Unfashionable mathematics is mainly concerned with things of accidental beauty, special functions, particular number fields, exceptional algebras, sporadic finite groups. It is among these unorganized and undisciplined parts of mathematics that I would advise you to look for the next revolution in physics. They have a quality of strangeness, of unexpectedness. They do not fit easily into the smooth logical structures of Bourbaki
. Just for that reason we should cherish and cultivate them, remembering the words of Francis Bacon, ‘There is no beauty that hath not some strangeness in the proportion.’
Dyson could be proved right: there are currently believed to be deep connections between quantum mechanics, chaotic quantum systems, Riemann's zeta function, and random matrices.
Mathematicians have often found that progress lies through making sense of weird and strange phenomena – which are also surprising! – as we have already seen in the case of the complex ‘imaginary’ numbers.
Freeman Dyson continued: ‘The only thing these various discoveries had in common was a concrete, empirical, accidental quality, directly antithetical to the spirit of Bourbaki.’
Bourbaki was the pseudonym of a group of French mathematicians who promoted an extremely formal and abstract view of mathematics and ignored anything which didn't fit their pattern and their taste. Their perspective was very popular for a while and greatly influenced – for the worse – the school Modern Mathematics Movement of the 1960s but has since faded.
Paul Halmos highlights a similar contrast:
Stein's (harmonic analysis) and Shelah's (set theory) represent what seem to be two diametrically opposed psychological attitudes to mathematics…The contrast between the two can be described (inaccurately, but perhaps suggestively) by the words special and general…Stein talked about singular integrals…[Shelah] said, early on, ‘I love mathematics because I love generality,’ and he was off and running, classifying structures whose elements were structures of structures of structures.
It's a safe bet that Saharon Shelah, today a prolifically successful mathematician, professor at the Hebrew University of Jerusalem and at Rutgers University, is more sympathetic to Bourbaki.
On the other hand, even the most ‘exceptional’ objects such as the sporadic finite groups are known to have
some
connections with the rest of mathematics [Stillwell
1998
]. We might leave the last word, not for the first time, with David Hilbert: ‘He who seeks for methods without having a definite problem in mind seeks in the most part in vain.’
some
connections with the rest of mathematics [Stillwell
1998
]. We might leave the last word, not for the first time, with David Hilbert: ‘He who seeks for methods without having a definite problem in mind seeks in the most part in vain.’
Beauty, like some mythical Greek goddess, guides mathematicians to insight and understanding which, as it deepens, changes their perception of the form of the original problem and highlights the temporal nature of their original aesthetic judgement, but not to their loss, because with new perceptions come new insights and problems. Here is an example.
Euler's relationship e
iπ
= −1 is a special case of his formula,
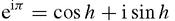whence,
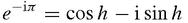and so
iπ
= −1 is a special case of his formula,
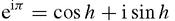
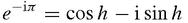
Hence cos
2
h
+ sin
2
h
= 1 the well-known formula which is equivalent to Pythagoras theorem – and which is extremely beautiful (to
most
mathematicians!) however you look at it. How do its attractions change, for better or for worse, if we write down the series for sin
x
and cos
x
,
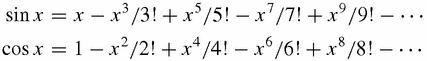then
start to
square them (you can never finish) and realise that the coefficient of every odd power of
x
in the product will be zero, and that the even powers in the product, beyond
x
0
=1, start,
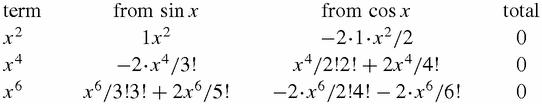
…and so on and so forth? This is a brute force calculation which is not in itself elegant. On the other hand, writing down the coefficients of
x
2
n
in the total you get a sequence of identities such as, from the
x
6
term,
plus similar identities for the higher coefficients, which are
not
obvious, so even this brutal calculation has suggested
something
– but in fact it suggests a possible conjecture too, that if a function which is represented by a power series is identically zero, then all its coefficients must be zero, and this happens to be a true theorem and a
deep
one.
2
h
+ sin
2
h
= 1 the well-known formula which is equivalent to Pythagoras theorem – and which is extremely beautiful (to
most
mathematicians!) however you look at it. How do its attractions change, for better or for worse, if we write down the series for sin
x
and cos
x
,
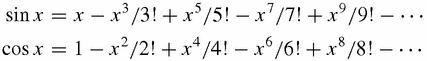
start to
square them (you can never finish) and realise that the coefficient of every odd power of
x
in the product will be zero, and that the even powers in the product, beyond
x
0
=1, start,
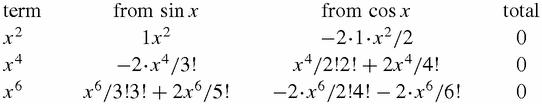
x
2
n
in the total you get a sequence of identities such as, from the
x
6
term,
not
obvious, so even this brutal calculation has suggested
something
– but in fact it suggests a possible conjecture too, that if a function which is represented by a power series is identically zero, then all its coefficients must be zero, and this happens to be a true theorem and a
deep
one.
Beauty depends on form but form also depends on beauty. The link is provided by the human brain's talent for spotting relationships which ensures that every step forward in understanding is accompanied by at least a pleasurable ‘kick’ and at best an overwhelming experience of euphoria. Different forms, however, display quite different properties and there is no guarantee that even the subtlest sense of beauty and sensitivity to patterns will necessarily allow us to resolve all the problems that we encounter.
Other books
The Penny Parker Megapack: 15 Complete Novels by Mildred Benson
The Clear-Out by Deborah Ellis
Happy Birthday or Whatever by Annie Choi
Giants (A Distant Eden Book 6) by Tackitt, Lloyd
The Girl Who Ran Off With Daddy by David Handler
License to Ensorcell by Kerr, Katharine
Aurora 07 - Last Scene Alive by Charlaine Harris
Open Road by M.J. O'Shea
Cop a Feel (Handcuffs and Happily Ever Afters) by Robyn Peterman
The Warrior Heir by Cinda Williams Chima