Games and Mathematics (35 page)
Read Games and Mathematics Online
Authors: David Wells
The skew quadrilateral
The neat
idea of ‘averaging’ two points offers an extra advantage. The mid-point of A and B is
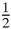 (A + B)
(A + B)
in any number of dimensions
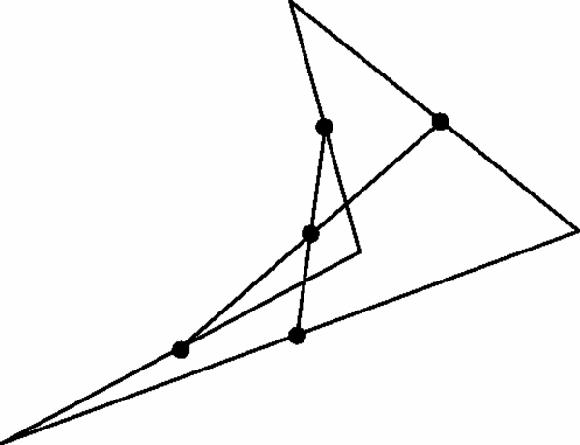
, so if we draw a skew quadrilateral (Figure
17.16
) – meaning that the four vertices and four edges do not all lie in one plane, then we can still conclude that the lines joining the mid-points of two pairs of sides will have a common mid-point, a fact which is certainly not immediately obvious.
idea of ‘averaging’ two points offers an extra advantage. The mid-point of A and B is
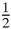 (A + B)
(A + B)in any number of dimensions
, so if we draw a skew quadrilateral (Figure
17.16
) – meaning that the four vertices and four edges do not all lie in one plane, then we can still conclude that the lines joining the mid-points of two pairs of sides will have a common mid-point, a fact which is certainly not immediately obvious.
Figure 17.16
Skew quadrilateral with two pairs of mid-points joined
Skew quadrilateral with two pairs of mid-points joined

Indeed it's not obvious that the mid-point lines even meet at all – most lines in three-dimensional space certainly do not. What is more, if we add two more edges to the skew quadrilateral
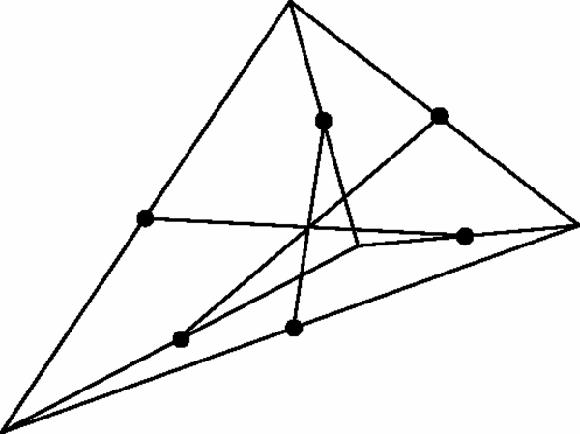
, to make a tetrahedron (Figure
17.17
) then we can conclude that all three lines joining the mid-points of the opposite edges of a tetrahedron, meet, and this is so in any number of dimensions.
, to make a tetrahedron (Figure
17.17
) then we can conclude that all three lines joining the mid-points of the opposite edges of a tetrahedron, meet, and this is so in any number of dimensions.
Figure 17.17
The same but all three pairs of mid-points joined
The same but all three pairs of mid-points joined

We can go further. We need not limit ourselves to merely averaging two points, we can also calculate
weighted
averages (Figure
17.18
).
weighted
averages (Figure
17.18
).
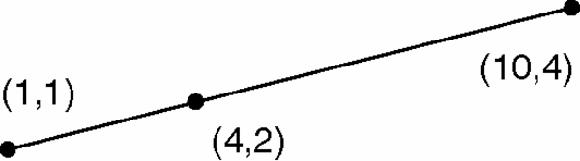
Figure 17.18
Line, with one of the one-third points marked X
Line, with one of the one-third points marked X

X is one third of the way from A to B, meaning it is twice as near to A as it is to B, so its coordinates will be the weighted average, (2A + B)/3 or (4,2). Suppose we take now take weighted averages of two pairs of the opposite sides of another skew quadrilateral, and join them (Figure
17.19
).
17.19
).
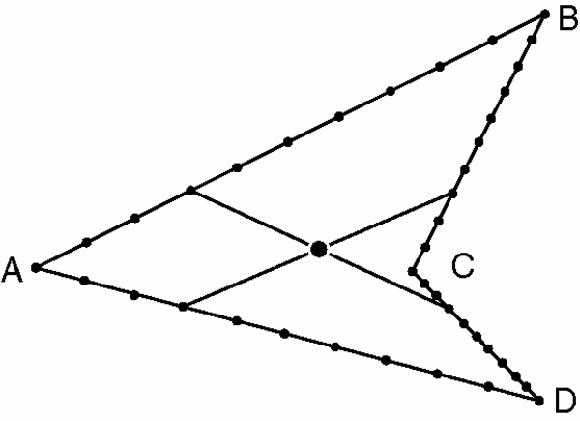
Figure 17.19
Skew quadrilateral with sides divided into 10 parts
Skew quadrilateral with sides divided into 10 parts

We have
joined two pairs of points: (7A+3B)/10 to (7C+3D)/10 and (7C+3B)/10 to (7A+3D)/10. These two chords meet in space at their shared mid-point, (7A + 3B + 7C + 3D)/20.
joined two pairs of points: (7A+3B)/10 to (7C+3D)/10 and (7C+3B)/10 to (7A+3D)/10. These two chords meet in space at their shared mid-point, (7A + 3B + 7C + 3D)/20.
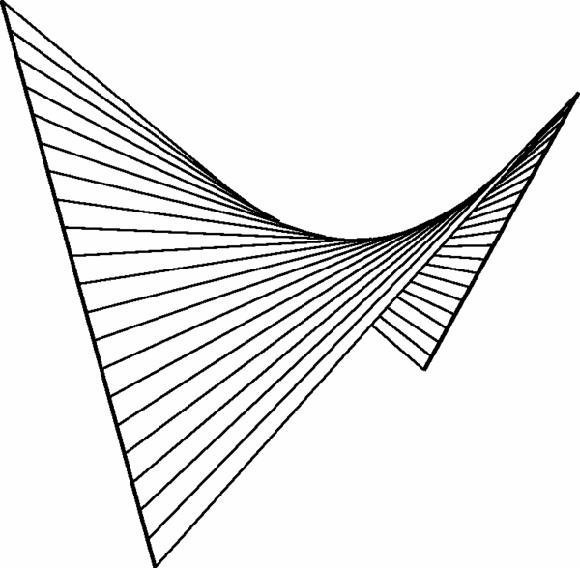
This may seem less than surprising, because there is a symmetry in our choice of the ends of the chords, but it so happens that two chords such as (2A+B)/3 to (2C+D)/3 and (3B+4C)/7 to (3D+4A)/7 will also meet in space, although they do not bisect each other. The fact is that ALL the chords in one set intersect ALL the chords in the other, forming a
ruled surface
which is a hyperbolic paraboloid (Figure
17.20
).
ruled surface
which is a hyperbolic paraboloid (Figure
17.20
).
Figure 17.20
Skew quadrilateral forms hyperbolic paraboloid
Skew quadrilateral forms hyperbolic paraboloid

This surface has several curious properties, one more curious than most: since a straight line is the shortest distance between two points and this surface consists of straight lines, you might think that it would be the
minimal surface
spanning the original skew quadrilateral, but it isn't, as Hermann Schwarz discovered in 1865. However, if the skew quadrilateral is chosen so that its edges are four diagonals of a cube, then the ratio of the areas of the surfaces is very close to 1, about 1.0012 [Dalpé
1998
: 6].
minimal surface
spanning the original skew quadrilateral, but it isn't, as Hermann Schwarz discovered in 1865. However, if the skew quadrilateral is chosen so that its edges are four diagonals of a cube, then the ratio of the areas of the surfaces is very close to 1, about 1.0012 [Dalpé
1998
: 6].
Pythagoras is a deep and beautiful theorem but these weighted averages without Pythagoras are pretty smooth too,
provided you only try to use them for appropriate problems
. That's the secret! Every problem has a structure behind it, at least that's what mathematicians assume. Find the correct structure and the problem turns out to be relatively easy, choose an inappropriate structure and it becomes difficult – and fail to find any structure and it is impossible, or can only be solved by checking.
provided you only try to use them for appropriate problems
. That's the secret! Every problem has a structure behind it, at least that's what mathematicians assume. Find the correct structure and the problem turns out to be relatively easy, choose an inappropriate structure and it becomes difficult – and fail to find any structure and it is impossible, or can only be solved by checking.
Much mathematical research consists of looking for the structures hidden behind problem situations. This is often an extremely difficult challenge because almost by definition you cannot afford to think only in familiar terms. You have to think new, deep thoughts, for which you need that old standby, imagination.
18
Hidden structure, common structure
The primes and the lucky numbers
Objects hidden behind a veil
Hidden structure, common structure
Gauss as a young teenager, maybe 14 or 15, (he recorded his experience many years later) conjectured on the basis of experimental calculation that the number of primes less than
n
is approximately
n
/log
n
. Since the primes are so weird anyway, we can hardly be surprised that this is an unusual formula but we may still wonder if it occurs elsewhere because any such analogy might help us to understand the prime numbers better.
n
is approximately
n
/log
n
. Since the primes are so weird anyway, we can hardly be surprised that this is an unusual formula but we may still wonder if it occurs elsewhere because any such analogy might help us to understand the prime numbers better.
Around about 1955 Stanislav Ulam (1909–1984) took an ingenious step in that direction by constructing a sequence by a process that is similar to the sieve of Erastosthenes, but different. The numbers that his technique generated, which he called the
lucky
numbers because they luckily escape being eliminated by the sieve, behave – surprise, surprise – much like the primes, in certain important respects.
lucky
numbers because they luckily escape being eliminated by the sieve, behave – surprise, surprise – much like the primes, in certain important respects.
We start with the sequence of positive integers and cross out all the even numbers, leaving the odd. The
second
integer remaining is 3, so cross out every third number to leave,
The
third
integer remaining is 7, so next cross out every seventh number, starting with 19. The fourth number left is 9, so cross out every ninth number, starting with 27, and so on. Hence the sequence of lucky numbers starts,
These are the lucky numbers and they share many properties with the primes. For a start, there are roughly similar numbers of each:
second
integer remaining is 3, so cross out every third number to leave,
1 | 3 | 7 | 9 | ||
1 | 3 | 15 | 19 | 21 | … |
third
integer remaining is 7, so next cross out every seventh number, starting with 19. The fourth number left is 9, so cross out every ninth number, starting with 27, and so on. Hence the sequence of lucky numbers starts,
1 | 3 | 7 | 9 | 13 | 15 | 21 | 25 | 31 | 33 | 37 | 43 | 49 |
51 | 63 | 67 | 69 | 73 | 75 | 79 | 87 | 93 | 99 | 105 | 111 | 115 |
127 | 129 | 133 | 135 | 141 | 151 | … |
The primes and luckies also become scarcer as they get larger, at about the same rate, so the number of luckies less than
n
is also approximately
n
/log
n
.
n
is also approximately
n
/log
n
.
There are also twin lucky numbers matching the twin primes: the first few twin luckies are: 1–3, 7–9, 13–15, 31–33, 49–51, 67–69, 73–75…and there are 33 twin luckies under 1000 compared to 35 twin primes.
The Lucky Goldbach Conjecture may well be true also. Computer checks by Walter Schneider up to 10
10
show that every even number to that limit is the sum of two luckies.
10
show that every even number to that limit is the sum of two luckies.
There are also roughly equal numbers of luckies of the forms 4
n
+ 1 and 4
n
+ 3, as there are for primes, but there are none of the form 3
n
+ 2, all of which are eliminated on the second stage of the Ulam sieve.
n
+ 1 and 4
n
+ 3, as there are for primes, but there are none of the form 3
n
+ 2, all of which are eliminated on the second stage of the Ulam sieve.
Are there more sequences, also created by sieves, that share these same properties? Mathematicians would like to know, because whatever primes and luckies have in common cannot be at the core of the unique nature of prime numbers.
Here are two quadratic functions,
x
2
+ 10 − 7
x
and
x
2
+ 10 − 6
x
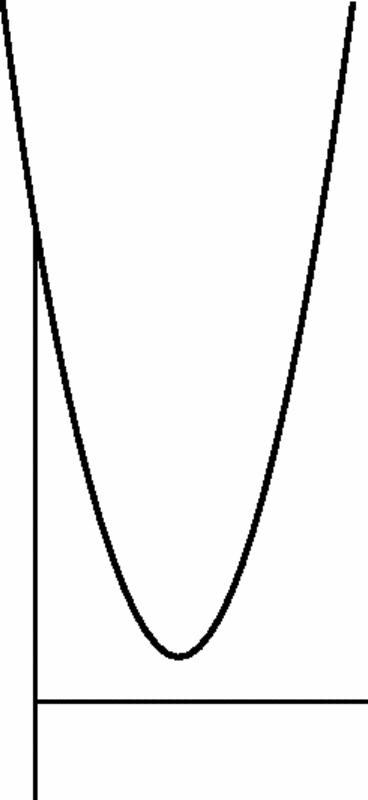
. The first has real zeros 2 and 5 (Figure
18.1
) but a graph of the second does not cross the
x
-axis (Figure
18.2
) and seems to have no geometrical roots.
x
2
+ 10 − 7
x
and
x
2
+ 10 − 6
x
. The first has real zeros 2 and 5 (Figure
18.1
) but a graph of the second does not cross the
x
-axis (Figure
18.2
) and seems to have no geometrical roots.
Figure 18.1
Parabola cutting both axes of graph
Parabola cutting both axes of graph

Figure 18.2
Parabola cutting one axis of graph
Parabola cutting one axis of graph

However, by algebra, the second equation has the two roots 3+
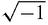 and 3 −
and 3 −
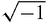 which involve ‘the square root of −1’. What should be done with them? Mathematicians who first came across these exotic objects were naturally intrigued, but also wary. They were labelled
which involve ‘the square root of −1’. What should be done with them? Mathematicians who first came across these exotic objects were naturally intrigued, but also wary. They were labelled
imaginary
in contrast to
real
and there was a temptation to regard them as absurd. What indeed could they possibly
mean
? The short answer is that the question itself is not quite right. A better question is, ‘What
ought
they to mean, what should we decide to
make them mean
in order to make maximum sense of the situation?’
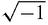 and 3 −
and 3 −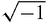 which involve ‘the square root of −1’. What should be done with them? Mathematicians who first came across these exotic objects were naturally intrigued, but also wary. They were labelled
which involve ‘the square root of −1’. What should be done with them? Mathematicians who first came across these exotic objects were naturally intrigued, but also wary. They were labelledimaginary
in contrast to
real
and there was a temptation to regard them as absurd. What indeed could they possibly
mean
? The short answer is that the question itself is not quite right. A better question is, ‘What
ought
they to mean, what should we decide to
make them mean
in order to make maximum sense of the situation?’
Looking at elementary algebra from our perspective, as a game, our first thought is to add
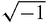 as just another piece in the game but to do so with confidence we need to know that this will never get us into trouble, that the square roots of negative numbers will always be consistent with the rest of the game. A first step is to ‘suck it and see’. Does basic algebra work with the addition of
as just another piece in the game but to do so with confidence we need to know that this will never get us into trouble, that the square roots of negative numbers will always be consistent with the rest of the game. A first step is to ‘suck it and see’. Does basic algebra work with the addition of
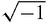 – not forgetting the roots of other negative numbers? Yes, seems to be the answer. We can add and subtract with no difficulty and multiplication and division and even powers seems to ‘work’ also. For example,
– not forgetting the roots of other negative numbers? Yes, seems to be the answer. We can add and subtract with no difficulty and multiplication and division and even powers seems to ‘work’ also. For example,
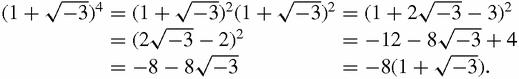
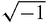 as just another piece in the game but to do so with confidence we need to know that this will never get us into trouble, that the square roots of negative numbers will always be consistent with the rest of the game. A first step is to ‘suck it and see’. Does basic algebra work with the addition of
as just another piece in the game but to do so with confidence we need to know that this will never get us into trouble, that the square roots of negative numbers will always be consistent with the rest of the game. A first step is to ‘suck it and see’. Does basic algebra work with the addition of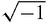 – not forgetting the roots of other negative numbers? Yes, seems to be the answer. We can add and subtract with no difficulty and multiplication and division and even powers seems to ‘work’ also. For example,
– not forgetting the roots of other negative numbers? Yes, seems to be the answer. We can add and subtract with no difficulty and multiplication and division and even powers seems to ‘work’ also. For example,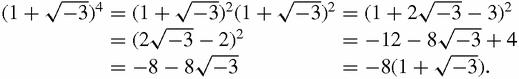
This suggests that (1+
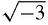 )
)
3
= −8 and so the three cube roots of −8, if it has
three
roots when complex numbers are included, should be −2, (1+
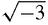 ) and one other. However, the product of the three roots should be 8, and so the third root should be, 8/2(1+
) and one other. However, the product of the three roots should be 8, and so the third root should be, 8/2(1+
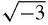 ) or
) or
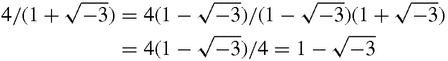 so it looks as if the roots of −8 are −2, and 1
so it looks as if the roots of −8 are −2, and 1
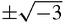 . Sure enough,
. Sure enough,
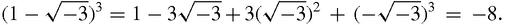 This kind of playing around with complex numbers seems never to lead to contradictions, which is encouraging, even convincing, but
This kind of playing around with complex numbers seems never to lead to contradictions, which is encouraging, even convincing, but
proves
nothing.
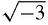 )
)3
= −8 and so the three cube roots of −8, if it has
three
roots when complex numbers are included, should be −2, (1+
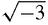 ) and one other. However, the product of the three roots should be 8, and so the third root should be, 8/2(1+
) and one other. However, the product of the three roots should be 8, and so the third root should be, 8/2(1+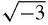 ) or
) or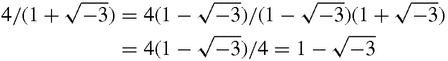 so it looks as if the roots of −8 are −2, and 1
so it looks as if the roots of −8 are −2, and 1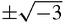 . Sure enough,
. Sure enough,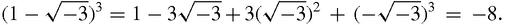
proves
nothing.
Other books
Oscar and Lucinda by Peter Carey
Beneath The Skin (A College Obsession Romance) by Daryl Banner
For Fallon by Soraya Naomi
Byrne's Dictionary of Irish Local History by Joseph Byrne
Fighting for Dear Life by David Gibbs
The Bachelor's Promise (Bachelor Auction) by Naima Simone
Warning Track by Meghan Quinn
Finn Finnegan by Darby Karchut
Pelquin's Comet by Ian Whates