Games and Mathematics (31 page)
Read Games and Mathematics Online
Authors: David Wells
Napoleon's theorem
The polygonal numbers



Napoleon's
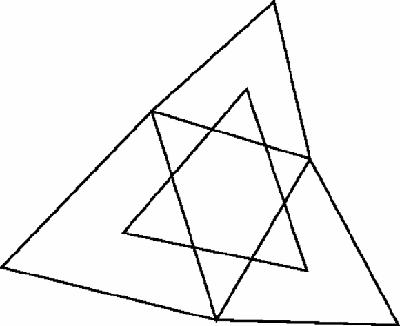
theorem, named after the French emperor who was also an amateur mathematician, says that if you construct equilateral triangles on the sides of any triangle, the centres form another equilateral triangle (Figure
16.4
).
theorem, named after the French emperor who was also an amateur mathematician, says that if you construct equilateral triangles on the sides of any triangle, the centres form another equilateral triangle (Figure
16.4
).
Figure 16.4
Napoleon figure
Napoleon figure

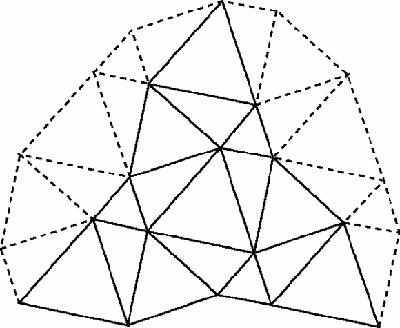
The same is true if the equilateral triangles are drawn on the opposite sides, facing inwards. The first case can be proved by continuing the figure to create the tessellation (Figure
16.5
a) which has rotational symmetry.
16.5
a) which has rotational symmetry.
Figure 16.5a
Napoleon tesselation – 1
Napoleon tesselation – 1

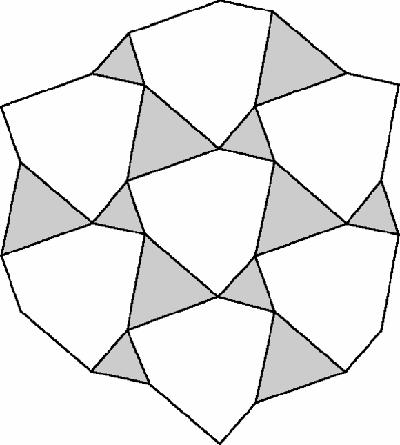
We can delete some of the lines and highlight some of the triangles to make the rotational symmetry even more obvious (Figure
16.5b
).
16.5b
).
Figure 16.5b
Napoleon tesselation – 2
Napoleon tesselation – 2

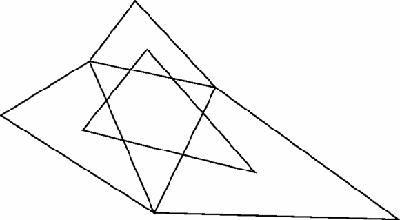
Napoleon's theorem
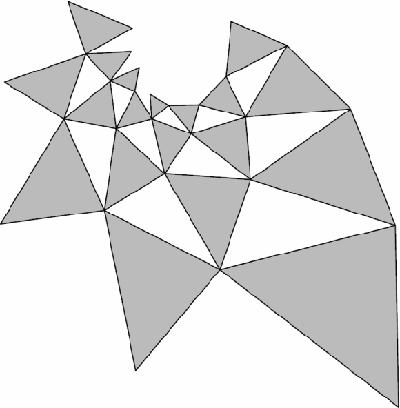
might seem just one more idiosyncratic, attractive and intriguing property from elementary Euclidean geometry. However, we can generalise it to show that this is not so. Draw the tessellation in Figure
16.6
– which if continued collapses into a limit point at the top of the figure – and we get a different perspective.
might seem just one more idiosyncratic, attractive and intriguing property from elementary Euclidean geometry. However, we can generalise it to show that this is not so. Draw the tessellation in Figure
16.6
– which if continued collapses into a limit point at the top of the figure – and we get a different perspective.
Figure 16.6
Napoleon spiral tesselation
Napoleon spiral tesselation

This tessellation ‘works’ with triangles of any two different shapes. Now look carefully (as always) at the bit of the tesselation shown in Figure
16.7
.
16.7
.
Figure 16.7
Napoleon with non-central points
Napoleon with non-central points

According to the tessellation, any three corresponding points in the three outer triangles will form a triangle of the same shape. Make them all equilateral and choose their centres and – ‘Hey presto!’ – Napoleon's theorem. This novel
perspective on Napoleon's theorem has many more consequences [Wells
1988
: Chapter
6
] [Wells
1995
: 178–184].
perspective on Napoleon's theorem has many more consequences [Wells
1988
: Chapter
6
] [Wells
1995
: 178–184].
What is
the sum of the counting numbers, from 1?
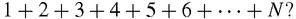 We can find the answer to this question from Figures
We can find the answer to this question from Figures
16.8
and
16.9
which illustrates the sum 1 to 7.
the sum of the counting numbers, from 1?
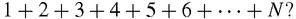
16.8
and
16.9
which illustrates the sum 1 to 7.
Figure 16.8
Divided rectangle to show 1 + 2 + 3 ⋯
Divided rectangle to show 1 + 2 + 3 ⋯

Figure 16.9
Divided rectangle – second version
Divided rectangle – second version

The rectangle in Figure
16.8
is 7 by 8 and has been dissected into two identical parts, each with an area of 1 + 2 + 3 + 4 + 5 + 6 + 7, so that total must be 1/2 of 7 × 8 = 28. For the sum 1 to 8 the slightly different arrangement in Figure
16.9
shows that the answer is now 1/2 of 8 × 9.
16.8
is 7 by 8 and has been dissected into two identical parts, each with an area of 1 + 2 + 3 + 4 + 5 + 6 + 7, so that total must be 1/2 of 7 × 8 = 28. For the sum 1 to 8 the slightly different arrangement in Figure
16.9
shows that the answer is now 1/2 of 8 × 9.
This idea can be applied to any sequence of the counting numbers from 1, so the answer to our question seems clearly to be
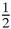 N
N
(
N
+1). The same idea proves-by-looking that the first
N
odd numbers sum to
N
2
, a square number (Figure
16.10
)
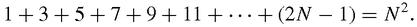
 N
N(
N
+1). The same idea proves-by-looking that the first
N
odd numbers sum to
N
2
, a square number (Figure
16.10
)
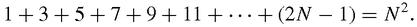
Figure 16.10
Square divided into gnomons
Square divided into gnomons

Other books
In the Image of Grace by Charlotte Ann Schlobohm
Witches: The Absolutely True Tale of Disaster in Salem by Rosalyn Schanzer
Undressed by Aster, Avery
The Alchemist's Key by Traci Harding
QuarterLifeFling by Clare Murray
Chore Whore by Heather H. Howard
Descent Into Madness by Catherine Woods-Field
The Diary of a Chambermaid by Octave Mirbeau
DIVA by Susan Fleet