Games and Mathematics (29 page)
Read Games and Mathematics Online
Authors: David Wells
In
Descartes's time, that idea had not been invented (or discovered), but he drew the same conclusion by a more complicated argument about a polygon, ending up by exclaiming that, ‘the same would happen with a polygon with one hundred thousand million sides, and consequently also with the circle.’ He was right. It would. He continued,
Descartes's time, that idea had not been invented (or discovered), but he drew the same conclusion by a more complicated argument about a polygon, ending up by exclaiming that, ‘the same would happen with a polygon with one hundred thousand million sides, and consequently also with the circle.’ He was right. It would. He continued,
By ‘more geometric’ Descartes meant that his other proof, which he never revealed, did not involve ideas of motion or mechanism. Descartes believed that ‘mechanical’ curves such as the cycloid
should be banished from ‘proper’ geometry, unlike Pascal who was happy to welcome them. Fortunately, Descartes did not let his prejudice stand in the way of his curiosity [Jesseph
2007
: 423].
should be banished from ‘proper’ geometry, unlike Pascal who was happy to welcome them. Fortunately, Descartes did not let his prejudice stand in the way of his curiosity [Jesseph
2007
: 423].
Whatever the explanation – if there is one – the success of mathematics in (hard) science has been a boon to both: scientists have been able to create very powerful theories, while mathematicians have been forced – or inspired – by scientific questions to develop their own theories.
The calculus could have been used merely to find areas under curves and gradients of tangents more efficiently, but no, it was used at once to solve difficult new problems such as the problem of the shape of a solid which offered least resistance to a flowing liquid, and the problem of the path of light through different media [
Chapter 15
], and of course in Newton's wonderful theory of universal gravitation. The mutual fertilisation continues to the present day.
Chapter 15
], and of course in Newton's wonderful theory of universal gravitation. The mutual fertilisation continues to the present day.
In contrast, the fate of mathematics without science is illustrated by traditional Japanese mathematics
,
wasan
. Japanese mathematics in the pre-feudal era was utilitarian but during the Edo period (1603–1867) it lost its practical character and became the hobby of leisured samurai, merchants and rich peasants who enjoyed
wasan
much as they enjoyed
haiku
or the tea ceremony as an art form unconnected to everyday life.
,
wasan
. Japanese mathematics in the pre-feudal era was utilitarian but during the Edo period (1603–1867) it lost its practical character and became the hobby of leisured samurai, merchants and rich peasants who enjoyed
wasan
much as they enjoyed
haiku
or the tea ceremony as an art form unconnected to everyday life.
The greatest
wasan
practitioner was Seki Kowa (c.1642–1708), a genius whose achievements included finding Horner's method for solving algebraic equations with numerical coefficients long before Horner, the concept of the discriminant of an equation, developing the Chinese idea of determinants ten years before Leibniz, and discovering the Bernoulli numbers, the Pappus–Guldin theorem and using negative and imaginary roots. Either Seki or his disciples also created the
enri
calculus through their study of arcs of circles, which they applied to curves and curved surfaces generally. However, this is where differences with the West appear:
wasan
practitioner was Seki Kowa (c.1642–1708), a genius whose achievements included finding Horner's method for solving algebraic equations with numerical coefficients long before Horner, the concept of the discriminant of an equation, developing the Chinese idea of determinants ten years before Leibniz, and discovering the Bernoulli numbers, the Pappus–Guldin theorem and using negative and imaginary roots. Either Seki or his disciples also created the
enri
calculus through their study of arcs of circles, which they applied to curves and curved surfaces generally. However, this is where differences with the West appear:
The
enri
calculus
, which developed from problems concerning the arc, an important topic in astronomy, coincided in its results with Western-style calculus. The course it followed…was completely different from that of Western mathematics, which began with problems in dynamics…There were greater limits to the problem development possible in
enri
. Ultimately the absence of kinematic and dynamic problems in Japan's scientific tradition handicapped and retarded
wasan
's approach to analysis and proved decisive in its race with the Western tradition.
The
wasan
mathematicians had their own aesthetic criteria:
wasan
mathematicians had their own aesthetic criteria:
The purer the mathematical character of a problem and the greater its detachment from practicality, the greater the enthusiasm with which it was received.[Nakayama 1975: 749]
In bibliographies,
wasan
was listed with flower arranging and the tea ceremony, social activities with a strong aesthetic component, influenced by Zen Buddhism [Ravina
1993
: 206]. The other side of this coin was that
wasan
practitioners looked down on the sciences:
wasan
was listed with flower arranging and the tea ceremony, social activities with a strong aesthetic component, influenced by Zen Buddhism [Ravina
1993
: 206]. The other side of this coin was that
wasan
practitioners looked down on the sciences:
The demise of
wasan
stemmed largely from its divorce from the natural sciences…The natural world was deemed unsuitable as a subject of mathematical study. Mathematics advanced no new theories of the physical world, developed no new mechanical laws, challenged no theological principles, and produced no machines. Tokugawa scientists on neighbouring fields, such as astronomy and surveying, considered
wasan
intriguing but essentially useless.
As a result,
wasan
degenerated:
wasan
degenerated:
As time passed, the problems became more intricate and mulifaceted…There was an emphasis on solving problems by some unusual means or in presenting problems for which it was not known whether a satisfactory solution existed.[Nakayama 1975: 750]
John von Neumann expected our mathematics to degenerate also if it strayed too far from applications:
As a mathematical discipline travels far from its empirical source…if it is…only indirectly inspired by ideas coming from ‘reality’…It becomes more and more purely aestheticizing, more and more
l'art pour l'art
…there is a grave danger…that the stream .. will separate into a multitude of insignificant branches, and that the discipline will become a disorganized mass of details and complexities.
The interpretation of ‘applications’ is a moot point. It does not have to be applications to the sciences, but could be to other branches of mathematics. The creativity devoted to Fermat's Last Theorem
seems not to have degenerated over several hundred years, while Fermat's contribution to optics
is also still alive as we shall see shortly. In all the many miniature worlds of mathematics, cross-fertilisation is endemic, and fortunately so, because it forces the mathematician to face up to new challenges and prevents the degeneration that might otherwise attack the mathematical ivory tower aesthete.
seems not to have degenerated over several hundred years, while Fermat's contribution to optics
is also still alive as we shall see shortly. In all the many miniature worlds of mathematics, cross-fertilisation is endemic, and fortunately so, because it forces the mathematician to face up to new challenges and prevents the degeneration that might otherwise attack the mathematical ivory tower aesthete.
15
Minimum paths: elegant simplicity
A familiar puzzle
Developing Heron's theorem
Minimum paths: elegant simplicity
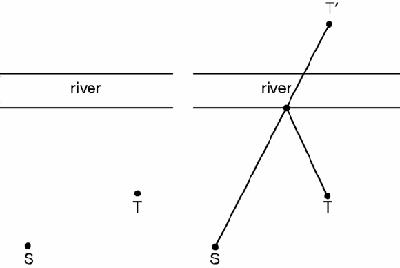
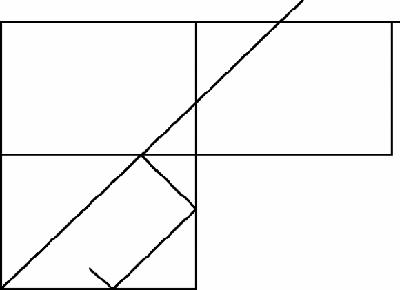
Mary, who is standing at S, wishes to walk to the river for a drink and then back to T, walking as short a distance as possible. To what point on the river bank should she walk?
The solution to this favourite puzzle is delightfully simple and elegant: reflect the point T in the river bank to Tʹ, and join STʹ. Mary walks on the line STʹ to the bank and then heads back to T (
Figure 15.1
).
Figure 15.1
).
Figure 15.1
To the river and back
To the river and back

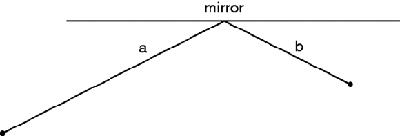
This problem, but expressed more seriously, was solved by Heron of Alexandria
(c.75 CE) in his
Catoptrica
. He asked how a ray of light is reflected off a mirror and answered that it takes the shortest path and that its angles of incidence and reflection are equal (
Figure 15.2
).
(c.75 CE) in his
Catoptrica
. He asked how a ray of light is reflected off a mirror and answered that it takes the shortest path and that its angles of incidence and reflection are equal (
Figure 15.2
).
Figure 15.2
Reflection of light in a mirror
Reflection of light in a mirror

It is a delightful feature that a problem about reflection of light is also solved by reflection.
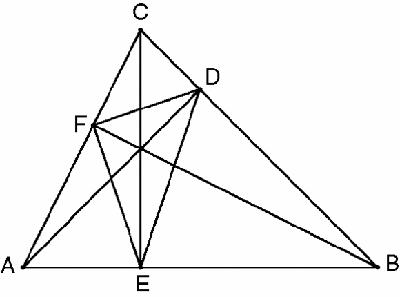
A
related problem is: to find the smallest triangle, measured by perimeter, that can be drawn in a given triangle (
Figure 15.3
). According to Heron's argument, the two lines FE and ED must meet the base AB at the same angle, because if they did not then we could adjust E slightly to reduce the length FE + ED. Similarly, FD and DE must strike BC at the same angles, and likewise EF and FD on AB. Therefore, if the solution exists, it is a triangle which is also the path of a ray of light being reflected endlessly round the inside the triangle. But does it exist? (Yes, it's the triangle formed by the base of the altitudes, so the triangle must be acute angled.)
related problem is: to find the smallest triangle, measured by perimeter, that can be drawn in a given triangle (
Figure 15.3
). According to Heron's argument, the two lines FE and ED must meet the base AB at the same angle, because if they did not then we could adjust E slightly to reduce the length FE + ED. Similarly, FD and DE must strike BC at the same angles, and likewise EF and FD on AB. Therefore, if the solution exists, it is a triangle which is also the path of a ray of light being reflected endlessly round the inside the triangle. But does it exist? (Yes, it's the triangle formed by the base of the altitudes, so the triangle must be acute angled.)
Figure 15.3
The shortest path in triangle
The shortest path in triangle

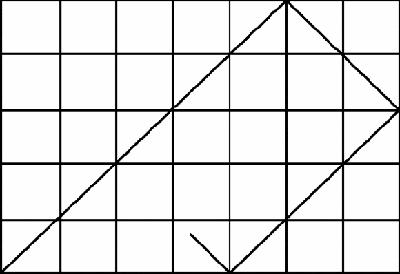
Other puzzles can also be solved by reflection: the next is a popular investigation for school pupils. The figure represents a billiard table. A ball shoots out of the corner at 45° to both sides, bounces round the table and ends up – where (
Figure 15.4
)? And how long does it take to get there?
Figure 15.4
)? And how long does it take to get there?
Figure 15.4
The billiard ball problem
The billiard ball problem

A
solution well-known among teachers starts by reflecting the table several times, so that the path of the ball as it is reflected off the cushes becomes a straight line: the start of this solution is illustrated in
Figure 15.5
. Jolly ingenious! But there is another solution, discovered by a 12-year-old pupil after hours of drawing and thinking, which uses an entirely different argument and which you might think was simpler and superior. It goes like this: to end up in any of the corners, the ball must have travelled the length of the table a whole number of times and so it will have travelled one of the distances in the first row:
solution well-known among teachers starts by reflecting the table several times, so that the path of the ball as it is reflected off the cushes becomes a straight line: the start of this solution is illustrated in
Figure 15.5
. Jolly ingenious! But there is another solution, discovered by a 12-year-old pupil after hours of drawing and thinking, which uses an entirely different argument and which you might think was simpler and superior. It goes like this: to end up in any of the corners, the ball must have travelled the length of the table a whole number of times and so it will have travelled one of the distances in the first row:
7 | 14 | 21 | 28 | 35 | 42 | 49 | 56… |
5 | 10 | 15 | 20 | 25 | 30 | 35 | 40… |
Figure 15.5
A solution by reflection
A solution by reflection

But it will also have travelled the width of the table a whole number of times, represented by the numbers in the second row. So the solution is found by comparing these lists to find a common number, which is 35.
This is impressive, but we can learn more. It travels the length of the table 5 times and so must end up at the righ-hand side of the table and it travels the width 7 times, so it ends up on the top edge. So it ends up in the top right corner.
We have not referred to 35 as
the lowest common multiple
of 5 and 7 because the pupil who discovered this method was too young to know the expression, though you could say that he half-discovered it in solving the puzzle.
the lowest common multiple
of 5 and 7 because the pupil who discovered this method was too young to know the expression, though you could say that he half-discovered it in solving the puzzle.
Billiards is an enjoyable game but the puzzle might seem to be mathematically trivial. Not at all! If we
generalise
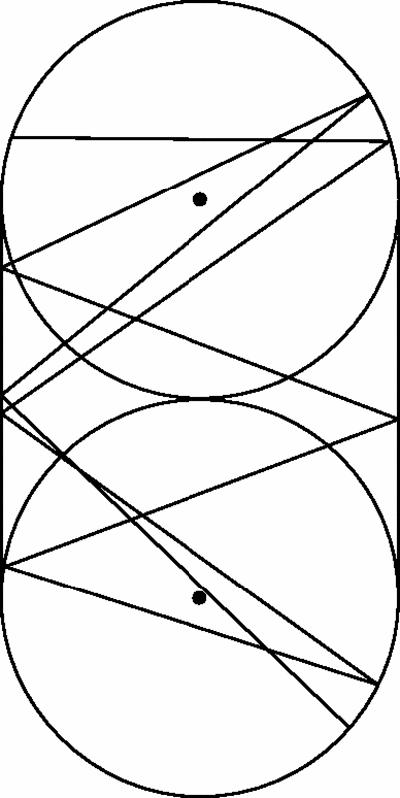
it and study other shapes of table we get physically interesting results. For example, in the circular table in
Figure 15.6
the path of a ball will cover, eventually, the whole of an annulus, but will never enter a central circle. (To be more precise, the path will eventually pass arbitrarily close to any point in the annulus.)
generalise
it and study other shapes of table we get physically interesting results. For example, in the circular table in
Figure 15.6
the path of a ball will cover, eventually, the whole of an annulus, but will never enter a central circle. (To be more precise, the path will eventually pass arbitrarily close to any point in the annulus.)
Figure 15.6
Billiards between two circles
Billiards between two circles

This motion is very regular when compared to
Figure 15.7
, made of semi-circles joined by straight lines and called the Bunimovich stadium
after the Russian mathematician who studied its properties. The path is quite irregular, in fact it's chaotic. Such models are used in mechanics.
Figure 15.7
, made of semi-circles joined by straight lines and called the Bunimovich stadium
after the Russian mathematician who studied its properties. The path is quite irregular, in fact it's chaotic. Such models are used in mechanics.
Figure 15.7
Billiards in a hippodrome
Billiards in a hippodrome

Let's
return to Mary's puzzle and to optics, one of the earliest sciences. Heron's conclusion that rays of light reflecting off a plane mirror take the shortest possible path suggests Aristotle
's claim that ‘Nature does nothing in vain’,
[Aristotle
De Anima
III:12] which remained a popular idea among early modern scientists such as Newton who wrote:
return to Mary's puzzle and to optics, one of the earliest sciences. Heron's conclusion that rays of light reflecting off a plane mirror take the shortest possible path suggests Aristotle
's claim that ‘Nature does nothing in vain’,
[Aristotle
De Anima
III:12] which remained a popular idea among early modern scientists such as Newton who wrote:
To this purpose the philosophers say, that Nature does nothing in vain, and more is in vain, when less will serve; for Nature is pleased with simplicity, and affects not the pomp of superfluous causes.
Heron's argument successfully linked this very attractive but frankly metaphysical axiom to mathematics and to physics. However, Heron's reference to shortest distance proved mistaken. Everyone has noticed that objects, such as a stick, appear ‘bent’ when seen standing in water.
The Greeks certainly did, but not until Kepler did anyone try to explain why [Kepler
1611
]. Ten years later, Willebrord Snell did some careful experiments and concluded that the angles made by the incident and refracted rays with the normals to the surface fit
Snell's Law
(
Figure 15.8
).
1611
]. Ten years later, Willebrord Snell did some careful experiments and concluded that the angles made by the incident and refracted rays with the normals to the surface fit
Snell's Law
(
Figure 15.8
).
Figure 15.8
Snell's law
Snell's law

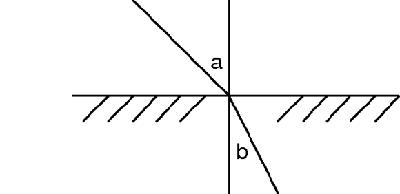
Snell's law says that if
a
is the angle between the incident light and the normal and
b
is the angle between the normal and the refracted beam, then sin
a
/sin
b
is constant.
a
is the angle between the incident light and the normal and
b
is the angle between the normal and the refracted beam, then sin
a
/sin
b
is constant.
This is an elegant result but it contradicts Aristotle's claim, which upset Fermat (1601–1665). His own calculations suggested that Heron was wrong and that it was not the distance that was minimised, but the time taken. (In Heron's original problem, it makes no difference whether he minimises time or distance because the problem is reflection in one medium not refraction in two. Actually, the time can in some cases be a maximum: it is the fact that it is stationary that is crucial.) Using his corrected principle, Fermat then proved, rather to his disappointment, that Snell's law was indeed correct, giving further support to Aristotle's metaphysics.
Pierre de Maupertuis (1698–1759) was the next natural philosopher to build on Aristotle, Heron and Fermat. He gave a Christian spin to the idea that God as the creator of everything in nature and its prime mover always acted to minimise the ‘quantity of action’.
The laws of movement and of rest deduced from this principle being precisely the same as those observed in nature, we can admire the application of it to all phenomena. The movement of animals, the vegetative growth of plants…are only its consequences; and the spectacle of the universe becomes so much the grander, so much more beautiful, the worthier of its Author, when one knows that a small number of laws, most wisely established, suffice for all movements.
Maupertuis came to his principle while working, appropriately, on the theory of light, but he believed that it applied to all the laws of nature. In physics, he suggested that the quantity to be minimised ought to be the product of the time taken by the event and the
vis viva
which was twice what we would call the kinetic energy of the system. The modern
principle of least action
minimises the difference between the kinetic energy and the potential energy, summed along the path of the action.
vis viva
which was twice what we would call the kinetic energy of the system. The modern
principle of least action
minimises the difference between the kinetic energy and the potential energy, summed along the path of the action.
Ironically, recalling Newton's enthusiasm, the principle of least action provides a foundation for mechanics which is independent of Newton's laws as well as being used in the general theory of relativity and quantum mechanics. A principle that once seemed an attractive speculation has had a lasting influence on science and maths across more than 2000 years.
Other books
Just Stitches: 54 Knitting Stitch Patterns by Tara Cousins
Sally's Bones by MacKenzie Cadenhead
Shifting the Night Away by Artemis Wolffe, Cynthia Fox, Terra Wolf, Lucy Auburn, Wednesday Raven, Jami Brumfield, Lyn Brittan, Rachael Slate, Claire Ryann
Bloodstone by Gillian Philip
A Hero's Curse by P. S. Broaddus
One Hot Desert Night by Kristi Gold
Savior (The Keepers of Hell Book 1) by James, Danielle
The Playboy's Princess by Joy Fulcher
Prom and Prejudice by Stephanie Wardrop