Games and Mathematics (13 page)
Read Games and Mathematics Online
Authors: David Wells
A first conjecture is that to make the sides equal we need a mixture of small and large – but just what mixture? A more specific conjecture is that if any set of integers has what we might call the
Liouville property
, then they are the set of factors of an integer. Is this conjecture true? It seems natural, and I would – at this moment – find it very surprising if it were false, but apart from that feeling, I have no idea.
Liouville property
, then they are the set of factors of an integer. Is this conjecture true? It seems natural, and I would – at this moment – find it very surprising if it were false, but apart from that feeling, I have no idea.
Pupils who are introduced to algebra-as-a-game can appreciate that they have a choice of moves, that some moves will be better than others, that they need to look ahead, that look-ahead depends on their past experience, and that practice is required, not the skill-practice which hones a skill to perfection, but game-practice which develops their understanding of the miniature game-world.
School algebra is wrecked as a creative subject by being taught – like elementary arithmetic – as a collection of algorithms which few pupils understand, instead of being a creative and fascinating exploration of patterns and relationships, smart moves and surprising results. The following example by that great master Euler shows him, at a very high level, playing the game of algebra quite brilliantly. Not surprisingly, his
pentagonal number theorem
also illustrates the roles of perception and scientific induction: all three aspects of mathematics really are difficult to separate in practice.
pentagonal number theorem
also illustrates the roles of perception and scientific induction: all three aspects of mathematics really are difficult to separate in practice.
Euler starts by explaining that,

Euler then records that he actually multiplied out a large number of terms to get this series:
 This is a remarkable result because the coefficients here are what are called the
This is a remarkable result because the coefficients here are what are called the
generalised
pentagonal numbers. We take the pentagonal numbers [page 179] which are, 1, 5, 12, 22, 35, 51, 70…and their formula
n
(3
n
−1)/2 and we allow
n
to be negative as well as positive.
In considering the partitions of numbers, I examined, a long time ago, the expression


generalised
pentagonal numbers. We take the pentagonal numbers [page 179] which are, 1, 5, 12, 22, 35, 51, 70…and their formula
n
(3
n
−1)/2 and we allow
n
to be negative as well as positive.
The formula then gives us for
n
= 0, ±1, ±2, ±3, ±4…the sequence, 0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70…
n
= 0, ±1, ±2, ±3, ±4…the sequence, 0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70…
So far, so scientific. Euler is confident that the coefficients must be what they seem to be:
For each of us can convince himself of this truth by performing the multiplication as far as he may wish; and it seems impossible that the law which has been discovered to hold for 20 terms, for example, would not be observed in the terms that follow.
However, so far he has only
induced
his conclusion scientifically: a proof is nowhere to be seen – but Euler perseveres, with his usual imagination and flair: he ‘manoeuvred those two expressions in many ways’, he writes, his first move being to ‘[get] rid of the factors in the first by taking logarithms’.
induced
his conclusion scientifically: a proof is nowhere to be seen – but Euler perseveres, with his usual imagination and flair: he ‘manoeuvred those two expressions in many ways’, he writes, his first move being to ‘[get] rid of the factors in the first by taking logarithms’.
Calling the product
s
, he concludes that,
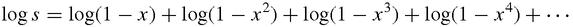 Next, ‘In order to get rid of the logarithms, I differentiate and obtain the equation’:
Next, ‘In order to get rid of the logarithms, I differentiate and obtain the equation’:
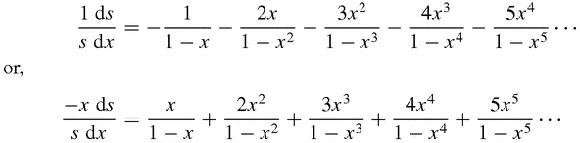 Euler, unlike most mathematicians then or now, is fully explaining his actions. His next move is to calculate the same expression (−
Euler, unlike most mathematicians then or now, is fully explaining his actions. His next move is to calculate the same expression (−
x
/
s
)d
s
/d
x
from the second equation, the series with the generalised pentagonal number coefficients, (so that he now has two ways of writing the same function), and then to go back to the expression above and expand every one of the expressions
x
/(1−
x
), 2
x
2
/(1−
x
2
)…as a geometric series. He then makes a remarkable observation which brings in the
divisors
of the exponents:
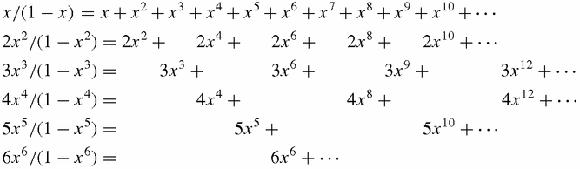 and so on…
and so on…
s
, he concludes that,
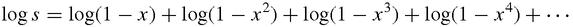
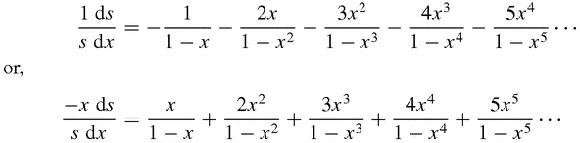
x
/
s
)d
s
/d
x
from the second equation, the series with the generalised pentagonal number coefficients, (so that he now has two ways of writing the same function), and then to go back to the expression above and expand every one of the expressions
x
/(1−
x
), 2
x
2
/(1−
x
2
)…as a geometric series. He then makes a remarkable observation which brings in the
divisors
of the exponents:
Here we easily see that each power of x arises as many times as its exponent has divisors, and that each divisor arises as a coefficient of the same power of
x
.
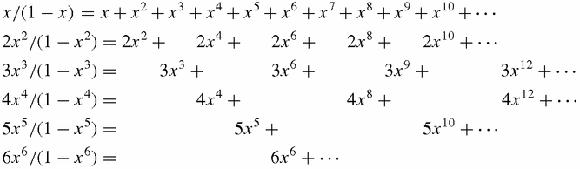
In this table,
x
6
(for example) appears four times, with the coefficients 1, 2, 3 and 6, the divisors of 6.
x
6
(for example) appears four times, with the coefficients 1, 2, 3 and 6, the divisors of 6.
It follows that, ‘if we collect the terms with like powers, the coefficient of each power of x will be the sum of the divisors of the exponent’.
Euler concludes his memoir, (we are jumping forward at this point) by
proving
a remarkable formula for the sum of divisors of an integer which he had previously inducted by scientific observation:
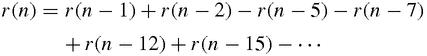 …in which the series continues until an argument is negative, with the proviso – itself remarkable – that if
…in which the series continues until an argument is negative, with the proviso – itself remarkable – that if
r
(0) appears at the end of the series, then it is counted as
n
.
proving
a remarkable formula for the sum of divisors of an integer which he had previously inducted by scientific observation:
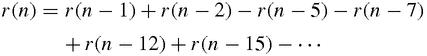
r
(0) appears at the end of the series, then it is counted as
n
.
Euler, by his original scientific observation followed by a sequence of very powerful game-like moves has found this stunning connection between the generalised pentagonal series and the sums of divisors of the integers.
His simple but powerful
manoeuvres
– as he puts it – were revealed to him by his analysis of his original position, just as any chess player analyses a position, seeking the best sequence of moves. (Unfortunately we do not know what his
unsuccessful
manoeuvres were.)
manoeuvres
– as he puts it – were revealed to him by his analysis of his original position, just as any chess player analyses a position, seeking the best sequence of moves. (Unfortunately we do not know what his
unsuccessful
manoeuvres were.)
Euler comments that ‘although we consider here the nature of integers to which the Infinitesimal Calculus does not seem to apply, nevertheless I reached my conclusion by differentiations and other devices.’ The mathematician has the advantage that he or she can switch games or develop the rules of the game, up to a point, in a way that the chess player cannot.
His brilliant game-like combinations, producing the relationship he needs in just a handful of simple powerful moves is worthy of the great Capablanca,
or of Fisher or Kasparov. Without it, or some equivalent game-like sequence, he would not have progressed beyond his scientific pattern spotting.
or of Fisher or Kasparov. Without it, or some equivalent game-like sequence, he would not have progressed beyond his scientific pattern spotting.
George Polya claimed that Euler's beautiful memoir on his pentagonal number theorem ‘is entirely devoted to the exposition of an inductive argument’. This is misleading: Polya was prejudiced by his devotion to induction. On the contrary, it is just as much an example of game-like brilliance [Polya
1954
: 96–98] [Wells
1991
b].
1954
: 96–98] [Wells
1991
b].
Is it a coincidence that Euler here combines his dazzling ability for pattern-spotting with his equal ability to play the game of mathematics brilliantly? No, rather the opposite, the two aspects go hand in hand. The theory of numbers, even more than other branches of mathematics, has been developed over centuries to a highly game-like state, in which it is both extremely easy – because it involves the integers – to generate data for scientific inductions
and
to perform formal manipulations. It is natural, therefore, that amateurs should always have found it a rich field for their modest efforts while it has also exercised the genius of the greatest masters of induction in mathematics, such as Euler, Gauss and Ramanujan, who were also among the greatest formal manipulators.
and
to perform formal manipulations. It is natural, therefore, that amateurs should always have found it a rich field for their modest efforts while it has also exercised the genius of the greatest masters of induction in mathematics, such as Euler, Gauss and Ramanujan, who were also among the greatest formal manipulators.
7
Euclid and the rules of his geometrical game
Euclid and the rules of his geometrical game
At the age of twelve I experienced a second wonder of a totally different nature: in a little book dealing with Euclidean plane geometry…Here were assertions, as for example the intersection of the three altitudes of a triangle in one point, which – though by no means evident – could nevertheless be proved with such certainty that any doubt appeared to be out of the question.This lucidity and certainty made an indescribable impression upon me.
Euclid and his
Elements
of geometry were considered for more than 2000 years to be the pinnacle and model of mathematical perfection. We now know better but the
Elements
remain an amazing achievement: so simple and so powerful despite their imperfections.
Elements
of geometry were considered for more than 2000 years to be the pinnacle and model of mathematical perfection. We now know better but the
Elements
remain an amazing achievement: so simple and so powerful despite their imperfections.
Euclid started by listing 23 definitions, 5 postulates, and 5 common notions as a foundation for the whole of geometry. Below are some of the definitions and all the postulates. The
common notions
really do seem ‘common’ and quite obvious, for example that
equals added to equals, make equals
. The postulates consists of three
actions
which Euclid assumes can always be carried out, and two assumptions. The first seems natural enough – but Euclid still felt obliged to state it – but the famous 5th postulate is by no means obvious and it was eventually discovered in the nineteenth century that if you deny it and substitute a suitable alternative you can get several perfectly consistent geometries that are non-Euclidean.
common notions
really do seem ‘common’ and quite obvious, for example that
equals added to equals, make equals
. The postulates consists of three
actions
which Euclid assumes can always be carried out, and two assumptions. The first seems natural enough – but Euclid still felt obliged to state it – but the famous 5th postulate is by no means obvious and it was eventually discovered in the nineteenth century that if you deny it and substitute a suitable alternative you can get several perfectly consistent geometries that are non-Euclidean.
Here are some of the definitions and postulates of Euclid's
Elements
:
Elements
:
DEFINITIONS1.
A point is that which has no part.2.
A line is breadthless length.3.
The extremities of a line are points.4.
A straight line is a line which lies evenly with the points on itself.5.
A surface is that which has length and breadth only.6.
The extremities of a surface are lines.10.
When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.15.
A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another;16.
And the point is called the centre of the circle.23.
Parallel lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.
POSTULATES1.
To draw a line straight from any point to any point.2.
To produce a finite straight line continuously in a straight line.3.
To describe a circle with any centre and distance [radius].4.
That all right angles are equal to one another.5.
That, if a straight line falling on two straight lines make the interior angles on the same side less than to right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than two right angles.
Let's see how Euclid developed two of his theorems. This is Book 1, Proposition 1
‘To describe an equilateral triangle upon a given finite straight line’
It's appropriate that he started Book 1 with this simple construction and that he concluded Book 13 with the construction of the five perfect Platonic solids. Greek geometry was very active as well as theoretical, it was about making constructions as well as deducing facts about geometrical figures. The Greeks called the first
problema
, and the second
theorema
. They sometimes thought that
problema
, which Euclid starts with, were simpler and easier than
theorema
[Heath
1908
: 126]. Many teachers would agree.
problema
, and the second
theorema
. They sometimes thought that
problema
, which Euclid starts with, were simpler and easier than
theorema
[Heath
1908
: 126]. Many teachers would agree.
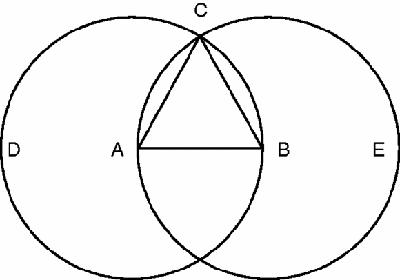
The simple solution to this
problema
is to draw two circles, each with radius equal to AB and with centres A and B (
Figure 7.1
). They intersect at C which is
the third vertex of the equilateral triangle. This is a method of constructing the equilateral triangle – and more extended patterns, including regular hexagons – that is familiar to many schoolchildren.
problema
is to draw two circles, each with radius equal to AB and with centres A and B (
Figure 7.1
). They intersect at C which is
the third vertex of the equilateral triangle. This is a method of constructing the equilateral triangle – and more extended patterns, including regular hexagons – that is familiar to many schoolchildren.
Figure 7.1
Construction of equilateral triangle
Construction of equilateral triangle

Appropriately, even in this first very elementary proposition, Euclid makes an assumption which he does not justify: he assumes that the two circles do indeed intersect. This is obvious, of course, from the diagram – but reliance on diagrams in more complicated cases can itself be misleading. Another assumption is that the circles meet in only 2 points. Yes, it's obvious, but only by looking at the figure! The very earliest commentators picked up on all these points – and others – showing the hair-splitting but invaluable obsession with proving even the smallest claim, or admitting that it's an assumption, which steered early Western mathematics towards greater and greater depth and insight.
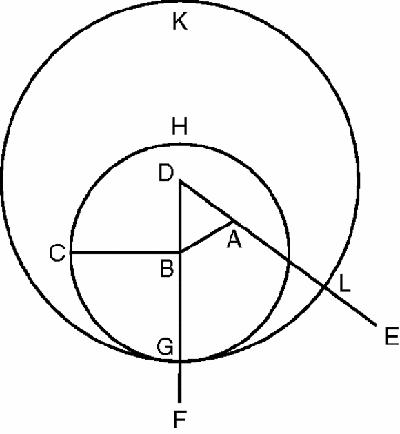
Here is Euclid's Book 1, Proposition 2, which naturally exploits Propo-sition 1:
‘From a given point, to draw a straight line equal to a given straight line.’
In
Figure 7.2
A is the given point and BC the given straight line. At first glance we might think that the obvious solution is to join A to B, and complete a parallelogram ABCD, so that AD is then equal and parallel to BC. Ah! But none of the geometrical equipment needed for that construction is yet in place. Euclid has to rely on Proposition 1 only, plus his basic axioms and postulates.
Figure 7.2
A is the given point and BC the given straight line. At first glance we might think that the obvious solution is to join A to B, and complete a parallelogram ABCD, so that AD is then equal and parallel to BC. Ah! But none of the geometrical equipment needed for that construction is yet in place. Euclid has to rely on Proposition 1 only, plus his basic axioms and postulates.
Figure 7.2
Construction of a straight line from a given point equal to a given straight line
Construction of a straight line from a given point equal to a given straight line

The solution is to join A to B and complete the equilateral triangle ABD, and extend the lines DA and DB; then draw a circle centre B and radius BC to cut DB at G, and with centre D and radius DG, draw a circle to cut DA at L. Then AL = BC.
Q.E.F
as they wrote after successful
problema
,
Quod erat faciendum
, ‘Which was to be made’, in contrast to Q.E.D,
Quod erat demonstrandum
which was written after the proof of a
theorema
.
as they wrote after successful
problema
,
Quod erat faciendum
, ‘Which was to be made’, in contrast to Q.E.D,
Quod erat demonstrandum
which was written after the proof of a
theorema
.
This is elegant, but the more complicated figure does raise a question: what if point A was in a different position relative to BC? Would the construction work perfectly? Euclid's Greek commentators handled that possibility too by drawing figures for all the possible cases they could think of.
Euclid's
Elements
is like a complex building that rises logically, one storey at a time into the sky, to be crowned with his construction of the five Platonic solids. Yet it remains only an
Elements
. Apollonius in his
Conics
went far beyond Euclid, and propositions in the
Elements
can be used to prove any number of theorems that Euclid never dreamt of. Here is one from Giovanni Ceva (1647–1734), with an ancient link.
Ceva's theoremElements
is like a complex building that rises logically, one storey at a time into the sky, to be crowned with his construction of the five Platonic solids. Yet it remains only an
Elements
. Apollonius in his
Conics
went far beyond Euclid, and propositions in the
Elements
can be used to prove any number of theorems that Euclid never dreamt of. Here is one from Giovanni Ceva (1647–1734), with an ancient link.
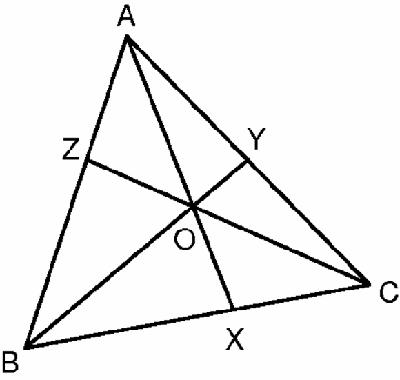
Figure 7.3
Ceva's theorem
Ceva's theorem

Yes, there is: Ceva proved that AZ/ZB · BX/XC · CY/YA = 1. The ratio AZ/ZB is the ratio of the areas of the triangles AZC and BZC, and also, similarly, of the areas of triangles AZO and BZO. But in that case, AZ/ZB is also the ratio of their differences, AOC and BOC.
Similarly, BX/XC is the ratio of BOC to COA and CY/YA is the ratio of COB to COA. So the product AZ/ZB · BX/XC · CY/YA is 1.
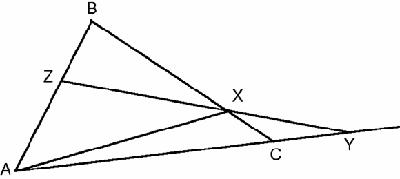
Curiously,
although Ceva's theorem is relatively modern, it strongly resembles the theorem of Menelaus
(c.70–130 CE) which says that if a line crosses the sides of a triangle (
Figure 7.4
),
Ceva's theorem is about
concurrent lines
, while Menelaus's theorem is about
collinear points
. Menelaus’ theorem also has an elegant proof. We draw a line WC parallel to YXZ (
Figure 7.5
).
although Ceva's theorem is relatively modern, it strongly resembles the theorem of Menelaus
(c.70–130 CE) which says that if a line crosses the sides of a triangle (
Figure 7.4
),
then | AY/YC · CX/XB · BZ/ZA = 1 |
concurrent lines
, while Menelaus's theorem is about
collinear points
. Menelaus’ theorem also has an elegant proof. We draw a line WC parallel to YXZ (
Figure 7.5
).
Figure 7.4
Menelaus' theorem
Menelaus' theorem

Other books
Torch (Take It Off) by Hebert, Cambria
Pleasure and a Calling by Hogan, Phil
The Beekeeper's Daughter by Santa Montefiore
Appleby File by Michael Innes
The Golden Bell by Autumn Dawn
The House of Discontent by Esther Wyndham
The Joy Luck Club by Tan, Amy
Crossed Quills by Carola Dunn
The Fragile Line: Part One (The Fine Line #2) by Alicia Kobishop
Old Bones by Aaron Elkins