Games and Mathematics (5 page)
Read Games and Mathematics Online
Authors: David Wells
2
Four abstract games


Nine Men's Morris
Hex
Four abstract games
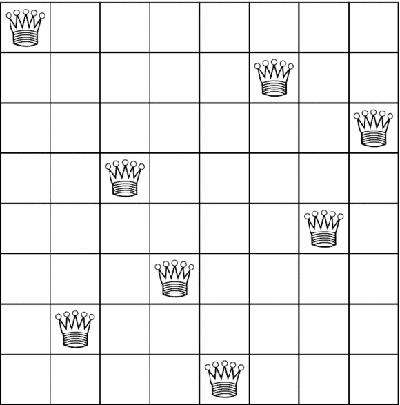
Abstract games naturally lead to puzzles and recreations such as Euler's knight tours or the Eight Queens puzzle
(
Figure 2.1
): how can eight chess queens be placed on a chessboard so that no queen attacks another?
(
Figure 2.1
): how can eight chess queens be placed on a chessboard so that no queen attacks another?
Figure 2.1
8 non-attacking queens
8 non-attacking queens

This solution looks simple, easy and elegant – but don't be fooled. There are exactly 96 solutions in total, reducing to 12 if solutions which can be rotated or reflected into each other are counted as one, and this is the only symmetrical one.
Conversely, many mathematical recreations can be turned into abstract games simply by adding suitable rules. The best-known example is Golomb's Game, created by Solomon Golomb who named and popularised pentominoes
as a recreation.
From Dudeney's puzzle to Golomb's Gameas a recreation.
The
first ‘pentomino’ puzzle was created by the great English puzzle composer Henry Ernest Dudeney (1857–1930), and published in his book,
The Canterbury Tales and other Curious Problems
[
1907
] as problem 74: The Broken Chessboard. He sets it in a lengthy medieval tale about a prince who breaks a chessboard into pieces over the head of his antagonist. The resulting pieces are the 12 pentominoes plus an extra piece 2 by 2 (Figure 2.2).
first ‘pentomino’ puzzle was created by the great English puzzle composer Henry Ernest Dudeney (1857–1930), and published in his book,
The Canterbury Tales and other Curious Problems
[
1907
] as problem 74: The Broken Chessboard. He sets it in a lengthy medieval tale about a prince who breaks a chessboard into pieces over the head of his antagonist. The resulting pieces are the 12 pentominoes plus an extra piece 2 by 2 (Figure 2.2).
Figure 2.2
12 pentominoes
12 pentominoes

Figure 2.3
Solution to Dudeney puzzle
Solution to Dudeney puzzle

The puzzle was, of course, to reassemble the original chessboard. In Dudeney's solution, Figure 2.3, the extra square piece is on the right-hand edge. Subsequently, puzzles using just the 12 pentominoes occasionally appeared, until in 1954 Solomon Golomb named them
pentominoes
in an article in
Scientific American
. He later wrote a book,
Polyominoes
(1965).
pentominoes
in an article in
Scientific American
. He later wrote a book,
Polyominoes
(1965).
To make the puzzle into a game, Golomb proposed that the players take turns to place one of the 12 pentominoes on the 8 by 8 board, without, of
course, overlapping another piece or the edges of the board. The last player to successfully place a piece is the winner.
course, overlapping another piece or the edges of the board. The last player to successfully place a piece is the winner.
The best-known abstract games have themselves many mathematical features as we shall now illustrate by looking at four examples, from the simple and extremely ancient
Nine Men's Morris
to the modern game of
Hex
, to the ancient game of
ches
s and the even older oriental game of
Go
.
Nine Men's Morris
to the modern game of
Hex
, to the ancient game of
ches
s and the even older oriental game of
Go
.
Nine Men's Morris, also known as Merelles, Muehle, Molenspel, and Mill, is a very old and simple board game, reminiscent of the children's game of tic-tac-toe or noughts-and-crosses. Boards for what appears to be Merelles have been found scratched on the walls of the Temple of Ramesses at Karnac in Egypt which dates from 1300 BCE, and the game is mentioned in Shakespeare's
A Midsummer Night's Dream
. It was popular throughout medieval Europe and is also played in China as the game of Yih. As might be expected from such an old game, the rules vary somewhat as does the size of the board and the number of pieces which might be 3 or 6 or 12 rather than 9.
A Midsummer Night's Dream
. It was popular throughout medieval Europe and is also played in China as the game of Yih. As might be expected from such an old game, the rules vary somewhat as does the size of the board and the number of pieces which might be 3 or 6 or 12 rather than 9.
Figure 2.4
Nine Men's Morris
Nine Men's Morris

The board starts empty (
Figure 2.4
) and in the first stage of the game the players take turns to place one piece at a time on a point of the board or move a piece already placed to an adjacent point, along a line, each player attempting to occupy a row of three adjacent points called a
mill
. When a mill is formed the player is allowed to capture one of his opponent's pieces which is taken off the board and never returns. (Some sets of rules disallow the capture of a piece that forms part of a mill.)
Figure 2.4
) and in the first stage of the game the players take turns to place one piece at a time on a point of the board or move a piece already placed to an adjacent point, along a line, each player attempting to occupy a row of three adjacent points called a
mill
. When a mill is formed the player is allowed to capture one of his opponent's pieces which is taken off the board and never returns. (Some sets of rules disallow the capture of a piece that forms part of a mill.)
Once all the pieces have been placed on the board, the game changes. A move now consists of moving one of your pieces from one point to an adjacent point still trying to form a mill and capture an opponent's piece. (A move which forms two mills at once, allows two of the enemy's pieces to be taken off.) At this stage, a player is allowed to move a piece out of a mill and then return
on the next move, reforming the mill and making another capturing. The game ends when one player, the loser, has only one or two pieces left.
on the next move, reforming the mill and making another capturing. The game ends when one player, the loser, has only one or two pieces left.
As abstract games go, it is very simple and in this age of computer power it has been solved completely although there are approximately 10
10
legal positions and 10
50
possible games. Ralph Gasser proved in October 1993 that with best play the game should be drawn. He also wrote a computer program called Bushy which is now the world's top player.
10
legal positions and 10
50
possible games. Ralph Gasser proved in October 1993 that with best play the game should be drawn. He also wrote a computer program called Bushy which is now the world's top player.
Nine Men's Morris
satisfies all the points we made about puzzles and recreations. It's abstract, the pieces can be anything you like and made of any material or any shape,
provided
that they are placed and move according to the rules, and you could certainly play it in your head if you had a good enough memory.
satisfies all the points we made about puzzles and recreations. It's abstract, the pieces can be anything you like and made of any material or any shape,
provided
that they are placed and move according to the rules, and you could certainly play it in your head if you had a good enough memory.
To play well you need to ‘calculate’ ahead and it also has an aesthetic quality, though that is a matter of taste like all judgements of beauty, and finally, you have to explore the game, the miniature world of Nine Men's Morris, if you want to become a competent player. It is only by exploring, conjecturing and testing that you will initially discover the
features
of the game, the best points for your first moves, the best starting sequences, and the best arrangement of pieces.
features
of the game, the best points for your first moves, the best starting sequences, and the best arrangement of pieces.
Nine Men's Morris is a world of possibilities – created entirely by its rules – but these possibilities are far richer and more complex than the rules themselves. And the rules don't tell you what possibilities follow
from
them. That is for you, the player, to discover – and it can take a very long time. With tactical sequences come very elementary proofs: you can prove by analysing the many possibilities that in certain positions one player will win whatever the second player does. We can also ask questions
about
the game: what is the shortest possible game? The longest possible? What if the size of the board were changed?
from
them. That is for you, the player, to discover – and it can take a very long time. With tactical sequences come very elementary proofs: you can prove by analysing the many possibilities that in certain positions one player will win whatever the second player does. We can also ask questions
about
the game: what is the shortest possible game? The longest possible? What if the size of the board were changed?
The Danish mathematician Piet Hein invented the game of Hex which he originally called Con-Tac-Tix in 1942 when he was a student at the Niels Bohr Institute of Theoretical Physics. He marketed it under the name of Polygon and later it become very popular in Denmark as a pen and paper game. Hein had been thinking about the Four Colour Theorem which says that a plane map can be coloured using only four colours so that no two regions with a common boundary are the same colour, and this led him to think of chains of regions.
In 1948 it was independently reinvented by a young mathematician at Princeton called John Nash, recently famous as the hero of the film
A Beautiful Mind
(2001): he was a brilliant mathematician who became schizophrenic but many years later, astonishingly, recovered and was awarded the Nobel Prize for Economics. In 1952 the games company, Parker Bros, manufactured Nash's game as Hex.
A Beautiful Mind
(2001): he was a brilliant mathematician who became schizophrenic but many years later, astonishingly, recovered and was awarded the Nobel Prize for Economics. In 1952 the games company, Parker Bros, manufactured Nash's game as Hex.
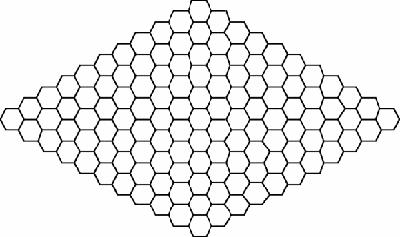
Figure 2.5
Empty Hex board, 11 by 11
Empty Hex board, 11 by 11

The board is a ‘parallelogram’ of hexagons (
Figure 2.5
), usually a rhombus, the two pairs of opposite sides being of different colours, one for each player. 11 by 11 is the commonest size but it can be played on any size at all or indeed on other shapes: it has been played on a map of States of the United States of America, with the border divided into four parts.
Figure 2.5
), usually a rhombus, the two pairs of opposite sides being of different colours, one for each player. 11 by 11 is the commonest size but it can be played on any size at all or indeed on other shapes: it has been played on a map of States of the United States of America, with the border divided into four parts.
The rules are extremely simple: the board starts empty and players take turns to place a piece of their colour on one of the empty hexagons and the winner is the player to make a chain which connects their two sides of the board.
Hex seems impossible to master. Although the rules are so simple, there are 121 first moves on a board 11 by 11, so a move-by-move tree analysis of all the possible starting sequences is prohibitive. We can say that one player must win a completed game because only a chain of one colour can completely stop a chain of the other colour being formed, as John Nash realised. He also proved in 1949 that the first player must win with best play but unfortunately he gave an
existence proof
which tells you nothing at all about the winning strategy.
existence proof
which tells you nothing at all about the winning strategy.
Also unfortunately, the first player has a very large advantage so most games are played today with the ‘swop’ rule: after the first move has been played, the second player has the option of ‘swopping’ places with the first player and accepting the move played as his first move. (This has the disadvantage of reducing the number of reasonable first moves; playing on a larger board would presumably reduce the first-move advantage.)
John Nash
favoured a larger board 14 by 14 which makes the game harder but also allows greater opportunity for strategies to appear: on very small boards, calculation alone will help you to play well and strategy hardly exists. (This is a general feature of board games: tactics dominate on small boards, strategy appears as the board gets larger.)
favoured a larger board 14 by 14 which makes the game harder but also allows greater opportunity for strategies to appear: on very small boards, calculation alone will help you to play well and strategy hardly exists. (This is a general feature of board games: tactics dominate on small boards, strategy appears as the board gets larger.)
Hex has become a favourite game among AI enthusiasts. The small 7 by 7 Hex game has been ‘solved’ by computer analysis, meaning that a winning strategy has been found: the first player plays in the centre of the board to take advantage of symmetry.
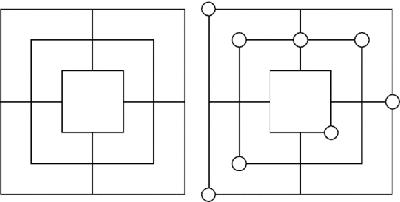
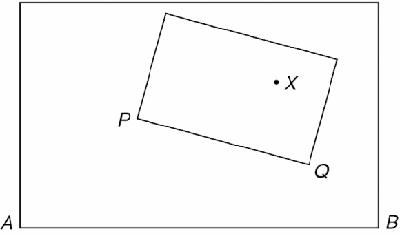
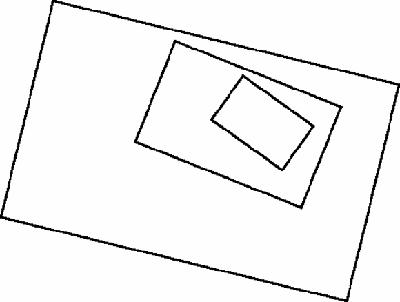
Even more than Nine Men's Morris, Hex is a highly mathematical game. In fact, it has even been used to prove
Brouwer's fixed point theorem
in pure mathematics. We can illustrate this theorem with two maps, one a small version of the other, lying on top of one another and completely overlapping (
Figure 2.6
).
Brouwer's fixed point theorem
in pure mathematics. We can illustrate this theorem with two maps, one a small version of the other, lying on top of one another and completely overlapping (
Figure 2.6
).
Figure 2.6
Overlapping maps and common point
Overlapping maps and common point

PQ corresponds to AB. The theorem says that there is a common point, X, representing the same location on both maps. (This would still be so if the top map were crumpled up into a ball instead of lying flat, but it would not be so if part of one map lay off the edge of the other.)
One way to see this is to create this sequence of maps in which each pair of maps has the same relation as the previous pair so that the maps get smaller and smaller and tend towards a limiting point which will be solution to the problem (
Figure 2.7
).
Figure 2.7
).
Figure 2.7
Sequence of repeated maps
Sequence of repeated maps

The original theorem is much harder to prove but David Gale, a fellow student with John Nash, did it by showing that it is equivalent to the theorem that the game of Hex cannot end in a draw.
The miniature world of Hex is far more complex than Nine Men's Morris so there are more tactical possibilities and strategical ideas. The board appears empty at the start but that, as always, is a kind of illusion. Although the rules and the board are amazingly simple, they still force into being a world of complex
possibilities: they don't create a world out of nothing, but out of very little, and these potential patterns and possibilities existed the moment the game was invented.
possibilities: they don't create a world out of nothing, but out of very little, and these potential patterns and possibilities existed the moment the game was invented.
Cameron Browne has written the first complete book on Hex
tactics and strategy,
Hex Strategy: Making the Right Connections
[Browne
2000
]. His use of technical terms such as
bridges
,
templates
,
spanning paths
,
ladders
,
groups
,
chains
,
edge defence
, and so on, suggests the wealth of concepts that aid the experienced player. (Browne has also published a more general book on
Connection Games
.)
tactics and strategy,
Hex Strategy: Making the Right Connections
[Browne
2000
]. His use of technical terms such as
bridges
,
templates
,
spanning paths
,
ladders
,
groups
,
chains
,
edge defence
, and so on, suggests the wealth of concepts that aid the experienced player. (Browne has also published a more general book on
Connection Games
.)
To discover these tactical and strategical ideas, however, is not easy. Many years ago while puzzle editor of
Games & Puzzles
magazine I wrote a review of
TwixT
, a proprietary variation of Hex in which pegs are connected by knight's moves, and made the mistake of presenting an annotated game without consulting the inventor, Alex Randolph, and on the basis (it became clear) of far too little experience. I had only explored TwixT very superficially. The result was embarrassing, a letter by return of post explaining why my analysis was feeble, mistaken and wrong.
Games & Puzzles
magazine I wrote a review of
TwixT
, a proprietary variation of Hex in which pegs are connected by knight's moves, and made the mistake of presenting an annotated game without consulting the inventor, Alex Randolph, and on the basis (it became clear) of far too little experience. I had only explored TwixT very superficially. The result was embarrassing, a letter by return of post explaining why my analysis was feeble, mistaken and wrong.
My illustrative game was obviously not elegant let alone beautiful but Hex is sufficiently complex to be both, though no-one has yet, to the best of my knowledge, published a collection of
X's Best Games of Hex
– but who knows, the time may come. In the meantime, interested readers might like to try the Hex problems in Cameron Browne's book.
X's Best Games of Hex
– but who knows, the time may come. In the meantime, interested readers might like to try the Hex problems in Cameron Browne's book.
Other books
Peter the Great by Robert K. Massie
The Magician's Tower by Shawn Thomas Odyssey
Offshore by Penelope Fitzgerald
See Jane Love by Debby Conrad
Alien Probe (An Erotic Short Story) by Lily, Tiger
The Young Desire It by Kenneth Mackenzie
The Ring of Death by Sally Spencer
Three Heroes by Beverley, Jo
The Guardian of My Soul (Soul's Desire) by Emily A. Lawrence