Games and Mathematics (4 page)
Read Games and Mathematics Online
Authors: David Wells
Lucas and mathematical recreations
Lucas's game of solitaire calculation
Édouard Lucas (1842–1891) was a talented French mathematician with an enthusiasm for recreations. In his
Récréations Mathématiques
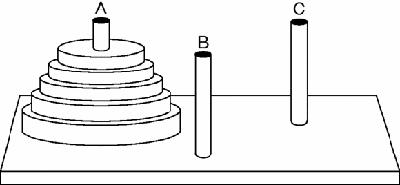
he discussed the Tower of Hanoi
, a puzzle which he invented in 1883 and published under the name, ‘N. Claus de Siam’ as, ‘A game of combination designed to explain the binary system of numeration.’ It created a sensation and was soon exploited in an advertising version, the Eight Puzzle, in which each disc advertised a different product. Lucas also made a giant version more than a metre high for public display. It is indeed a game, albeit a very simple one-person game, and it is also very mathematical. This is how it works. The object is to transfer all the rings in
Figure 1.12
from peg A to peg C, following these two simple rules:
The basic insight is that to move the 5 discs from A to C, you need to move the top 4 discs from A to B, then move the largest disc to C, and then move the
4 discs from B to C. The solution starts, naming only the number of the disc and the destination peg:
Récréations Mathématiques
he discussed the Tower of Hanoi
, a puzzle which he invented in 1883 and published under the name, ‘N. Claus de Siam’ as, ‘A game of combination designed to explain the binary system of numeration.’ It created a sensation and was soon exploited in an advertising version, the Eight Puzzle, in which each disc advertised a different product. Lucas also made a giant version more than a metre high for public display. It is indeed a game, albeit a very simple one-person game, and it is also very mathematical. This is how it works. The object is to transfer all the rings in
Figure 1.12
from peg A to peg C, following these two simple rules:
(1)
Only one ring can be moved at a time.
(2)
No ring may ever be placed on top of a smaller ring.
4 discs from B to C. The solution starts, naming only the number of the disc and the destination peg:
Figure 1.12
Tower of Hanoi puzzle
Tower of Hanoi puzzle

1 to C 2 to B 1 to B 3 to C 1 to A 2 to C 1 to C 4 to B 1 to B 2 to A 1 to A 3 to B 1 to C 2 to B 1 to B 5 to C
followed by repeating the process of getting discs 1 to 4 from B to C.
Why do we say this was so mathematical? Here are three reasons:
It is abstract
, because you can make the pieces of anything you like, and their exact dimensions don't matter. The rules refer to the
size
of the rings but you could just as well distinguish them by colour from dark to light or by numbers or by letters of the alphabet. The only crucial feature is that they are arranged in a fixed order.
•
It is abstract.
•
It can be played in the head.
•
We can
prove
our conclusions.
, because you can make the pieces of anything you like, and their exact dimensions don't matter. The rules refer to the
size
of the rings but you could just as well distinguish them by colour from dark to light or by numbers or by letters of the alphabet. The only crucial feature is that they are arranged in a fixed order.
It can be played in the head
. You might try this yourself: start with 2 discs, then 3 discs, then 4, and see how quickly and correctly you can transfer them. (There is a simple rule which tells you which empty peg the first disc should be moved to.)
. You might try this yourself: start with 2 discs, then 3 discs, then 4, and see how quickly and correctly you can transfer them. (There is a simple rule which tells you which empty peg the first disc should be moved to.)
You can prove your conclusions about it
. We have almost done this already. In order to move
N
+ 1 discs from peg A to peg C,
N
discs must be moved to peg B, the largest disc moved to peg C and the remaining disks moved from B to C. Therefore, if it takes
P
moves to move
N
discs it takes 2
P
+ 1 moves for
N
+ 1 disks. The sequence of minimum moves needed for n disks therefore starts,
The formula for
N
disks is 2
N
− 1. (Generalisations of the Tower of Hanoi are a very different matter. How many moves are needed if you have not 3 pegs but 4 or 5? If the disks are initially placed not all on one peg, but on several different pegs? These problems are much harder.)
. We have almost done this already. In order to move
N
+ 1 discs from peg A to peg C,
N
discs must be moved to peg B, the largest disc moved to peg C and the remaining disks moved from B to C. Therefore, if it takes
P
moves to move
N
discs it takes 2
P
+ 1 moves for
N
+ 1 disks. The sequence of minimum moves needed for n disks therefore starts,
disks | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
moves | 1 | 3 | 7 | 15 | 31 | 63 | 127 | 255 | 511 | … |
N
disks is 2
N
− 1. (Generalisations of the Tower of Hanoi are a very different matter. How many moves are needed if you have not 3 pegs but 4 or 5? If the disks are initially placed not all on one peg, but on several different pegs? These problems are much harder.)
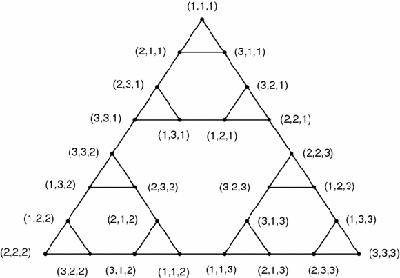
The solution we have given requires no figure or diagram, but we can if we wish represent the solution as in
Figure 1.13
. All possible moves for
3 disks are represented in the
graph
which resembles the pattern of Pascal's triangle
.
Figure 1.13
. All possible moves for
3 disks are represented in the
graph
which resembles the pattern of Pascal's triangle
.
(It is a mathematical
graph
because it consists of points or
vertices
, joined by lines: each vertex represents a position, and each line joins two positions that can be reached from each other in a single move.)
graph
because it consists of points or
vertices
, joined by lines: each vertex represents a position, and each line joins two positions that can be reached from each other in a single move.)
The notation (2,3,1) indicates that the smallest disk is on peg 2, the middle disk in peg 3 and the largest disk is on peg 1. If all three disks start on peg 1, then they can be moved to peg 2 in 7 moves by simply following the sequence down the left side of the triangle.
We could say that the original ‘physical’ puzzle and this diagram have exactly the same form or
structure
, with the difference that seeing a path from one point on the diagram to another, with the eye, is far simpler than actually making the moves of the puzzle that they represent!
structure
, with the difference that seeing a path from one point on the diagram to another, with the eye, is far simpler than actually making the moves of the puzzle that they represent!
The diagram also illustrates a crucial point that we shall meet again and again and again: the original rules of the Tower of Hanoi
puzzle are very simple and say nothing about any pattern or structure beyond the original three pegs and the disks of decreasing size. Yet as soon as we explore it we discover a
hidden structure
that is
implied
by the rules but which can only be discovered by experience, plus imagination and insight. We experience this hidden structure when we learn to solve the puzzle and the diagram then makes it visible.
puzzle are very simple and say nothing about any pattern or structure beyond the original three pegs and the disks of decreasing size. Yet as soon as we explore it we discover a
hidden structure
that is
implied
by the rules but which can only be discovered by experience, plus imagination and insight. We experience this hidden structure when we learn to solve the puzzle and the diagram then makes it visible.
One of Lucas's many interests was finding whether a given number is prime. He was the first mathematician to find tests for extremely large numbers that were much quicker to execute than dividing by all possible factors. In 1876 he showed that the enormous Mersenne number
, M
127
= 2
127
− 1 is prime by using this test.
, M
127
= 2
127
− 1 is prime by using this test.
Let p = 2
4
m
+3
−1, where 4
m
+ 3 is prime. Form the sequence
in which S
1
= 3 and S
n
+1
= S
n
2
− 2. Then
p
is prime if the smallest value of
k
such that
p
divides S
k
, is 4
m
+ 2.
4
m
+3
−1, where 4
m
+ 3 is prime. Form the sequence
3 | 7 | 47 | 2207 | 4870847…. |
1
= 3 and S
n
+1
= S
n
2
− 2. Then
p
is prime if the smallest value of
k
such that
p
divides S
k
, is 4
m
+ 2.
This test is simple in theory but requires an enormous amount of computation. How did Lucas do it by hand? With typical ingenuity he used binary arithmetic and turned the calculation into a kind of game, using a 127×127 chess board. Here is his method applied to the much simpler example of M
7
. (Readers of a nervous disposition may prefer to skip this explanation.)
7
. (Readers of a nervous disposition may prefer to skip this explanation.)
The main operation of testing involves squaring, subtracting 2, and reduction modulo 127. To perform this on S
3
to calculate S
4
, we first write S
3
in binary, as 101111. Next, we start to square it by traditional long multiplication, applied to binary:
Next, because we only need to find the answer modulo 127, and we know that 2
7+
m
= 2
m
(mod 127), so 2
7
= 2
0
, 2
8
= 2
1
, 2
9
= 2
2
, and so on, we put the lines of the long multiplication into this square array:
Lucas suggested using part of a chess board, with pawns for ones and empty squares for zeros, following these two rules:
Continue performing these operations until the only pawns remaining are in the first row. Lucas claimed that the operations of his ‘game’, with practice, could be performed extremely quickly and this was how he showed that M
127
is prime. On the other hand, it would be easy to make a mistake which no doubt explains why Lucas ever afterwards showed a slight uncertainty as to whether he really had proved the primality of M
127
.
3
to calculate S
4
, we first write S
3
in binary, as 101111. Next, we start to square it by traditional long multiplication, applied to binary:
101111 |
101111 |
–––––––––––––––––‐ |
101111 |
101111 |
101111 |
101111 |
000000 |
101111 |
7+
m
= 2
m
(mod 127), so 2
7
= 2
0
, 2
8
= 2
1
, 2
9
= 2
2
, and so on, we put the lines of the long multiplication into this square array:
No. of column | 7654321 |
0 101111 | |
101111 0 | |
01111 0 1 | |
1111 0 10 | |
000 0 000 | |
11 0 1011 |
(1)
Take (when possible but only once) a pawn away from column 2. This corresponds to subtracting 2 from the square. If a pawn never appears in column 2, then 2 must be subtracted from the final answer.
(2)
For each pair of pawns in any column, remove one from the board and move the other into the column to the left, remembering that the columns to the left of column 7 is column 1.
127
is prime. On the other hand, it would be easy to make a mistake which no doubt explains why Lucas ever afterwards showed a slight uncertainty as to whether he really had proved the primality of M
127
.
Euler's ingenuity showed that everyday puzzles and well-known games can be the basis for fascinating mathematics. Lucas's cunning transformation did the opposite – it turned an apparently forbidding calculation into something much like a simple game. In recent years mathematicians have turned their attention to many other everyday situations and given them the mathematical treatment they deserve. Have you ever said as you cut a cake, ‘I’ll cut, you choose!’? This is the simplest way to divide a cake fairly between two people so both recipients will be satisfied – but what if the cake has to be divided between three or more people? You will find the answers in the book
Cake-Cutting Algorithms
by Jack Robertson and William Webb [Robertson & Webb 1998].
Cake-Cutting Algorithms
by Jack Robertson and William Webb [Robertson & Webb 1998].
You are no doubt aware also that there is more than one way to tie a tie, from the standard schoolboy knot to the Windsor knot, favoured by the late Duke. Knots are very ancient indeed but an essential part of the modern mathematical study of topology so it can't be too surprising that two ingenious Cambridge mathematicians, Thomas Fink and Yong Mao, wrote
The 85 Ways to Tie a Tie:
the Science and Aesthetics of Tie Knots
[Fink & Mao
2001
], which peaked at #5 in the Amazon mathematics best sellers list of 2005. And if that doesn't tickle your fancy then Burkhard Polster has written the definitive
The Shoelace Book: A Mathematical Guide to the best (and Worst) Ways to Lace Your Shoes
[Polster
2006
] which comes with a pair of shoelaces so that you can do your own experiments.
The 85 Ways to Tie a Tie:
the Science and Aesthetics of Tie Knots
[Fink & Mao
2001
], which peaked at #5 in the Amazon mathematics best sellers list of 2005. And if that doesn't tickle your fancy then Burkhard Polster has written the definitive
The Shoelace Book: A Mathematical Guide to the best (and Worst) Ways to Lace Your Shoes
[Polster
2006
] which comes with a pair of shoelaces so that you can do your own experiments.
The moral is: there is fascinating mathematics in so many puzzling everyday situations and much more mathematics out there than anyone ever realised!
Figure 1.3
Unicursal by Don Lemon
Unicursal by Don Lemon

Figure 1.13
Graph of Tower of Hanoi
Graph of Tower of Hanoi

Other books
Rev by J.C. Emery
Taken by the Alpha Viking by Sara Mason
Patsy's Italian Family Cookbook by Sal Scognamillo
The Dislocated Man, Part One by Larry Donnell, Tim Greaton
Trailer Park Noir by Garton, Ray
The Prisoner of Cell 25 by Richard Paul Evans
Blackmailed by the Beast by Sam Crescent
Assignment in Brittany by Helen Macinnes
Monsieur Pamplemousse and the French Solution by Michael Bond
A Freewheelin' Time by Suze Rotolo